1 Introduction

The viscoelastic absorption causes energy loss during the wave propagation in real Earth media. The viscosity of the Earth shows obvious frequency dependence, especially for high-frequency components. The resulting serious dispersion reduces seismic resolution and causes difficulties for geological interpretation. The compensation of viscoelastic attenuation is an important issue in seismic data processing. Various seismic numerical methods in viscoelastic media (Dvorkin and Mavko 2006) have been widely used to understand the detailed characteristics of viscoelastic absorption. However, most viscoelastic numerical simulations are based on the finite-difference (FD) and finite-element (FE) methods. In this study, we develop an efficient viscoelastic boundary element method (BEM) for the study of viscoelastic absorption.

With the extensive publications in seismology (Aki and Richards 1980; Emmerich and Korn 1987; Liao and McMechan 1996; Carcione et al. 2002; Carcione 2010), the implementation of viscoelastic numerical modeling can be simply divided into two categories: complex-number velocity methods in the frequency domain and quality factor-based wave equation methods in the time domain. The time-domain methods use a series of viscous parameters (i.e., the standard linear body) to describe the medium viscosity. These methods are based on various approximate constant-Q models, such as Kelvin-Voigt model, Maxwell model, and standard linear solid model (SLS). Maxwell model cannot describe the elasticity creep, whereas Kelvin-Voigt model cannot describe the stress relaxation. The SLS model (Carcione 2007) can describe both the elasticity creep and the stress relaxation, more closely approximating the real law of seismic wave propagation in viscoelastic media. It is not easy to describe frequency-dependent attenuation coefficients and dispersion effects for the time-domain methods. To simplify the problem, the constant-Q model (Kjartansson 1979) assumes that the quality factor is a linear function of frequency.

Conventional viscoelastic FD modeling can accurately describe both the kinematics and dynamics characteristics of wave propagation, but requires huge computations and computer memories. As an efficient alternative, Varela (1993) proposes a one-way time-domain viscoelastic modeling algorithm with a higher computational efficiency, but involved in a single series expansion that is valid for bigger Q values. To reduce memory requirements, Lu and Hanyga (2004) use an intermediate variable to solve the fractional-order derivative, which causes huge computations. Chen and Holm (2004) apply a fractional Laplace operator to the calculation of viscous wavefields to improve computational efficiency. Treeby and Cox (2010) further explicitly decompose the dispersion and attenuation terms in the viscoelastic FD equation, greatly improving computational efficiency. Viscoelastic seismic imaging of viscosity acoustic media can compensate viscoelastic dispersion and attenuation and has been widely used to improve seismic imaging quality (Zhu 2014; Zhu et al. 2014).

Unlike the FD and FE methods that are characteristic of the implicit use of boundary conditions, the explicit use will lead to a category of semi-analytical methods. For example, frequency-domain BEMs (e.g., Dravinski 1982; Sánchez-Sesma and Campillo 1991; Fu and Mu 1994; Fu 2002), global generalized reflection/transmission matrices methods (Chen 1990, 1995, 1996), discrete wavenumber BEMs (Bouchon 1982; Bouchon et al. 1989; Fu and Bouchon 2004), global reflection/transmission BEMS (Ge and Chen 2007, 2008), dual reciprocity BEMs (Dehghan and shirzadi 2015; Dehghan and Safarpoor 2016), and some hybrid schemes (Moczo et al. 1997; Fu and Wu 2001) are more accurate in simulating reflection/transmission across irregular interfaces and have been widely used in seismology. Targeted at numerical wave propagation in layered viscoelastic media with an explicit use of boundary continuity conditions, an efficient alternative for full-waveform viscoelastic numerical modeling is proposed in this article by extending conventional frequency-domain BEMs to viscoelastic media.

We first transform the constant-Q acoustic wave equation into the corresponding wave integral representation with the Green’s function accounting for viscoelastic coefficients in the frequency domain. The frequency-domain BE method is used to solve the integral equation for each subregion in multilayered media, and then the boundary conditions between subregions are used to assemble the BE submatrix from each subregion into a global system of matrices. In general, the resultant global coefficient matrix is sparse and narrow banded and can be solved by an improved block Gaussian elimination method. To show the applicability of the method, we present numerical examples with viscoelastic media to study the viscoelastic effect of different Q values on wave propagation.

2 Viscoelastic integral equations for multilayered media

Seismic response \(u({\varvec{r}})\) for steady-state scalar wave propagation with a constant velocity v satisfies the following scalar Helmholtz equation

$$ \nabla^{2} u({\varvec{r}}) + k^{2} u({\varvec{r}}) = - s({\varvec{r}},\omega ), $$
(1)

where the wavenumber k = ω/v and s(r,ω) is the body force. Assuming the source point is located at r 0, the source term can be expressed as

$$s({\varvec{r}},\omega ) = S(\omega )\delta ({\varvec{r}} - {\varvec{r}}_{0} ) ,$$
(2)

where \(S(\omega )\) is the source spectrum and \(\delta ({\varvec{r}} - {\varvec{r}}_{0} )\) is the delta function.

As is well known, wave propagation simulation in the frequency domain is easy to incorporate the viscoelastic coefficient into wave equation by expressing the acoustic velocity as a plural form. The resultant viscoelastic wave equation with a complex velocity plays an attenuation role in simulating wave propagation in viscoelastic media. We use the following complex-velocity expression (Ravaut et al. 2004) for the viscoelastic wave equation,

$$\frac{1}{{\bar{v}}} = \frac{1}{v}\left[ {1 + \frac{\text{i}}{2Q}{\text{sign}}(\omega )} \right] ,$$
(3)

where i = \(\sqrt { - 1} ,\) \(\bar{v}\) is the complex velocity corresponding to the real velocity v, and Q is the quality factor.

Replacing the real velocity in Eq. (1) with the complex velocity by Eq. (3), seismic response \(u({\varvec{r}})\) for viscoelastic wave propagation satisfies the following equation

$$\nabla^{2} u({\varvec{r}}) + (1 - \alpha {\text i})k^{2} u({\varvec{r}}) = - s({\varvec{r}},\omega ) ,$$
(4)

where the attenuation coefficient \(\alpha\) can be computed by the quality factor Q. Defining the complex wavenumber as \(k_{{\alpha}} = \sqrt {\left( {1 - {\alpha}{\text i}} \right)k}\), the equation can be further compacted as

$$\nabla^{2} u({\varvec{r}}) + k_{\alpha }^{2} u({\varvec{r}}) = - s({\varvec{r}},\omega ) ,$$
(5)

Consider 2D steady-state scalar wave propagation in a homogenous region Ω bounded by an irregular boundary Γ. The seismic response \(u({\varvec{r}})\) at location r ∈ Ω can be composed of the incident wavefield f(r) and the boundary wavefield u s(r) scattered by the irregular boundary Γ

$$u\left( {\varvec{r}} \right)\text{ } = f\left( {\varvec{r}} \right)\text{ } + u^{\text s} \left( {\varvec{r}} \right).$$
(6)

The incident wavefield in the background medium can be expressed as

$$f({\varvec{r}}) = \int_{\varOmega } {s({\varvec{r^{\prime}}},\omega )G({\varvec{r}},{\varvec{r^{\prime}}})} {\text{d}}{\varvec{r^{\prime}}} = s(\omega )G({\varvec{r}},{\varvec{r}}_{0} ) ,$$
(7)

which can be given directly by the characteristics of the source in the numerical implementation. Based on the Helmholtz integral representation formulas for Eq. (1), the boundary wavefield satisfies the boundary integral equation

$$u^{\text s} ({\varvec{r}}) = \int_{\varGamma } {\left[ {G({\varvec{r}},{\varvec{r^{\prime}}})\frac{{\partial u({\varvec{r^{\prime}}})}}{\partial n} - u({\varvec{r^{\prime}}})\frac{{\partial G({\varvec{r}},{\varvec{r^{\prime}}})}}{\partial n}} \right]} {\text{d}}{\varvec{r^{\prime}}} ,$$
(8)

where \(G({\varvec{r}},{\varvec{r^{\prime}}})\) and \(\frac{{\partial G({\varvec{r}},{\varvec{r^{\prime}}})}}{\partial n}\) are the free-space Green’s functions, as the basic solution of the integral equation of displacement and stress in the background of the homogeneous viscoelastic medium, respectively. ∂/∂n denotes differentiation with respect to the outward normal of the boundary Γ. The viscoelastic Green’s function in the complex domain has the similar form as the elastic Green’s function in the real domain, that is, \(G({\varvec{r}},{\varvec{r^{\prime}}}) = {\text {iH}}_{0}^{(1)} (k_{\alpha } \left| {{\varvec{r^{\prime}}} - {\varvec{r}}} \right|)/4\) for 2D problems and \(G({\varvec{r}},{\varvec{r^{\prime}}}) = {\text{e}}^{{ik_{\alpha } \left| {{\mathbf{r^{\prime}}} - {\mathbf{r}}} \right|}} /(4\pi \left| {{\varvec{r^{\prime}}} - {\varvec{r}}} \right|)\) for 3D problems, where \({\text H}_{0}^{(1)}\) denotes the complex Hanker function.

Substituting Eqs. (7), (8) in (6) and considering the “boundary naturalization” of the integral equation (that is, a limit analysis when the “observation point” r approaches the boundary Γ and tends to coincide with the “scattering point” r′ ∈ Γ), we obtain the following boundary integral equation

$$\int\limits_{\varGamma } {\left[ {G({\varvec{r}},{\varvec{r^{\prime}}})\frac{{\partial u({\varvec{r^{\prime}}})}}{\partial n} - u({\varvec{r^{\prime}}})\frac{{\partial G({\varvec{r}},{\varvec{r^{\prime}}})}}{\partial n}} \right]{\text{d}}{\varvec{r^{\prime}}}} + S(\omega )G({\varvec{r}},{\varvec{r}}_{0} ) = \left\{ \begin{aligned} \hfill u({\varvec{r}})\quad {\varvec{r}} \in \varOmega \\ \hfill C({\varvec{r}})u({\varvec{r}})\quad {\varvec{r}} \in \varGamma \\ \hfill 0\quad {\varvec{r}} \notin \bar{\varOmega } \\ \end{aligned} \right. ,$$
(9)

where \(\bar{\varOmega }\) = Ω + Γ and the coefficient C(r) depends on the local geometry at r on Γ. C(r) = θ/2π with θ the opening angle at r in the direction of Ω. The boundary integral Eq. (9) for viscoelastic wave propagation is a Fredholm integral equation of the second kind. According to the Fredholm theorems, we can prove that the solution of Eq. (9) exists and is unique for an internal boundary value problem (all r, r′ ∈ \(\bar{\varOmega }\)) with both Neumann and Dirichlet boundary conditions. The solution is also stable because the singularity that arises when r → r′ in the Green’s function is only apparent and can be removable (Fu and Mu 1994). For numerical calculations, however, particular techniques are required for the evaluation of the weakly singular integrals, for instance, the Bouchon’s discrete wavenumber expansion of the Green’s functions (Bouchon 1982) and the analytical treatment (Fu and Mu 1994) that is based on the fact that the asymptotic behavior of the integral kernels can be exactly represented by their static counterparts.

3 Numerical discretization of the viscoelastic integral equation

In this section, the frequency-domain boundary element method is used to solve the viscoelastic boundary integral equation for a full-wave solution in multilayered media. The problem to be studied is illustrated by a multilayered viscoelastic model as shown in Fig. 1. In this model, there are M + 1 homogeneous layers over a free space, with each layer bounded by two irregular interfaces and a source embedded in arbitrary layer. For simplicity, we restrict the present study to the 2D acoustic problem (or SH problem). For instance, the elastic properties of the mth layer are described by the velocity v m , density ρ m , and attenuation coefficient a m . The seismic response u(r) satisfies the following boundary conditions: the continuities of displacement and traction across interfaces and the radiation boundary conditions imposed on the far-field behavior at infinity.

Fig. 1
figure 1

Configuration of a multilayered viscoelastic model

Full size image

The collocation method has been extensively used for numerical solutions of all types of integral equations. The numerical solution of Eq. (9) by the collocation method involves several steps. First, the discretization of Eq. (9) can be done in each layer by numerical methods such as the collocation method or weighted residual method. Then, all equations are assembled into a set of simultaneous matrix equations by using the boundary conditions of continuity for displacement and traction across all interfaces. This global matrix is sparse or narrow banded, depending on the structure of the model.

We discretize all interfaces in the mth layer into L boundary elements denoted by Γ e (e = 1, 2,…, L) resulting in a total of N nodes. In the collocation method, interpolation shape functions Φ are used so that all the variables (r, u, and ∂u/∂n) are approximated by the linear combination of their nodal values over an element Γ e defined geometrically between the nodes I 1 and I 2, for example,

$$\left\{ {\begin{aligned} u\left( \xi \right) = \sum\limits_{{l = I_{1} }}^{{I_{2} }} {u\left( {{\varvec{r}}_{l} } \right)} \Phi_{l} \left( \xi \right) \\ \frac{\partial u( \xi)}{\partial n} = \sum \limits_{{l = I_{1} }}^{{I_{2} }} t\left( {{\varvec{r}}_{l} } \right)\Phi_{l} (\xi ) \\ \end{aligned} } \right. ,$$
(10)

where ξ denotes the local coordinate of an element and t is the normal gradient of u with respect to the outward normal to the boundary. Then, Eq. (9) for i = 1 to N is transformed into

$$\mathop \sum \limits_{j = 1}^{N} \left[ {H_{ij} u\left( {{\varvec{r}}_{j} } \right) - G_{ij} t\left( {{\varvec{r}}_{j} } \right)} \right] = f({\varvec{r}}_{i} ),$$
(11)

where the coefficients H ij and G ij denote a concentrated force generated at the jth scattering point and applied at the ith observation point, which can be calculated by numerically integrating the scalar product of the Green’s function with interpolation shape functions over elements,

$$H_{ij} = \sum\limits_{e = 1}^{L} {\int\limits_{{\varGamma_{e} }} {\frac{\partial }{\partial n}} } G({\varvec{r}}_{i} ,{\varvec{r^{\prime}}}(\xi ))\varPhi_{j} (\xi ){\text{d}}{\varvec{r^{\prime}}}(\xi ) + C({\varvec{r}}_{i} )\delta_{ij} ,$$
(12)
$$G_{ij} = \mathop \sum \limits_{e = 1}^{L} \mathop \int \limits_{{\varGamma_{e} }}^{{}} G\left[ {{\varvec{r}}_{i} ,{\varvec{r^{\prime}}}\left( \xi \right)} \right] \varPhi_{j} \left( \xi \right){\text{d}}{\varvec{r}}'\left( \xi \right) ,$$
(13)

where δ ij is the Kronecker delta function. These integrals can be evaluated by the Gaussian integration algorithm.

After the discretization of Eq. (9) is done for all the layers, the resulting numerical equations are assembled into a global matrix equation by the boundary conditions of continuity for displacement and traction across all interfaces. For instance, the continuities of displacement and traction across the interface Γ m are given by

$$\left\{ {\begin{aligned} &{u_{m}^{ - } ({\varvec{r}}) = u_{m}^{ + } ({\varvec{r}})} \hfill \\ &{\frac{{\rho_{m + 1} \nu_{m + 1}^{2} t_{m}^{ - } ({\varvec{r}})}}{{(1 - \alpha_{m + 1} i)}} = - \frac{{\rho_{m + 1} \nu_{m}^{2} t_{m}^{ + } ({\varvec{r}})}}{{(1 - \alpha_{m} i)}}} \hfill \\ \end{aligned} } \right. ,$$
(14)

where “−” denotes the top side of Γ m toward the mth layer and “+” denotes the underside of Γ m toward the (m + 1)th layer. The boundary continuity condition of traction can be further compacted as

$$t_{m}^{ + } ({\varvec{r}}) = - \eta_{m} t_{m}^{ - } ({\varvec{r}}),$$

where

$$\eta_{m} = \frac{{(1 - \alpha_{m + 1} i)\rho_{m} \nu_{m}^{2} }}{{(1 - \alpha_{m} i)\rho_{m + 1} \nu_{m + 1}^{2} }}$$

After applying boundary continuity conditions to boundary integral equations, Eq. (11) can be expressed as a matrix form:

$$\left[ {\begin{array}{*{20}c} {H_{{1^{ - } 1^{ - } }} } & { - G_{{1^{ - } 1^{ - } }} } & {} & {} & {} & {} & {} & {} \\ \ldots & \ldots & \ldots & \ldots & {} & {} & {} & {} \\ \ldots & \ldots & \ldots & \ldots & {} & {} & {} & {} \\ {} & {} & {H_{{m^{ + } m^{ + } }} } & {\eta_{m} G_{{m^{ + } m^{ + } }} } & {H_{{m^{ + } (m + 1)^{ - } }} } & {G_{{m^{ + } (m + 1)^{ - } }} } & {} & {} \\ {} & {} & {H_{{(m + 1)^{ - } k^{ + } }} } & {\eta_{m} G_{{(m + 1)^{ - } m^{ + } }} } & {H_{{(m + 1)^{ - } (m + 1)^{ - } }} } & {G_{{(m + 1)^{ - } (m + 1)^{ - } }} } & {} & {} \\ {} & {} & {} & {} & \ldots & \ldots & \ldots & \ldots \\ {} & {} & {} & {} & \ldots & \ldots & \ldots & \ldots \\ {} & {} & {} & {} & {} & {} & {H_{{M^{ + } M^{ + } }} } & {\eta_{M} G_{{M^{ + } M^{ + } }} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {U_{1}^{{}} } \\ \vdots \\ \vdots \\ {U_{m}^{{}} } \\ {T_{m}^{{}} } \\ \vdots \\ \vdots \\ {T_{M}^{{}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} F \\ \vdots \\ \vdots \\ 0 \\ 0 \\ \vdots \\ \vdots \\ 0 \\ \end{array} } \right] ,$$
(15)

Equation (15) expresses wave propagation through the entire model, where the boundary coefficient submatrices are calculated by Eqs. (12), (13) and the source vector on the right side can be computed by Eq. (7). After solving the linear system of Eq. (15) for u and t at all the nodes, we can compute the seismic response at any receiving point in the medium through back substitution of Eq. (9).

In the numerical implementation, we use an improved block Gaussian elimination method to solve the matrix equation for the improvement in implementation efficiency. In seismic exploration, the source is generally located in the near-surface and receivers are deployed at the free surface. In such a case, we calculate and assemble the matrices H and G from deep to shallow to eliminate coupling data on the interface between two adjacent layers until the calculation reaches the surface. The resulting final matrix equation is then solved for u and t at all the nodes inside the surface layer. Note that the maximum memory amount required for the global coefficient matrix is limited to the total node number of the biggest layer, which saves memory and reduces computational costs. Fewer elements per wavelength will reduce the size of the resultant coefficient matrices. To improve computation speed, we adopt a variable element dimension technique in the program implementation. Since a discretization rate of three points per wavelength (Campillo 1987) is sufficient to make the numerical noise level negligible for general applications, the element dimension for each computational frequency is computed according to the medium velocity and the frequency, and then the model is automatically discretized. This improves the efficiency of the BE method.

4 Numerical examples

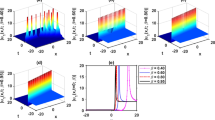
Figure 2 shows a viscoelastic homogeneous model with a velocity of 2500 m/s and three sources at different depths 1000, 2000, and 3000 m. Figure 3 shows synthetic seismograms with surface survey for Q = 10 and Q = 100, respectively. We see that the seismic resolution with Q = 100 is much better than that with Q = 10. Particularly, the synthetic amplitudes with Q = 10 decrease fast with increasing source depths, with the synthetic seismogram for the source at depth 3000 m almost invisible, whereas the synthetic amplitudes with Q = 100 decrease slowly with increasing propagation distances. The synthetic amplitudes from three sources at different depths are almost the same.

Fig. 2
figure 2

Geometry of a viscoelastic homogeneous model with three sources at different depths

Full size image
Fig. 3
figure 3

Synthetic seismograms with surface survey for Q = 10 (a) and Q = 100 (b), respectively

Full size image

To access the effect of different Q values on wave propagation, we calculate zero-offset synthetic seismograms with Q = 10, 20, 50, 100, 200, 500, and 1000, respectively. The resulting synthetic records and their frequency spectra are shown in Figs. 4, 5 and 6 for different Q values and different source depths. We see that the amplitudes decrease obviously with decreasing Q from 1000 to 10. For the same propagation distance (depth), the decrease of Q values lowers the dominant frequency and amplitude of seismograms. For the same Q value, the resulting seismograms become weaker with increasing depths. Particularly, the seismograms with Q = 10 and Q = 100 are almost invisible as shown in Fig. 6. For the seismograms with Q over 100, variations in amplitude are not significant, that is, the influence on amplitudes attenuation is small for high-enough Q values. In conclusion, these figures show a prominent influence of attenuation on wave amplitudes

Fig. 4
figure 4

Zero-offset synthetic seismograms (a) with the source at depth 1000 m and their frequency spectra (b) for different Q values

Full size image
Fig. 5
figure 5

Zero-offset synthetic seismograms (a) with the source at depth 2000 m and their frequency spectra (b) for different Q values

Full size image
Fig. 6
figure 6

Zero-offset synthetic seismograms (a) with the source at depth 3000 m and their frequency spectra (b) for different Q values

Full size image

A simple sedimentary model is shown in Fig. 7 with parameters for each layer displayed in the figure. Numerical simulations are conducted with different Q 2 values of 10, 50, 100, and 1000. Figure 8 shows the snapshots at 1000 ms for Q 2 = 10, 50, 100, and 1000, respectively. We see that the variation of Q 2 values has less effect on wave propagation for small difference in Q between layers. Otherwise, the reflection and transmission of waves are possible to reflect the variation of Q values.

Fig. 7
figure 7

Simple multilayered viscoelastic model

Full size image
Fig. 8
figure 8

Snapshots at 1000 ms of waves propagating a simple multilayered viscoelastic model with Q 2 = 10 (a), 50 (b), 100 (c), and 1000 (d)

Full size image

5 Conclusions

Most viscoelastic numerical simulations are based on the finite-difference and finite-element methods. In this article, we present an efficient alternative for full-waveform method to simulate wave propagation in multilayered viscoelastic media. First, the constant-Q acoustic wave equation is transformed into a corresponding viscoelastic integral equation in terms of viscoelastic Green functions. We then apply the conventional frequency-domain BEM to the viscoelastic integral equation for accurate viscoelastic numerical modeling. We extend the frequency-domain viscoelastic BEM to multilayered media using the boundary conditions of continuity for displacement and traction across all interfaces. The resultant global coefficient matrix is sparse and narrow banded, depending on the complexity of the model. We use an improved block Gaussian elimination method to solve the sparse matrix equation for the improvement in implementation efficiency. To improve computation speed in the program implementation, we adopt a variable element dimension technique based on the discretization rate of three points per wavelength. The element dimension for each computational frequency is computed according to the medium velocity and the frequency, and then, the model is automatically discretized. Compared to the finite-difference and finite-element methods, the viscoelastic boundary element method enjoys a distinct characteristic of the explicit use of boundary continuity conditions of displacement and traction, leading to a semi-analytical solution with sufficient accuracy for simulating the viscoelastic effect across irregular interfaces. Numerical experiments to study the viscoelastic effect of different Q values on the attenuation and dispersion of seismic waves demonstrate the accuracy and applicability of the method.