Born-series approximation to volume-scattering wave for piecewise heterogeneous media

Abstract

An efficient approximate scheme is presented for wave-propagation simulation in piecewise heterogeneous media by applying the Born-series approximation to volume-scattering waves. The numerical scheme is tested for dimensionless frequency responses to a heterogeneous alluvial valley where the velocity is perturbed randomly in the range of 5 %–25 %, compared with the full-waveform numerical solution. Then, the scheme is extended to a heterogeneous multilayered model by calculating synthetic seismograms to evaluate approximation accuracies. Numerical experiments indicate that the convergence rate of this method decreases gradually with increasing velocity perturbations. The method has a fast convergence for velocity perturbations less than 15 %. However, the convergence becomes slow drastically when the velocity perturbation increases to 20 %. The method can hardly converge for the velocity perturbation up to 25 %.

1 Introduction

The Earth consists of a system of multilayered heterogeneous media that are characterized by of large-scale irregular stratified structures and small-scale volume heterogeneities. Wave propagation in such piecewise heterogeneous media will dominate reflection/transmission effects across strong-contrast impedance boundaries. Scattering waves by small-scale volume heterogeneities lead to amplitude/phase fluctuations and wave attenuation. Such inherent piecewise heterogeneous media of the Earth challenge numerical modeling techniques being able to separate large-scale boundary-scattering waves and small-scale volume-scattering waves and subsequently to handle them separately with sufficient accuracies. Various universal numerical techniques such as finite differences and finite elements have been widely used to simulate wave propagation in such piecewise heterogeneous media. Because of the gridding discretization and an implicit use of boundary continuity conditions across interfaces, however, these methods cannot separate the boundary-scattering and volume-scattering waves and simulate them to a necessary accuracy, respectively. The explicit use of boundary continuity conditions will lead to a category of semi-analytical, semi-numerical methods (e.g., Bouchon 1982; Campillo and Bouchon 1985; Bouchon et al. 1989; Chen 1990, 1995; Fu and Wu 2001; Ge and Chen 2007, 2008). These boundary methods, for example, show a high accuracy in simulating reflection/transmission across irregular interfaces, but are limited by its ability to handle volume heterogeneities.

Some progress has been made to model piecewise heterogeneous media for integral equation numerical techniques. Fu (2002) incorporates the boundary integral representation into the Lippmann–Schwinger integral equation to model heterogeneous-layered media with irregular interfaces. The numerical method is applied to simulate widely observed strong scattered noises caused by both rugged topographies and volume heterogeneities in complex near-surface areas (Fu 2003). However, the major disadvantage of the method is associated with considerable computer-time and memory requirements because of the prohibitively expensive boundary–volume integral equation system. To handle the computational barrier, an efficient alternative is to incorporate a Born-series approximation into the boundary–volume integral equation.

The Born-series approximation, as an iterative numerical technique, has been widely used in wave propagation, scattering, and diffraction tomography. Schuster (1985a,b) and Schuster and Smith (1985) propose an elegant hybrid method for solving multibody scattering problems by incorporating a Born series and boundary integral equations, later extended to wave propagation in irregularly layered media (Schuster 1985c). In the hybrid BEM + Born-series method, the boundary integral equation matrix is perturbed into two parts, with one being inverted and the other expressed by the Born series. Yu et al. (2010a) improve the approximation method by reducing the matrix dimension by eliminating the traction field. Yu et al. (2010b) compare different BEM + Born-series modeling schemes for wave propagation in piecewise homogeneous media. For approximate solutions to the boundary–volume integral equation, Fu and Bouchon (2004) apply the Born-series approximation to the volume-scattering wave, with the boundary-scattering wave handled in a fully implicit way. The approximation is based on the fact that the volume heterogeneities within each geological formation may be relatively smooth spatially at seismic wavelengths. In the present work, we aim to establish the validity of this Born-series approximation method at seismic frequencies through comparisons with the full-waveform numerical solution (Fu 2002).

In this paper, a flexible approximate solution to the generalized Lippmann–Schwinger integral equation is investigated for wave-propagation simulation in piecewise heterogeneous media. To handle the prohibitively expensive boundary–volume integral equation system, a Born series is applied to the volume-scattering waves, leading to a Born-series approximation scheme. The approximation method is validated by dimensionless frequency responses to a heterogeneous alluvial valley with the velocity perturbed randomly in the range of 5 %–25 % and then extended to a heterogeneous multilayered model by calculating synthetic seismograms. Comparisons with the full-waveform numerical solution are made for all examples to investigate the applicability of the approximation method.

2 The generalized Lippmann–Schwinger integral equation

The generalized Lippmann–Schwinger integral equation describes wave propagation in a large-scale boundary structure with internal volume heterogeneities. It is formulated as the superposition of incident, boundary-scattering, and volume-scattering waves. The problem configuration for the jth formation Ω^(j) is depicted in Fig. 1. It is bounded by the top interface ∂Ω^(j−1) and the bottom interface ∂Ω^(j), and the side boundaries at two edges of Ω^(j) are assumed to extend to infinity. The uppermost interface ∂Ω⁽⁰⁾ is a free surface, and an arbitrary seismic source is embedded in Ω^(j). For simplicity, the present study is restricted to the 2D SH problem (or acoustic problem). The elastic properties in Ω^(j) are described by the shear modulus ${\mathit{\mu }}^{\left(j\right)}\left(\mathit{r}\right)$ and density ${\mathit{\rho }}^{\left(j\right)}\left(\mathit{r}\right)$ with the corresponding reference values μ ^(j)₀ and ρ ^(j)₀ . r = (x, z) is the position vector. The solution domain of the problem is defined as ${\overline{\mathit{\Omega }}}^{\left(j\right)}\in {\mathit{\Omega }}^{\left(j\right)}+\mathit{\partial }{\mathit{\Omega }}^{\left(j-1\right)}+\mathit{\partial }{\mathit{\Omega }}^{\left(j\right)}$.

Fig. 1

Configuration of the problem considered

Seismic response u(r) for steady-state scalar wave propagation in ${\overline{\mathit{\Omega }}}^{\left(j\right)}$ satisfies the following scalar equation.

$${\mathrm{\nabla }}^{2}u(\mathit{r})+{\left[k^{\left(j\right)}\left(\mathit{r}\right)\right]}^{2}u(\mathit{r})=-{\mathit{\delta }}_{sj}s(\mathit{r},\mathit{\omega }),\begin{array}{cc}& \mathit{r}\in {\overline{\mathit{\Omega }}}^{\left(j\right)}\\ \end{array}$$

(1)

where the wavenumber [k^(j)(r)]² = ω²ρ^(j)(r)/μ^(j)(r) with the corresponding reference wavenumber ${\left[k_0^{(j)}\right]}^2={\mathit{\omega }}^2{\mathit{\rho }}_0^{(j)}/{\mathit{\mu }}_0^{(j)},$ δ _sj = 1 for s = j and δ _sj = 0 for s ≠ j, and s(r, ω) is the body force. Supposing the source point is located at r ₀ , the source term can be expressed as $s(\mathit{r},\mathit{\omega })=S(\mathit{\omega })\mathit{\delta }\left(\mathit{r}-{\mathit{r}}_{\mathbf{0}}\right)$, where S(ω) is the source spectrum and $\mathit{\delta }\left(\mathit{r}-{\mathit{r}}_{\mathbf{0}}\right)$ is the delta distribution. Defining the relative slowness perturbation $O^{\left(j\right)}(\mathit{r})=[{\mathit{\rho }}^{\left(j\right)}\left(\mathit{r}\right){\mathit{\mu }}_0^{\left(j\right)}/\phantom{{\mathit{\rho }}^{\left(j\right)}\left(\mathit{r}\right){\mathit{\mu }}_0^{\left(j\right)}{\mathit{\rho }}_0^{\left(\text{i}\right)}{\mathit{\mu }}^{\left(j\right)}\left(\mathit{r}\right)}{\mathit{\rho }}_0^{\left(j\right)}{\mathit{\mu }}^{\left(j\right)}\left(\mathit{r}\right)]-1,$ we then rewrite Eq. (1) with respect to the reference wavenumber

$${\mathrm{\nabla }}^{2}u(\mathit{r})+{\left[k_0^{\left(j\right)}\right]}^{2}u(\mathit{r})=-{\mathit{\delta }}_{sj}S(\mathit{\omega })\mathit{\delta }\left(\mathit{r}-{\mathit{r}}_{\mathbf{0}}\right)-{\left[k_0^{\left(j\right)}\right]}^2{O}^{\left(j\right)}\left(\mathit{r}\right)u(\mathit{r})$$

(2)

With the aid of the free-space Green’s function, Eq. (2) can be transformed into the following generalized Lipmann–Schwinger integral equation

$$\begin{array}{c}\underset{\mathit{\partial }{\mathit{\Omega }}^{\left(j-1\right)}}{\int }\left[G^{\left(j\right)}(\mathit{r}\mathbf{,}{\mathit{r}}^{\mathbf{\prime }})t^{\left(j-1\right)}({\mathit{r}}^{\mathbf{\prime }})-u^{\left(j-1\right)}({\mathit{r}}^{\mathbf{\prime }})\frac{\mathit{\partial }{G}^{\left(j\right)}(\mathit{r}\mathbf{,}{\mathit{r}}^{\mathbf{\prime }})}{\mathit{\partial }n}\right]\text{d}{\mathit{r}}^{\mathbf{\prime }}+\underset{\mathit{\partial }{\mathit{\Omega }}^{\left(j\right)}}{\int }\left[G^{\left(j\right)}(\mathit{r}\mathbf{,}{\mathit{r}}^{\mathbf{\prime }})t^{\left(j\right)}({\mathit{r}}^{\mathbf{\prime }})-u^{\left(j\right)}({\mathit{r}}^{\mathbf{\prime }})\frac{\mathit{\partial }{G}^{\left(j\right)}(\mathit{r}\mathbf{,}{\mathit{r}}^{\mathbf{\prime }})}{\mathit{\partial }n}\right]\text{d}{\mathit{r}}^{\mathbf{\prime }}\\ +{\left[k_0^{\left(j\right)}\right]}^2\underset{{\mathit{\Omega }}^{\left(j\right)}}{\int }{O}^{\left(j\right)}({\mathit{r}}^{\mathbf{\prime }})w^{\left(j\right)}({\mathit{r}}^{\mathbf{\prime }})G^{\left(j\right)}(\mathit{r}\mathbf{,}{\mathit{r}}^{\mathbf{\prime }})\text{d}{\mathit{r}}^{\mathbf{\prime }}+{\mathit{\delta }}_{sj}\underset{{\mathit{\Omega }}^{(j)}}{\int }{s}^{\left(j\right)}\left({\mathit{r}}^{\mathbf{\prime }},\mathit{\omega }\right)G^{\left(j\right)}\left(\mathit{r},{\mathit{r}}^{\mathbf{\prime }}\right)\text{d}{\mathit{r}}^{\mathbf{\prime }}=\left\{\begin{array}{cc}{w}^{(j)}(\mathit{r})\hfill & \mathit{r}\in {\mathit{\Omega }}^{\left(j\right)}\hfill \\ C^{\left(j-1\right)}(\mathit{r})u^{\left(j-1\right)}(\mathit{r})\hfill & \mathit{r}\in \mathit{\partial }{\mathit{\Omega }}^{\left(j-1\right)}\hfill \\ C^{\left(j\right)}(\mathit{r})u^{\left(j\right)}(\mathit{r})\hfill & \mathit{r}\in \mathit{\partial }{\mathit{\Omega }}^{\left(j\right)}\hfill \\ 0\hfill & \mathit{r}\notin {\overline{\mathit{\Omega }}}^{\left(j\right)}\hfill \\ \hfill \end{array}\right.\\ \end{array}$$

(3)

for all ${\mathit{r}}^{\mathbf{\prime }}\in {\overline{\mathit{\Omega }}}^{(j)}$, where $u^{\left(j\right)}(\mathit{r})$ is the displacement on the boundary ∂Ω^(j), $t^{\left(j\right)}(\mathit{r})$ is the normal gradient of $u^{\left(j\right)}(\mathit{r})$ with respect to the outward normal to ∂Ω^(j), the coefficients C(r) generally depends on the local geometry at r.

In the generalized Lippmann–Schwinger integral (GLSI) equation, all the integral kernels are related to the Green’s function in the background medium, which avoids the necessity of the Green’s function of a heterogeneous medium. The causal Green’s function is defined everywhere in the free space, relating an observation point $\mathit{r}$ to a scattering point ${\mathit{r}}^{\prime }.$ It satisfies the homogeneous Helmholtz equation in the reference medium:

$${\mathrm{\nabla }}^2{G}^{\left(j\right)}\left(\mathit{r}\mathbf{,}{\mathit{r}}^{\mathbf{\prime }}\right)+{\left[k_0^{\left(j\right)}\right]}^2{G}^{\left(j\right)}\left(\mathit{r}\mathbf{,}{\mathit{r}}^{\mathbf{\prime }}\right)=-\mathit{\delta }(\mathit{r}-{\mathit{r}}^{\mathbf{\prime }}),\mathit{r},{\mathit{r}}^{\mathbf{\prime }}\in {\overline{\mathit{\Omega }}}^{\left(j\right)}.$$

(4)

For 2D problems, the Green’s function is given by (Abramowitz and Stegun 1968)

$$G^{\left(j\right)}(\mathit{r}\mathbf{,}{\mathit{r}}^{\mathbf{\prime }})=\frac{\text{i}}{4}{H}_0^{\left(1\right)}\left(k_0^{\left(j\right)}\left|{\mathit{r}}^{\mathbf{\prime }}-\mathit{r}\right|\right),$$

(5)

where $\text{i}=\sqrt{-1}$ and $H_0^{(1)}$ denotes the Hankel function of the first kind and of zeroth order.

The numerical implementation is performed in the frequency domain. The discretization of Eq. (3) can be done in each layer by the collocation method (Russell and Shampine 1972), and then all equations are assembled into a set of simultaneous matrix equations using the boundary conditions of continuity for displacement and traction across all interfaces:

$$\left\{\begin{array}{c}{u}_{-}^{\left(j\right)}(\mathit{r})=u_{+}^{\left(j\right)}(\mathit{r})\hfill \\ {\mathit{\mu }}^{\left(j\right)}\frac{\mathit{\partial }{u}_{-}^{\left(j\right)}(\mathit{r})}{\mathit{\partial }n}={\mathit{\mu }}^{\left(j+1\right)}\frac{\mathit{\partial }{u}_{+}^{\left(j\right)}(\mathit{r})}{\mathit{\partial }n}\hfill \\ \hfill \end{array}\right.\begin{array}{cc},& \\ \end{array}\mathit{r}\in \mathit{\partial }{\mathit{\Omega }}^{\left(j\right)},$$

(6)

where ‘−’ denotes the top side of ∂Ω^(j) toward Ω^(j) and ‘+’ denotes the underside of ∂Ω^(j) toward Ω^(j+1). If the domain Ω^(j) is divided into M^(j) finite elements and the boundary ∂Ω^(j) is discretized into L^(j) boundary elements, the following equation in the matrix form is obtained numerically from Eq. (3)

$${\mathit{H}}^{\left(j,1\right)}{\mathit{u}}^{(j-1)}-{\mathit{G}}^{\left(j,1\right)}{\mathit{t}}^{(j-1)}+{\mathit{H}}^{\left(j,2\right)}{\mathit{u}}^{(j)}-{\mathit{G}}^{\left(j,2\right)}{\mathit{t}}^{(j)}={\mathit{p}}^{\left(j\right)}{\mathit{w}}^{\left(j\right)}+{\mathit{\delta }}_{sj}\mathit{f},$$

(7)

where f is the incident field, ${\mathit{H}}^{\left(j,1\right)}$ and ${\mathit{G}}^{\left(j,1\right)}$ are the top-boundary coefficient matrices, ${\mathit{H}}^{\left(j,2\right)}$ and ${\mathit{G}}^{\left(j,2\right)}$ are the bottom-boundary coefficient matrices, and ${\mathit{p}}^{\left(j\right)}$ is the perturbation-domain coefficient matrix.

Equation (7) can be further compacted as a matrix equation

$${\mathit{D}}^{\left(j,1\right)}{\mathit{q}}^{\left(j-1\right)}+{\mathit{D}}^{\left(j,2\right)}{\mathit{q}}^{\left(j\right)}+{\mathit{P}}^{\left(j\right)}{\mathit{w}}^{\left(j\right)}={\mathit{\delta }}_{sj}\mathit{f},$$

(8)

where we define the boundary coefficient matrices ${\mathit{D}}^{\left(j,1\right)}=\left[{\mathit{H}}^{\left(j,1\right)};-{\mathit{G}}^{\left(j,1\right)}\right]$ and ${\mathit{D}}^{\left(j,2\right)}=\left[{\mathit{H}}^{\left(j,2\right)};-{\mathit{G}}^{\left(j,2\right)}\right]$, ${\mathit{P}}^{\left(j\right)}=\left[-{\mathit{p}}^{\left(j\right)}\right]$, and the unknown boundary displacement-traction vector ${\mathit{q}}^{\left(j\right)}=\left[{\mathit{u}}^{\left(j\right)};{\mathit{t}}^{\left(j\right)}\right]$.

We assume that the medium below the layer Ω^(N) is homogeneous, bounded by ∂Ω^(N) and a spherical surface with its radius approaching infinity. Letting the source is located in the shallowest layer Ω⁽¹⁾ as the case in seismic exploration, we can use Eq. (8) to build the following global matrix equation that describes wave propagation in the whole model

$$\left\{\begin{array}{c}{\mathit{D}}^{\left(N+1,1\right)}{\mathit{q}}^{\left(N\right)}=0\hfill \\ {\mathit{D}}^{\left(N,1\right)}{\mathit{q}}^{\left(N-1\right)}+{\mathit{D}}^{\left(N,2\right)}{\mathit{q}}^{\left(N\right)}+{\mathit{P}}^{\left(N\right)}{\mathit{w}}^{\left(N\right)}=0\hfill \\ ⋮\hfill \\ {\mathit{D}}^{\left(j,1\right)}{\mathit{q}}^{\left(j-1\right)}+{\mathit{D}}^{\left(j,2\right)}{\mathit{q}}^{\left(j\right)}+{\mathit{P}}^{\left(j\right)}{\mathit{w}}^{\left(j\right)}=0\hfill \\ {\mathit{D}}^{\left(j-1,1\right)}{\mathit{q}}^{\left(j-2\right)}+{\mathit{D}}^{\left(j-1,2\right)}{\mathit{q}}^{\left(j-1\right)}+{\mathit{P}}^{\left(j-1\right)}{\mathit{w}}^{\left(j-1\right)}=0.\hfill \\ ⋮\hfill \\ {\mathit{D}}^{\left(2,1\right)}{\mathit{q}}^{\left(1\right)}+{\mathit{D}}^{\left(2,2\right)}{\mathit{q}}^{\left(2\right)}+{\mathit{P}}^{\left(2\right)}{\mathit{w}}^{\left(2\right)}=0\hfill \\ {\mathit{D}}^{\left(1,2\right)}{\mathit{q}}^{\left(1\right)}+{\mathit{P}}^{\left(1\right)}{\mathit{w}}^{\left(1\right)}=\mathit{f}\hfill \\ \hfill \end{array}\right.$$

(9)

We see that these matrix equations are coupled in the manner of Markovian chain due to the continuity of the displacement-traction vector across interfaces. Solving the linear equation system of Eq. (9) results in seismic responses u(r) for all nodes in the medium. The Gaussian elimination algorithms can be used for small-scale problems. For large-scale problems or models with complex geometry, the resultant total coefficient matrix is sparse and the corresponding equation can be solved by an improved block Gaussian elimination algorithm if seismic survey is set at the surface (Fu 2002). Since numerous matrix operations are involved and the matrix for each frequency component must be inverted, the numerical methods are computationally intensive at high frequencies. To reduce computing time and memory, a Born-series approximation for volume-scattering wave is formulated and qualified in the following section.

3 Born-series approximation solutions for volume integral equation

The generalized Lipmann-Schwinger integral equation can be rewritten for $\mathit{r}\in {\mathit{\Omega }}^{\left(j\right)}$

$$w^{\left(j\right)}(\mathit{r})=u_0^{\left(j\right)}(\mathit{r})+u_1^{\left(j\right)}(\mathit{r})+u_2^{\left(j\right)}(\mathit{r})+{\left[k_0^{\left(j\right)}\right]}^2\underset{{\mathit{\Omega }}^{\left(j\right)}}{\int }{O}^{\left(j\right)}({\mathbf{r}}^{\prime })w^{\left(j\right)}({\mathit{r}}^{\mathbf{\prime }})G^{\left(j\right)}(\mathit{r},{\mathit{r}}^{\mathbf{\prime }})\text{d}{\mathit{r}}^{\mathbf{\prime }}.$$

(10)

Letting $f^{\left(j\right)}(\mathit{r})=u_0^{\left(j\right)}(\mathit{r})+u_1^{\left(j\right)}(\mathit{r})+u_2^{\left(j\right)}(\mathit{r}),$${\mathit{\kappa }}^{\left(j\right)}\left(\mathit{r}\mathbf{,}{\mathit{r}}^{\mathbf{\prime }}\right)=G^{\left(j\right)}\left(\mathit{r}\mathbf{,}{\mathit{r}}^{\mathbf{\prime }}\right)O^{\left(j\right)}\left({\mathit{r}}^{\mathbf{\prime }}\right),$ and λ^(j) = [k ^(j)₀ ]², we obtain

$$w^{\left(j\right)}(\mathit{r})=f^{\left(j\right)}(\mathit{r})+{\mathit{\lambda }}^{\left(j\right)}\underset{{\mathit{\Omega }}^{\left(j\right)}}{\int }{\mathit{\kappa }}^{\left(j\right)}(\mathit{r},{\mathit{r}}^{\mathbf{\prime }})w^{\left(j\right)}({\mathit{r}}^{\mathbf{\prime }})\text{d}{\mathit{r}}^{\prime }$$

(11)

We define an integral operator K^(j) by

$$K^{\left(j\right)}{w}^{\left(j\right)}(\mathit{r})=\underset{{\mathit{\Omega }}^{\left(j\right)}}{\int }{\mathit{\kappa }}^{\left(j\right)}(\mathit{r},{\mathit{r}}^{\mathbf{\prime }})w^{\left(j\right)}({\mathit{r}}^{\mathbf{\prime }})\text{d}{\mathit{r}}^{\mathbf{\prime }}\begin{array}{cc},& \mathit{r}\in \\ \end{array}{\mathit{\Omega }}^{\left(j\right)}.$$

(12)

In operator form, Eq. (11) can be rewritten

$$w^{\left(j\right)}=f^{\left(j\right)}+{\mathit{\lambda }}^{\left(j\right)}{K}^{\left(j\right)}{w}^{\left(j\right)}.$$

(13)

Equation (13) can be approximated by the Born series (Fu and Bouchon 2004)

$$w^{\left(j\right)}=\sum _{n=0}^{\infty }{\left[{\mathit{\lambda }}^{\left(j\right)}\right]}^n{\left[K^{\left(j\right)}\right]}^n{f}^{\left(j\right)}$$

(14)

For simplicity, we take a heterogeneous three-layered medium for example. We assume that there are three layers (Ω^(j), j = 1, 2, 3) in the model and the source is located in the shallowest layer Ω⁽¹⁾ as the case in seismic exploration. The shallowest layer Ω⁽¹⁾ is heterogeneous, and the other layers are still homogeneous. Then, we can use Eq. (7) to build the following global matrix equation that describes wave propagation in the whole model

$$\left|\begin{array}{cccccc}{\mathit{P}}_{\mathbf{I},\mathbf{I}}^{\mathbf{1}}& {\mathit{H}}_{\mathbf{I},\mathbf{1}}^{\mathbf{1}}& {\mathit{H}}_{\mathbf{I},\mathbf{2}}^{\mathbf{1}}& -{\mathit{G}}_{\mathbf{I},\mathbf{2}}^{\mathbf{1}}& \mathbf{0}& \mathbf{0}\\ {\mathit{P}}_{\mathbf{1},\mathbf{I}}^{\mathbf{1}}& {\mathit{H}}_{\mathbf{1},\mathbf{1}}^{\mathbf{1}}& {\mathit{H}}_{\mathbf{1},\mathbf{2}}^{\mathbf{1}}& -{\mathit{G}}_{\mathbf{1},\mathbf{2}}^{\mathbf{1}}& \mathbf{0}& \mathbf{0}\\ {\mathit{P}}_{\mathbf{2},\mathbf{I}}^{\mathbf{1}}& {\mathit{H}}_{\mathbf{2},\mathbf{1}}^{\mathbf{1}}& {\mathit{H}}_{\mathbf{2},\mathbf{2}}^{\mathbf{1}}& -{\mathit{G}}_{\mathbf{2},\mathbf{2}}^{\mathbf{1}}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& {\mathit{H}}_{\mathbf{2},\mathbf{2}}^{\mathbf{2}}& -{\mathit{G}}_{\mathbf{2},\mathbf{2}}^{\mathbf{2}}& {\mathit{H}}_{\mathbf{2},\mathbf{3}}^{\mathbf{2}}& -{\mathit{G}}_{\mathbf{2},\mathbf{3}}^{\mathbf{2}}\\ \mathbf{0}& \mathbf{0}& {\mathit{H}}_{\mathbf{3},\mathbf{2}}^{\mathbf{2}}& -{\mathit{G}}_{\mathbf{3},\mathbf{2}}^{\mathbf{2}}& {\mathit{H}}_{\mathbf{3},\mathbf{3}}^{\mathbf{2}}& -{\mathit{G}}_{\mathbf{3},\mathbf{3}}^{\mathbf{2}}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& {\mathit{H}}_{\mathbf{3},\mathbf{3}}^{\mathbf{3}}& -{\mathit{G}}_{\mathbf{3},\mathbf{3}}^{\mathbf{3}}\\ \end{array}\right|\left|\begin{array}{c}{\mathit{w}}_{\mathbf{I}}\\ {\mathit{u}}_{\mathbf{1}}\\ {\mathit{u}}_{\mathbf{2}}\\ {\mathit{t}}_{\mathbf{2}}\\ {\mathit{u}}_{\mathbf{3}}\\ {\mathit{t}}_{\mathbf{3}}\\ \end{array}\right|=\left|\begin{array}{c}{\mathit{f}}_{\mathbf{I}}\\ {\mathit{f}}_{\mathbf{1}}\\ {\mathit{f}}_{\mathbf{2}}\\ \mathbf{0}\\ \mathbf{0}\\ \mathbf{0}\\ \end{array}\right|.$$

(15)

Using the first Born approximation, w _I can be expressed as

$$w_{\text{I}}^{(1)}=f_{\text{I}}+H_{\text{I},1}{u}_1+H_{\text{I},2}{u}_2-G_{\text{I},2}{t}_2.$$

(16)

Substituting in Eq. (15), we have

$$\left|\begin{array}{ccccc}{\mathit{H}}_{\mathbf{1},\mathbf{1}}^{\mathbf{1}}{\mathbf{+}\mathit{P}}_{\mathbf{1},\mathbf{I}}^{\mathbf{1}}{\mathit{H}}_{\mathbf{I},\mathbf{1}}^{\mathbf{1}}& {\mathit{H}}_{\mathbf{1},\mathbf{2}}^{\mathbf{1}}{\mathbf{+}\mathit{P}}_{\mathbf{1},\mathbf{I}}^{\mathbf{1}}{\mathit{H}}_{\mathbf{I},\mathbf{2}}^{\mathbf{1}}& -{\mathit{G}}_{\mathbf{1},\mathbf{2}}^{\mathbf{1}}-{\mathit{P}}_{\mathbf{1},\mathbf{I}}^{\mathbf{1}}{\mathit{G}}_{\mathbf{I},\mathbf{2}}^{\mathbf{1}}& \mathbf{0}& \mathbf{0}\\ {\mathit{H}}_{\mathbf{2},\mathbf{1}}^{\mathbf{1}}{\mathbf{+}\mathit{P}}_{\mathbf{2},\mathbf{I}}^{\mathbf{1}}{\mathit{H}}_{\mathbf{I},\mathbf{1}}^{\mathbf{1}}& {\mathit{H}}_{\mathbf{2},\mathbf{2}}^{\mathbf{1}}{\mathbf{+}\mathit{P}}_{\mathbf{2},\mathbf{I}}^{\mathbf{1}}{\mathit{H}}_{\mathbf{I},\mathbf{2}}^{\mathbf{1}}& -{\mathit{G}}_{\mathbf{2},\mathbf{2}}^{\mathbf{1}}-{\mathit{P}}_{\mathbf{2},\mathbf{I}}^{\mathbf{1}}{\mathit{G}}_{\mathbf{I},\mathbf{2}}^{\mathbf{1}}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\mathit{H}}_{\mathbf{2},\mathbf{2}}^{\mathbf{2}}& -{\mathit{G}}_{\mathbf{2},\mathbf{2}}^{\mathbf{2}}& {\mathit{H}}_{\mathbf{2},\mathbf{3}}^{\mathbf{2}}& -{\mathit{G}}_{\mathbf{2},\mathbf{3}}^{\mathbf{2}}\\ \mathbf{0}& {\mathit{H}}_{\mathbf{3},\mathbf{2}}^{\mathbf{2}}& -{\mathit{G}}_{\mathbf{3},\mathbf{2}}^{\mathbf{2}}& {\mathit{H}}_{\mathbf{3},\mathbf{3}}^{\mathbf{2}}& -{\mathit{G}}_{\mathbf{3},\mathbf{3}}^{\mathbf{2}}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& {\mathit{H}}_{\mathbf{3},\mathbf{3}}^{\mathbf{3}}& -{\mathit{G}}_{\mathbf{3},\mathbf{3}}^{\mathbf{3}}\\ \end{array}\right|\left|\begin{array}{c}{\mathit{u}}_{\mathbf{1}}\\ {\mathit{u}}_{\mathbf{2}}\\ {\mathit{t}}_{\mathbf{2}}\\ {\mathit{u}}_{\mathbf{3}}\\ {\mathit{t}}_{\mathbf{3}}\\ \end{array}\right|=\left|\begin{array}{c}{\mathit{f}}_{\mathbf{1}}-{\mathit{P}}_{\mathbf{1},\mathbf{I}}^{\mathbf{1}}{\mathit{f}}_{\mathbf{I}}\\ {\mathit{f}}_{\mathbf{2}}-{\mathit{P}}_{\mathbf{2},\mathbf{I}}^{\mathbf{1}}{\mathit{f}}_{\mathbf{I}}\\ \mathbf{0}\\ \mathbf{0}\\ \mathbf{0}\\ \end{array}\right|$$

(17)

.

For the second Born approximation, w_I can be represented as

$$w_{\text{I}}^{(2)}=f_{\text{I}}+H_{\text{I},1}{u}_1+H_{\text{I},2}{u}_2-G_{\text{I},2}{t}_2+P\left(f_{\text{I}}+H_{\text{I},1}{u}_1+H_{\text{I},2}{u}_2-G_{\text{I},2}{t}_2\right)$$

(18)

We can obtain

$$\left|\begin{array}{ccccc}{\mathit{H}}_{\mathbf{1},\mathbf{1}}^{\mathbf{1}}{\mathbf{+}\mathit{P}}_{\mathbf{1},\mathbf{I}}^{\mathbf{1}}{(\mathbf{1}+\mathit{P}}_{\mathbf{1},\mathbf{I}}^{\mathbf{1}}{\mathbf{)}\mathit{H}}_{\mathbf{I},\mathbf{1}}^{\mathbf{1}}& {\mathit{H}}_{\mathbf{1},\mathbf{2}}^{\mathbf{1}}{\mathbf{+}\mathit{P}}_{\mathbf{1},\mathbf{I}}^{\mathbf{1}}{(\mathbf{1}+\mathit{P}}_{\mathbf{1},\mathbf{I}}^{\mathbf{1}}{\mathbf{)}\mathit{H}}_{\mathbf{I},\mathbf{2}}^{\mathbf{1}}& -{\mathit{G}}_{\mathbf{1},\mathbf{2}}^{\mathbf{1}}-{\mathit{P}}_{\mathbf{1},\mathbf{I}}^{\mathbf{1}}{(\mathbf{1}+\mathbf{P}}_{\mathbf{1},\mathbf{I}}^{\mathbf{1}}{\mathbf{)}\mathit{G}}_{\mathbf{I},\mathbf{2}}^{\mathbf{1}}& \mathbf{0}& \mathbf{0}\\ {\mathit{H}}_{\mathbf{2},\mathbf{1}}^{\mathbf{1}}{\mathbf{+}\mathit{P}}_{\mathbf{2},\mathbf{I}}^{\mathbf{1}}{(\mathbf{1}+\mathbf{P}}_{\mathbf{2},\mathbf{I}}^{\mathbf{1}}{\mathbf{)}\mathit{H}}_{\mathbf{I},\mathbf{1}}^{\mathbf{1}}& {\mathit{H}}_{\mathbf{2},\mathbf{2}}^{\mathbf{1}}{\mathbf{+}\mathit{P}}_{\mathbf{2},\mathbf{I}}^{\mathbf{1}}{(\mathbf{1}+\mathbf{P}}_{\mathbf{2},\mathbf{I}}^{\mathbf{1}}{\mathbf{)}\mathit{H}}_{\mathbf{I},\mathbf{2}}^{\mathbf{1}}& -{\mathit{G}}_{\mathbf{2},\mathbf{2}}^{\mathbf{1}}-{\mathit{P}}_{\mathbf{2},\mathbf{I}}^{\mathbf{1}}{(\mathbf{1}+\mathit{P}}_{\mathbf{2},\mathbf{I}}^{\mathbf{1}}{\mathbf{)}\mathit{G}}_{\mathbf{I},\mathbf{2}}^{\mathbf{1}}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\mathit{H}}_{\mathbf{2},\mathbf{2}}^{\mathbf{2}}& -{\mathit{G}}_{\mathbf{2},\mathbf{2}}^{\mathbf{2}}& {\mathit{H}}_{\mathbf{2},\mathbf{3}}^{\mathbf{2}}& -{\mathit{G}}_{\mathbf{2},\mathbf{3}}^{\mathbf{2}}\\ \mathbf{0}& {\mathit{H}}_{\mathbf{3},\mathbf{2}}^{\mathbf{2}}& -{\mathit{G}}_{\mathbf{3},\mathbf{2}}^{\mathbf{2}}& {\mathit{H}}_{\mathbf{3},\mathbf{3}}^{\mathbf{2}}& -{\mathit{G}}_{\mathbf{3},\mathbf{3}}^{\mathbf{2}}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& {\mathit{H}}_{\mathbf{3},\mathbf{3}}^{\mathbf{3}}& -{\mathit{G}}_{\mathbf{3},\mathbf{3}}^{\mathbf{3}}\\ \end{array}\right|\left|\begin{array}{c}{\mathit{u}}_{\mathbf{1}}\\ {\mathit{u}}_{\mathbf{2}}\\ {\mathit{t}}_{\mathbf{2}}\\ {\mathit{u}}_{\mathbf{3}}\\ {\mathit{t}}_{\mathbf{3}}\\ \end{array}\right|=\left|\begin{array}{c}{\mathit{f}}_{\mathbf{1}}-{\mathit{P}}_{\mathbf{1},\mathbf{I}}^{\mathbf{1}}{(\mathbf{1}+\mathbf{P}}_{\mathbf{1},\mathbf{I}}^{\mathbf{1}}{\mathbf{)}\mathit{f}}_{\mathbf{I}}\\ {\mathit{f}}_{\mathbf{2}}-{\mathit{P}}_{\mathbf{2},\mathbf{I}}^{\mathbf{1}}{(\mathbf{1}+\mathbf{P}}_{\mathbf{2},\mathbf{I}}^{\mathbf{1}}{\mathbf{)}\mathit{f}}_{\mathbf{I}}\\ \mathbf{0}\\ \mathbf{0}\\ \mathbf{0}\\ \end{array}\right|$$

(19)

.

For the nth Born approximation, w _I can be expressed as

$$w_{\text{I}}^{\left(n\right)}=\sum _{j=1}^n{P}^{j-1}(f_{\text{I}}+H_{\text{I},1}{u}_1+H_{\text{I},2}{u}_2-G_{\text{I},2}{t}_2)$$

(20)

Then, Eq. (15) can be transformed into

$$\left|\begin{array}{ccccc}{\mathit{H}}_{\mathbf{1},\mathbf{1}}^{\mathbf{1}}+\sum _{\mathit{j}\mathbf{=}\mathbf{1}}^{\mathit{n}}{\left({\mathit{P}}_{\mathbf{1},\mathbf{I}}^{\mathbf{1}}\right)}^{\mathit{j}-\mathbf{1}}{\mathit{H}}_{\mathbf{I},\mathbf{1}}^{\mathbf{1}}& {\mathit{H}}_{\mathbf{1},\mathbf{2}}^{\mathbf{1}}+\sum _{\mathit{j}=\mathbf{1}}^{\mathit{n}}{\left({\mathit{P}}_{\mathbf{1},\mathbf{I}}^{\mathbf{1}}\right)}^{\mathit{j}-\mathbf{1}}{\mathit{H}}_{\mathbf{I},\mathbf{2}}^{\mathbf{1}}& -{\mathit{G}}_{\mathbf{1},\mathbf{2}}^{\mathbf{1}}-\sum _{\mathit{j}=\mathbf{1}}^{\mathit{n}}{\left({\mathit{P}}_{\mathbf{1},\mathbf{I}}^{\mathbf{1}}\right)}^{\mathit{j}-\mathbf{1}}{\mathit{G}}_{\mathbf{I},\mathbf{2}}^{\mathbf{1}}& \mathbf{0}& \mathbf{0}\\ {\mathit{H}}_{\mathbf{2},\mathbf{1}}^{\mathbf{1}}+\sum _{\mathit{j}=\mathbf{1}}^{\mathit{n}}{\left({\mathit{P}}_{\mathbf{2},\mathbf{I}}^{\mathbf{1}}\right)}^{\mathit{j}-\mathbf{1}}{\mathit{H}}_{\mathbf{I},\mathbf{1}}^{\mathbf{1}}& {\mathit{H}}_{\mathbf{2},\mathbf{2}}^{\mathbf{1}}+\sum _{\mathit{j}=\mathbf{1}}^{\mathit{n}}{\left({\mathit{P}}_{\mathbf{2},\mathbf{I}}^{\mathbf{1}}\right)}^{\mathit{j}-\mathbf{1}}{\mathit{H}}_{\mathbf{I},\mathbf{2}}^{\mathbf{1}}& -{\mathit{G}}_{\mathbf{2},\mathbf{2}}^{\mathbf{1}}+\sum _{\mathit{j}=\mathbf{1}}^{\mathit{n}}{\left({\mathit{P}}_{\mathbf{2},\mathbf{I}}^{\mathbf{1}}\right)}^{\mathit{j}-\mathbf{1}}{\mathit{G}}_{\mathbf{I},\mathbf{2}}^{\mathbf{1}}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\mathit{H}}_{\mathbf{2},\mathbf{2}}^{\mathbf{2}}& -{\mathit{G}}_{\mathbf{2},\mathbf{2}}^{\mathbf{2}}& {\mathit{H}}_{\mathbf{2},\mathbf{3}}^{\mathbf{2}}& -{\mathit{G}}_{\mathbf{2},\mathbf{3}}^{\mathbf{2}}\\ \mathbf{0}& {\mathit{H}}_{\mathbf{3},\mathbf{2}}^{\mathbf{2}}& -{\mathit{G}}_{\mathbf{3},\mathbf{2}}^{\mathbf{2}}& {\mathit{H}}_{\mathbf{3},\mathbf{3}}^{\mathbf{2}}& -{\mathit{G}}_{\mathbf{3},\mathbf{3}}^{\mathbf{2}}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& {\mathit{H}}_{\mathbf{3},\mathbf{3}}^{\mathbf{3}}& -{\mathit{G}}_{\mathbf{3},\mathbf{3}}^{\mathbf{3}}\\ \end{array}\right|\left|\begin{array}{c}{\mathit{u}}_{\mathbf{1}}\\ {\mathit{u}}_{\mathbf{2}}\\ {\mathit{t}}_{\mathbf{2}}\\ {\mathit{u}}_{\mathbf{3}}\\ {\mathit{t}}_{\mathbf{3}}\\ \end{array}\right|=\left|\begin{array}{c}{\mathit{f}}_{\mathbf{1}}-\sum _{\mathit{j}=\mathbf{1}}^{\mathit{n}}{\left({\mathit{P}}_{\mathbf{1},\mathbf{I}}^{\mathbf{1}}\right)}^{\mathit{j}-\mathbf{1}}{\mathit{f}}_{\mathbf{I}}\\ {\mathit{f}}_{\mathbf{2}}-\sum _{\mathit{j}=\mathbf{1}}^{\mathit{n}}{\left({\mathit{P}}_{\mathbf{2},\mathbf{I}}^{\mathbf{1}}\right)}^{\mathit{j}-\mathbf{1}}{\mathit{f}}_{\mathbf{I}}\\ \mathbf{0}\\ \mathbf{0}\\ \mathbf{0}\\ \end{array}\right|.$$

(21)

Using Eq. (21), the boundary–volume integral equation numerical method reduces to a relatively inexpensive boundary integral equation method. If the number of unknowns at boundary points is N _l and that of unknowns at internal points is N _p , the matrix Eq. (15) will be reduced from the order (N _l  + N _p ) × (N _l  + N _p ) to N _l  × N _l , which is expected with a great saving of computing time and memory by several orders.

4 Numerical tests

The Born-series method is tested to show its applicability by modeling a semicircular heterogeneous valley and a multilayered heterogeneous model, compared with the full-waveform numerical solution (Fu 2002). Numerical modeling is implemented in the frequency domain. Particular attention is paid to the computational aspect of the method. A variable-element-dimension technique is adopted in the program implementation (Fu 1996) to improve computing speed, in which sampling at three elements per wavelength is sufficient to ensure the accuracy of the results (Campillo 1987). Since the wavelength is a function of frequencies and velocities, the dimension of boundary elements for each subregion in a model is computed according to medium velocity and computational frequency. The model is then discretized in terms of updated element dimensions for individual computational frequencies, respectively. During the numerical implementation, an absorbing boundary element technique (Fu and Wu 2000) is introduced to truncated edges of interfaces to handle artificial reflections arising at the edges of the domain of computation.

The semicircular heterogeneous valley of radius a in an elastic homogeneous half-space is shown in Fig. 2. The dimensionless frequency is defined as η = 2a/λ = aω/πβ, where ω is the circular frequency and β is the velocity of shear wave propagation. The shear wave velocity inside the valley is 1,500 m/s in the background medium of 3,150 m/s. The valley velocity is perturbed randomly by 10 %, 15 %, and 20 %, respectively. The dimensionless frequency responses are computed by the full-waveform numerical solution along the valley surface resulting from a vertical incident SH wave for the dimensionless frequency η = 1.0 (Fig. 3). For the velocity perturbation of 10 % (dash line), we see small amplitude fluctuations along the reference response curve, mainly occurring in the middle of the valley. Remarkable amplitude fluctuations can be expected when the velocity perturbation increases to 15 (hexagram line) and 20 % (dotted line). To make the comparison clearer, the rms error E defined as $E=\sqrt{\sum _{j=1}^N{(x_j^{\prime }-x_j)}^2/\phantom{\sum _{j=1}^N{(x_j^{\prime }-x_j)}^{2}N}N}$ is calculated for all the examples, where x′ presents the approximate solution, x presents the full-waveform solution, and N is the total node number.

Fig. 2

Geometry of a semicircular valley with the radius a, the reference density ${\overline{\mathit{\rho }}}_0$, the reference shear wave velocity ${\overline{\mathit{\beta }}}_0$, and the velocity perturbation δ in the surrounding homogeneous half-space with the density ρ and the shear wave velocity β

Fig. 3

Frequency responses resulting from vertical incident SH wave with η = 1.0 to a semicircular heterogeneous valley for random velocity perturbations of 0 (solid line), 10 % (dash line), 15 % (hexagram line), and 20 % (dotted line)

Figure 4 shows a comparison between the full-waveform solution (solid line) and the Born-approximation solutions of different orders (dash lines) for a velocity perturbation of 10 %. We see that the first-order Born approximation (Fig. 4a) presents a small error around the two sharp edges of the valley by comparing with the full-waveform solution. Figure 4b demonstrates a good agreement between the second-order Born approximation and the full-waveform solution. Figure 5 shows the Born-approximation solutions of different orders (dash lines) at δ = 15 %. We see that the first-order Born approximation (Fig. 5a) significantly underestimates amplitude responses in the middle of the valley, whereas the second-order Born approximation (Fig. 5b) becomes better with small discrepancies observed along the surface of the valley. The fourth-order approximation (Fig. 5d) has an excellent agreement with the full-waveform solution.

Fig. 4

Comparisons between the full-waveform solution (solid lines) and the first-order (a) and second-order (b) Born-approximation solutions (dash lines) for a random velocity perturbation of 10 %. Frequency responses are computed resulting from vertical incident SH wave with η = 1.0 to the semicircular heterogeneous valley. Each rms error E is calculated and shown in the figure

Fig. 5

Comparisons between the full-waveform solution (solid lines) and the first-order (a), second-order (b), third-order (c), and fourth-order (d) Born-approximation solutions (dash lines) for a random velocity perturbation of 15 %. Frequency responses are computed resulting from vertical incident SH wave with η = 1.0 to the semicircular heterogeneous valley. Each rms error E is calculated and shown in the figure

Higher-order Born approximation is required to account for strong volume scattering when the velocity perturbation increases to 20 %, as shown in Fig. 6 for the comparison between the full-waveform solution (solid line) and the approximation solutions of different orders (dash lines). We see that the first-order approximation (Fig. 6a) gives a significant amplitude fluctuation because of huge approximate errors, whereas the third-order approximation (Fig. 6b) largely overestimates amplitude responses, especially for |x| < a. The fifth-order approximation (Fig. 6c) gives a better result, but with some departures mainly around the two sharp edges of the valley. The optimal approximation solution at δ = 20 % is given by the seventh-order approximation (Fig. 6d) with a remarkable agreement between the solid and dash lines.

Fig. 6

Comparisons between the full-waveform solution (solid lines) and the first-order (a), third-order (b), fifth-order (c), and seventh-order (d) Born-approximation solutions (dash lines) for a random velocity perturbation of 20 %. Frequency responses are computed resulting from vertical incident SH wave with η = 1.0 to the semicircular heterogeneous valley. Each rms error E is calculated and shown in the figure

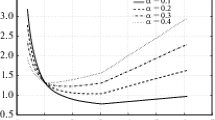
The above comparisons demonstrate that the approximation accuracy of the method decreases gradually with increasing velocity perturbations. The first-order and second-order Born-approximation solutions are valid for velocity perturbations less than 10 % and 15 %, respectively. Figure 7 shows the convergent rate of the method for the semicircular heterogeneous valley with different velocity perturbations. We see that the convergence rate decreases gradually with increasing velocity perturbations. A fast convergence can be achieved for the velocity perturbation less than 15 %. However, the method converges slowly when the velocity perturbation increases to 20 %, and it can hardly converge for the velocity perturbation up to 25 %.

Fig. 7

Convergence of the Born-series approximation method for the semicircular valley with different velocity perturbations of 5 %, 10 %, 15 %, 20 %, and 25 %

To show the applicability of the approximation method, numerical modeling is extended to a heterogeneous multilayered model with randomly velocity perturbations in the surface layer shown in Fig. 8. The other layers are still homogeneous with the velocities indicated in the figure. All the computations of synthetic seismograms are performed with a frequency range of 0–40 Hz, receivers along the free surface, and the source at depth 20 m below the free surface. The source is a minimum-phase Gaussian wavelet with a central frequency of 15 Hz. The dimension of the model is 2,000 m horizontally and 1,000 m vertically. The synthetic seismograms by the full-waveform numerical method (Fu 2002), as shown in Fig. 9, are used as the exact solution for comparisons with the approximation method. We perturb the medium velocity of the surface layer randomly by 5 % and 10 % over the reference velocity 2.5 km/s using white randomness, with the resulting synthetic seismograms displayed in Figs. 9a and b, respectively. We see extremely complex seismic responses with low signal-to-noise ratio because of the diffusion scatterings by the volume heterogeneities in the surface layer. Particularly, the scattered noises become strong for the case δ = 10.

Fig. 8

A heterogeneous multilayered model with random velocity perturbations (δ) in the surface layer

Fig. 9

Synthetic seismograms by the full-waveform numerical method for a multilayered model with random velocity perturbations of 5 % (a) and 10 % (b) in the surface layer

Figure 10 shows the performance of the first-order Born approximation for random velocity perturbations of 5 % and 10 % in the surface layer, respectively. We see that the results have an excellent agreement with the full-waveform solutions shown in Fig. 9. To make the comparison clear, we select several waveform traces with the approximate solutions of different orders for a waveform comparison with the full-waveform solution. As shown in Figs. 11 and 12, the accuracy of the approximation solutions decreases gradually with increasing velocity perturbations. The first-order approximation solution is valid for the velocity perturbation less than 10 %, whereas the second-order approximation gives a more accurate evaluation than the first-order. All of the above simulations of Figs. 9 and 10 are computed on an Intel Core2 P8600 (2.4 GHz) with the Windows XP operating system. The CPU time of the approximation method at the highest computational frequency is 13.1 s, much less than 90.6 s used by the full-waveform numerical method.

Fig. 10

Synthetic seismograms by the first-order approximation of the Born-series method for the multilayered model with random velocity perturbations of 5 % (a) and 10 % (b) in the surface layer

Fig. 11

Comparisons between the full-waveform solution (solid lines) and the first-order (upper panel) and second-order (lower panel) approximation solutions (dotted lines) of the Born-series method for the 35th (a), 40th (b), and 45th (c) traces selected from Fig. 10a associated with a random velocity perturbation of 5 percent in the surface layer of the multilayered model. Each rms error E is calculated and shown in the figure

Fig. 12

Comparisons between the full-waveform solution (solid lines) and the first-order (upper panel) and second-order (lower panel) approximation solutions (dotted lines) of the Born-series method for the 35th (a), 40th (b), and 45th (c) traces selected from Fig. 10b associated with a random velocity perturbation of 10 percent in the surface layer of the multilayered model. Each rms error E is calculated and shown in the figure

5 Conclusions

A flexible approximate solution to the generalized Lippmann–Schwinger integral equation is investigated for wave-propagation simulation in piecewise heterogeneous media, with a great saving of computing time and memory. The Born-series approximation is applied to the volume-scattering wave, with the boundary-scattering wave handled in a fully implicit way. The numerical scheme is validated by dimensionless frequency responses to a heterogeneous semicircular alluvial valley, compared with the full-waveform numerical solution. The approximation method is then applied to a heterogeneous multilayered model for synthetic seismograms to evaluate approximation accuracy.

Numerical experiments indicate that the convergence rate of the method decreases gradually with increasing velocity perturbations. The approximation method has a fast convergence for velocity perturbations less than 15 %. However, the convergence becomes slow drastically when the velocity perturbation increases to 20 %. The method can hardly converge for the velocity perturbation up to 25 %.