Skip to main content
SpringerLink
Log in

Window memoization: an efficient hardware architecture for high-performance image processing

  • Original Research Paper
  • Published:
Journal of Real-Time Image Processing Aims and scope Submit manuscript

Abstract

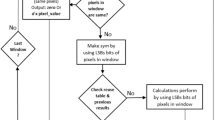
This work presents a new performance improvement technique, window memoization, for hardware implementations of local image processing algorithms. Window memoization combines the memoization techniques proposed in software and hardware with data redundancy in image processing to improve the efficiency of local image processing algorithms implemented in hardware. It minimizes the number of redundant computations performed on an image by identifying similar neighborhoods of pixels in the image and skipping the redundant computations. We have developed an optimized architecture in hardware that embodies the window memoization technique. Our hardware design for window memoization achieves high speedups with an overhead in hardware area that is significantly less than that of the conventional performance improvement techniques. As case studies in hardware, we have applied window memoization to the Kirsch edge detector and median filter. The typical speedup factor in hardware is 1.58 with 40% less hardware in comparison to conventional optimization techniques.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Notes

  1. MSB(d,pix) represents the d most significant bits of pixel pix in window win.

  2. The error in an image (Img) with respect to a reference image (R Img ) is usually measured by signal-to-noise ratio (SNR) as \(SNR = 20log_{10}({\frac{A_{signal}} {A_{noise}}})\) where A is the RMS (root mean squared) amplitude. A 2 noise is defined as: \(A^2_{noise} ={\frac{1} {rc}}\sum_{i=0}^{r-1}\sum_{j=0}^{c-1}(Img(i,j)-R_{Img}(i,j))^2\) where r × c is the size of Img and R Img .

  3. It is worth mentioning that one can calculate the actual time consumed by the base and optimized design to process an input image of n windows of pixels as follows. On average, each window will take \({\frac{1} {thru}}\) cycles to process. If the clock speed is f Hz, then it will take \({\frac{n} {thru \times f}}\) second to process n windows of pixels. In our case studies, the clock speed is 235 MHz. As an example, a 512 × 512 natural image has 510 × 510 windows of 3 × 3 pixels (i.e., n = 510 × 510). For the base design where the throughput is 1, the time will be \({\frac{510 \times 510} {1 \times 235 \times 10^6}}=1.107\,{\rm ms}.\) For natural images, on average, the optimized design throughput is 1.58 times that of the base design. Therefore, the time for the optimized design will be \({\frac{510 \times 510} {1.58 \times 235 \times 10^6}}=0.700\,{\rm ms}.\)

References

  1. Altera Cyclone II FPGAs. http://www.altera.com/products/devices/cyclone2/cy2-index.jsp

  2. Alvarez, C., Corbal, J., Valero, M.: Fuzzy memoization for floating-point multimedia applications. IEEE Trans. Comput. 54(7), 922–927 (2005)

    Article  Google Scholar 

  3. Bloom, B.H.: Space/time trade-offs in hash coding with allowable errors. Commun. ACM 13(7), 422–426 (1970)

    Article  MATH  Google Scholar 

  4. Broder, A., Mitzenmacher, M.: Network applications of bloom filters: a survey. In: Internet Mathematics, pp. 636–646 (2002)

  5. Chen, Y., Kumar, A., Jun (Jim), X.: New design of bloom filter for packet inspection speedup. In: IEEE Global Telecommunications Conference, pp. 1–5 (2007)

  6. Citron, D., Feitelson, D., Rudolph, L.: Accelerating multi-media processing by implementing memoing in multiplication and division units. In: International Conference on Architectural Support for Programming Languages and Operating Systems (ASPLOS-VIII), pp. 252–261 (1998)

  7. Citron, D., Feitelson, D.G.: Hardware memoization of mathematical and trigonometric functions. Technical report, Hebrew University of Jerusalem (2000)

  8. Citron, D., Feitelson, D.G.: “look it up” or “do the math”: an energy, area, and timing analysis of instruction reuse and memoization. In: Power-Aware Computer Systems: Third International Workshop. LNCS, vol. 3164, pp. 101–116. Springer, Berlin (2004)

  9. DeHon, A.: Reconfigurable architectures for general-purpose computing. Technical report, Artificial Intelligence Laboratory, Massachusetts Institute of Technology (1996)

  10. Huang, J., Lilja, D.J.: Extending value reuse to basic blocks with compiler support. IEEE Trans. Comput. 49, 331–347 (2000)

    Article  Google Scholar 

  11. Jain, A.K.: Image data compression: a review. In: Proceedings of the IEEE, vol. 69, pp. 349–389 (1981)

  12. Kavi, K., Chen, P.: Dynamic function result reuse. In: International Conference on Advanced Computing and Communication (ADCOM-03) (2003)

  13. Khalvati, F., Aagaard, M.D., Tizhoosh, H.R.: Accelerating image processing algorithms based on the reuse of spatial patterns. In: Canadian Conference on Electrical and Computer Engineering (CCECE 2007), pp. 172–175 (2007)

  14. Khalvati, F., Tizhoosh, H.R., Aagaard, M.D.: Opposition-based window memoization for morphological algorithms. In: IEEE Symposium on Computational Intelligence in Signal and Image Processing (CIISP 2007), pp. 425–430 (2007)

  15. Kirsch, R.A.: Computer determination of the constituent structure of biological images. Comput. Biomed. Res. 4, 315–328 (1971)

    Article  Google Scholar 

  16. Lipasti, M.H., Wilkerson, C.B., Shen, J.P.: Value locality and load value prediction. In: International Conference on Architectural Support for Programming Languages and Operating Systems (ASPLOS-VII), pp. 138–147 (1996)

  17. Michie, D.: Memo functions and machine learning. Nature 218, 19–22 (1968)

    Article  Google Scholar 

  18. Philips Breast Images. http://www.medical.philips.com /main/products/ultrasoun. Last checked: 20 Jan 2009

  19. Richardson, S.E.: Exploiting trivial and redundant computation. In: IEEE Symposium on Computer Arithmetics, pp. 220–227 (1993)

  20. Robarts Imaging Research Laboratories. http://www.imaging.robarts.c. Last checked: 20 Jan 2009

  21. Semacode Corporation. http://www.semacode.co. Last checked: 20 Jan 2009

  22. Sezgin, M., Sankur, B.: Survey over image thresholding techniques and quantitative performance evaluation. J. Electron. Imaging 13(1), 146 (2004)

    Article  Google Scholar 

  23. Shen, J.P., Lipasti, M.H.: Modern Processor Design. McGraw-Hill, New York (2004)

  24. Sodani, A., Sohi, G.S.: Dynamic instruction reuse. In: International Symposium on Computer Architecture (ISCA-97), pp. 194–205 (1997)

  25. Sonka, M., Hlavac, V., Boyle, R.: Image processing, analysis, and machine vision. PWS (1999)

Download references

Acknowledgments

RADARSAT (i.e., remote sensing) images are copyright of the Canadian Space Agency. We thank the Canadian Ice Service and Prof. David A. Clausi (University of Waterloo) for provision of the image data.

Author information

Authors and Affiliations

  1. Department of Electrical and Computer Engineering, University of Waterloo, Waterloo, ON, Canada

    Farzad Khalvati & Mark D. Aagaard

Authors
  1. Farzad Khalvati
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mark D. Aagaard
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Farzad Khalvati.

Appendix A

Appendix A

1.1 The probability of false positives for parallel reuse tables

Similar to regular parallel Bloom filters, the parallel reuse tables may cause false positives because certain locations in the level 1 reuse tables, which belong to an incoming window may have been filled by different windows. Let the length and width of each reuse table be RT length and RT width , respectively. For windows of m × m pixels, there will be m 2 − 1 reuse tables. Assuming that the hash_keys are random numbers uniformly distributed over the range {1,2, …, RT length }, the probability that a certain location in reuse table RT i has not been inserted with any value is \(1-{\frac{1}{RT_{length}}}.\) Each reuse table entry is RT width bits wide. Thus, each entry can have \(2^{RT_{width}}\) possible values. The probability that a certain location in reuse table RT i has not been inserted with a certain value is \(1-{\frac{1} {RT_{length} \times 2^{RT_{width}}}}.\) After inserting n windows, the probability that a certain location in reuse table RT i has not been inserted with a certain value is \((1-{\frac{1} {RT_{length} \times 2^{RT_{width}}}})^n.\) Thus, the probability that a certain location in reuse table RT i has been inserted with a certain value is \(1-(1-{\frac{1} {RT_{length} \times 2^{RT_{width}}}})^n.\) The probability that certain locations in all m 2 − 1 reuse tables have been inserted with a certain value will be \((1-(1-{\frac{1} {RT_{length} \times 2^{RT_{width}}}})^n)^{m^2-1}.\)

Given that all hash_keys are assumed to be random numbers, the probability that certain locations in all m 2 − 1 reuse tables have been inserted with a certain value indicates the probability of a false positive because random numbers cannot all point to locations that represent a certain value. Thus, the probability of a false positive FP will be:

$$ FP = \left(1-\left(1-{\frac{1} {RT_{length} \times 2^{RT_{width}}}}\right)^n\right)^{m^2-1} $$
(28)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Khalvati, F., Aagaard, M.D. Window memoization: an efficient hardware architecture for high-performance image processing. J Real-Time Image Proc 5, 195–212 (2010). https://doi.org/10.1007/s11554-009-0128-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11554-009-0128-y

Keywords

Search

Navigation