Skip to main content
SpringerLink
Log in

Design of a noise-dependent shrinkage function in wavelet shrinkage of X-ray CT image

  • Original Article
  • Published:
International Journal of Computer Assisted Radiology and Surgery Aims and scope Submit manuscript

Abstract

Purpose

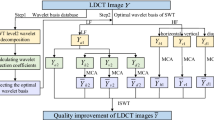
Many shrinkage functions have been introduced and applied for the wavelet shrinkage denoising of computed tomography (CT) images. However, these functions have problems in continuity of functions and cause “shrinkage artifacts”. Therefore, we designed a new and smooth shrinkage function using noise distribution.

Methods

The proposed shrinkage function was designed under the following four conditions: (1) use of noise distribution, (2) shrunk coefficients having all ranges of amplitude, (3) function continuity, and (4) property of a function that is controllable by two parameters. The designed function was applied to phantom and chest CT images and denoising performance was compared with other functions.

Results

In the proposed method, edge and pixel values were maintained when compared with previous functions, the occurrence of shrinkage artifacts was smaller, and high- quality denoised images were obtained.

Conclusions

The proposed shrinkage function is effective for low-dose noisy CT images when using accurately selected parameters.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Endo M, Tsunoo T, Kandatsu S, Tanada S, Aradate H, Saito Y (2003) Four-dimensional computed tomography (4D-CT) concepts and preliminary development. Radiat Med 21: 17–22

    PubMed  Google Scholar 

  2. Abidi MA, Davis PB (1990) Radial noise filtering in positron emission tomography. Opt Eng 29: 567–574. doi:10.1117/12.55625

    Article  Google Scholar 

  3. Chang SG, Yu B, Vetterli M (2000) Adaptive wavelet thresholding for image denoising and compression. IEEE Trans Image Process 9: 1532–1546. doi:10.1109/83.862633

    Article  PubMed  CAS  Google Scholar 

  4. Starck J-L, Candes EJ, Donoho DL (2002) The curvelet transform for image denoising. IEEE Trans Image Process 11: 670–684. doi:10.1109/TIP.2002.1014998

    Article  PubMed  Google Scholar 

  5. Sasaki T, Hanari T, Sasaki M, Oikawa H, Gakumazawa H, Okumura M, Ikeda Y, Toyoshima N (2004) Reduction of radiation exposure in CT perfusion study using a quantum de-noising filter. Jpn J Radiol Technol 60: 1688–1693

    Google Scholar 

  6. Yasuda N, Ishikawa Y, Kodera Y (2005) Improvement of image quality in chest MDCT using nonlinear wavelet shrinkage with trimmed-thresholding. Jpn J Radiol Technol 61: 1599–1608

    Google Scholar 

  7. Yasuda N, Abe S, Nishimura K, Sato H, Yokoyama K, Tomida T et al (2004) Noise reduction in heavy ion CT using wavelet shrinkage. Jpn J Med Phys Suppl 24: 43–44

    Google Scholar 

  8. Yasuda N, Abe S, Nishimura K, Sato H, Tomida T, Muraishi H et al (2003) Comparison of wavelet shrinkage and Fourier noise reductions in heavy ion computed tomography. In: Proceedings of the World Congress on Medical Physics and Biomedical Engineering [CD-ROM] ISBN 1877040142

  9. Nakamori N, Yang Y-Q, Tsunoo T (2003) Effectiveness of wavelet analysis to reduce the patient’s dose for CT images. Jpn J Med Phys Suppl 23: 248–251

    Google Scholar 

  10. Kubota H, Yamazaki Y, Shinohara M, Kawakami K, Murase K (2002) Wavelet de-noising for digital chest radiographs: thresholding by generalized cross validation. Jpn J Med Phys Suppl 22: 188–191

    Google Scholar 

  11. Cherkassky V, Kilts S (2001) Myopotential denoising of ECG signals using wavelet thresholding methods. Neural Netw 14: 1129–1137. doi:10.1016/S0893-6080(01)00041-7

    Article  PubMed  CAS  Google Scholar 

  12. Tikkanen PE (1999) Nonlinear wavelet and wavelet packet denoising of electrocardiogram signal. Biol Cybern 80: 259–267. doi:10.1007/s004220050523

    Article  PubMed  CAS  Google Scholar 

  13. Harpen MD (1999) A computer simulation of wavelet noise reduction in computed tomography. Med Phys 26: 1600–1606. doi:10.1118/1.598654

    Article  PubMed  CAS  Google Scholar 

  14. Yasuda N (2006) Image processing of medical X-ray CT image for improvement of image quality. Doctoral Dissertation, Nagoya University

  15. Sivakumar R (2007) Denoising of computer tomography images using curvelet transform. J Eng Appl Sci 2: 21–26

    Google Scholar 

  16. Donoho DL, Johnstone IM (1995) Adapting to unknown smoothness via wavelet shrinkage. J Am Stat Assoc 90: 1200–1224. doi:10.2307/2291512

    Article  Google Scholar 

  17. Donoho DL (1995) De-noising by soft-thresholding. IEEE Trans Inf Theory 41: 613–27. doi:10.1109/18.382009

    Article  Google Scholar 

  18. Donoho DL, Johnstone IM (1994) Ideal spatial adaption by wavelet shrinkage. Biometrika 81: 425–455. doi:10.1093/biomet/81.3.425

    Article  Google Scholar 

  19. Nason GP (1996) Wavelet shrinkage using cross-validation. J R Stat Soc B 58: 463–479

    Google Scholar 

  20. Yasuda N, Ishikawa Y, Kodera Y (2007) Improvement of edge response in multi-detector row CT by high-spatial-frequency sampling of projection data. Int J CARS 1: 311–320. doi:10.1007/s11548-007-0067-7

    Article  Google Scholar 

  21. Donoho DL (1993) Nonlinear wavelet methods for recovery of signals, densities, and spectra from indirect and noisy data. Proc Symp Appl Math 47: 173–205

    Google Scholar 

  22. Fang H, Huang D (2004) Lidar signal de-noising based on wavelet trimmed thresholding technique. Chin Opt Lett 2: 1–3

    Google Scholar 

  23. Reiter E (1996) Wavelet compression of medical imagery. Telemed J 2: 131–137

    PubMed  CAS  Google Scholar 

  24. Qian J Denoising by wavelet transform. http://www.ruf.rice.edu/%7Ejoejqian/

  25. Jansen M, Malfait M, Bultheel A (1997) Generalized cross-validation for wavelet thresholding. Signal Process 56: 33–44

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Health Sciences, Gifu University of Medical Science, 795-1 Nagamine, Ichihiraga, Seki-shi, Gifu, 501-3892, Japan

    Naruomi Yasuda

  2. School of Health Sciences, Nagoya University, 1-1-20 Daiko-minami, Higashi-ku, Nagoya-shi, Aichi, 461-8673, Japan

    Yoshie Kodera

Authors
  1. Naruomi Yasuda
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yoshie Kodera
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Naruomi Yasuda.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Yasuda, N., Kodera, Y. Design of a noise-dependent shrinkage function in wavelet shrinkage of X-ray CT image. Int J CARS 4, 353–366 (2009). https://doi.org/10.1007/s11548-009-0308-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11548-009-0308-z

Keywords

Search

Navigation