Effect of Movement on the Early Phase of an Epidemic

Abstract

The early phase of an epidemic is characterized by a small number of infected individuals, implying that stochastic effects drive the dynamics of the disease. Mathematically, we define the stochastic phase as the time during which the number of infected individuals remains small and positive. A continuous-time Markov chain model of a simple two-patch epidemic is presented. An algorithm for formalizing what is meant by small is presented, and the effect of movement on the duration of the early stochastic phase of an epidemic is studied.

1 Introduction

Before infectious diseases become full-blown epidemics, they go through an initial phase during which they are subject to sometimes acute stochastic variations. From the perspective of the pathogen, this is a make-or-break phase, where outcomes could go either way: if transmission is to too few individuals, then the disease goes extinct, whereas if enough individuals are infected, an outbreak occurs.

Consider, for instance, the situation shown in Fig. 1, showing SARS-CoV-2 cases in Campbell County (Wyoming) in the early stage of the COVID-19 pandemic. We first observe short outbreaks, isolated in time, with up to 8 cases, then more and more frequent such outbreaks until the start of a major outbreak some time around 20 September 2020, after which case numbers undergo an exponential growth phase for some time (not shown).

Fig. 1

SARS-CoV-2 incidence in Campbell County, Wyoming, from the first case on 2020-03-20, to the start of the exponential increase in case counts (last date shown 2020-10-16)(Color figure online)

The first focus in this work is this pre-exponential phase; in particular, how long does it last and at what prevalence level does the switch occur between such behavior and exponential growth? Note that, as with most recent epidemic outbreaks, the intensity of the effort by public health authorities to limit disease spread must be taken into account: it is likely that the long period before the outbreak seen in Fig. 1 would have been shorter in the absence of public health interventions; see, e.g., Arino et al. (2020).

On the other hand, observe that in Fig. 1, until roughly 6 June, it appears that the disease could die out. It is likely, in this situation, that the observed persistence and transition into an epidemic was the consequence of case importations from nearby jurisdictions. This highlights the second question addressed in this work: does movement between jurisdictions have an effect on the duration of the stochastic phase?

The same type of initial stochastic phase can be observed in many datasets for a variety of different infectious diseases, see, e.g., Andersson et al. (2008), Brandt et al. (1973), Cowling et al. (2008), Hulth et al. (2009), Murphy et al. (1981) and Noyola and Mandeville (2008). One should also bear in mind that there are probably many such phases that do not lead to widespread epidemics and thus are not detected.

Whether these stochastic fluctuations are intrinsic or extrinsic is a hard problem. Altogether, it is indeed likely that the early stochastic phase of an epidemic is driven in part by a succession of “failed” epidemics (from the point of view of the pathogen), in which local extinction would take place were it not for a re-seeding by individuals importing the pathogen from different spatial locations.

There is also a mathematical basis for the distinction of the initial stochastic phase suggested by various approximation techniques developed in the literature. The deterministic and diffusion approximations of Kurtz (1970, 1971) are asymptotic in the population size P, but lose accuracy when the population or the population in any compartment is small; see Ovaskainen and Meerson (2010); Rebuli et al. (2017). This fact is exploited by the hybrid methods of Barbour (1975) and Rebuli et al. (2017). In the former case, branching processes are used in the region of the state space with a small number of infectives, while the CTMC is used in the latter. In both cases, the stochastic models are coupled with deterministic or diffusion approximation once the number of infectives becomes large. LATS (Milliken 2019) is another approximation technique, which constructs a finite state space with a small number of infectives around the disease-free quasi-stationary distribution to study first-passage problems including the probability of a minor epidemic. The algorithm employed below (see Appendix D) to choose the threshold number of infected individuals likewise seeks to minimize the error of calculating the probability of a minor epidemic.

In this paper, we focus on the initial stochastic phase evident from the data and previous mathematical results. We consider a two-patch metapopulation SIS epidemic model coupled by movement between patches, to investigate the effect of varying the overall rate of movement and the distribution of the population among the patches on features of the initial stochastic phase of an epidemic. In Sect. 2, we present the model and modeling assumptions and describe the methods used to formulate the stochastic phase and run the numerous simulations that form the basis of the figures presented throughout. The results of our numerical experiments are presented in Sect. 3. Our results are discussed in Sect. 4. In addition, standard analysis and results along with additional support for the choice of the threshold of infected individuals is presented in the appendices.

2 Model and Methods

In this section, we outline the model, its parameters and underlying assumptions, and the methodologies used to study the effect of movement on the stochastic phase.

2.1 Model

The model comprises two local populations that are coupled together by the movement of individuals. In the absence of movement, each location becomes isolated from the other. In that case, the disease dynamics in each isolated location are described by an SIS epidemic model, which is a variation on a model in Allen and Burgin (2000). A flow diagram of the interactions included in the model is presented in Fig. 2. The model takes the form of a continuous-time Markov chain (CTMC), details of which can be found in Appendix A.

Fig. 2

Flow diagram of the two population SIS epidemic model. The per capita rates of flow between compartments are shown (Color figure online)

The model features patch-specific disease transmission rates $\beta ^X$ and recovery rates $\gamma ^X$, $X = A,\; B$. Movement rates from patch X to patch Y are given by $m^{XY}$ for $X=A,\;B$ and $Y=B,\;A$.

2.2 Methods

2.2.1 Movement Parameters

There are no demographic transitions in the model, so the total population is conserved. We let the total population be given by P. Informed by analysis of a limiting deterministic model (see Appendix B), we note that when we ignore the distinction between susceptible and infected individuals, there is a quasi-stationary distribution for the populations in each patch given by $\left( P^A,\;P^B\right)$, where $P^A$ and $P^B$ depend on the movement rates between patches. To facilitate analysis, we define the parameter $k\in (0,1)$ to be the proportion

$$\begin{aligned} k=\frac{P^A}{P}, \end{aligned}$$

(1)

or, in other words, $P^A=kP$ and $P^B=(1-k)P$. Solving for $m^{BA}$ yields the following expression for $m^{BA}$ in terms of k and $m^{AB}$

$$\begin{aligned} m^{BA}=\frac{k}{1-k}m^{AB}. \end{aligned}$$

(2)

In the numerical experiments presented in Sect. 3, we consider the movement parameters $m^{AB}$ and k to investigate the effect of movement on the duration of the stochastic phase.

2.2.2 Other Parameters

In addition to the movement parameters, other compound parameters and parameter assumptions are important for our investigation. The basic reproduction number is defined as the average number of secondary infections generated, in its infectious lifetime, by a single infected individual in an otherwise totally susceptible population. Despite the fact that this is a statistic that depends on the related mean field system, the basic reproduction number, ${\mathcal {R}}_0$, has been shown to be a threshold value in stochastic systems as well as deterministic ones by Allen and van den Driessche (2013). The basic reproduction number for the two-patch model is given by,

$$\begin{aligned} {\displaystyle \mathcal {R}_0=\frac{\beta ^A\left( \gamma ^B+m^{BA}\right) +\beta ^B\left( \gamma ^A+m^{AB}\right) +\sqrt{\left( \beta ^A\left( \gamma ^B+m^{BA}\right) -\beta ^B\left( \gamma ^A+m^{AB}\right) \right) ^2+4\beta ^A\beta ^B m^{AB}m^{BA}}}{2\left( \left( \gamma ^A+m^{AB}\right) \left( \gamma ^B+m^{BA}\right) -m^{AB}m^{BA}\right) },}\nonumber \\ \end{aligned}$$

(3)

and its derivation is given in Appendix B.

In the absence of movement, we have already noted that the two patches decouple. The basic reproduction in the isolated patch X is given by:

$$\begin{aligned} {\mathcal {R}}_0^X=\frac{\beta ^X}{\gamma ^X}P^X, \end{aligned}$$

(4)

where $\beta ^X$, $\gamma ^X$, and $P^X$ are the transmission rate, recovery rate, and total population in patch $X=A,\; B$, respectively. These patch ${{\mathcal {R}}_0}'s$ are not threshold parameters per se but are used to quantify the overall favorability for disease spread in each location.

We are particularly interested in the case of a medium-sized city and a smaller satellite town or city connected by the movement of individuals. We assume that the communities have relatively similar access to health systems, and we consider the case of a single infectious disease spreading among their residents. As a result, we assume that

$$\begin{aligned} \gamma ^A=\gamma ^B=\frac{1}{7}, \end{aligned}$$

(5)

which corresponds to an average recover time of 1 week. This recovery time is slightly longer than the infectious period for influenza A and slightly shorter than that of mild-to-moderate COVID-19 (Centers for Disease Control and Prevention 2022).

2.2.3 The Stochastic Phase

Stochastic effects dominate population dynamics when populations or subpopulations are small and give way to deterministic population dynamics as populations increase, as implied by the limit theorems of Kurtz (1970, 1971). The hybrid models of Barbour (1975), Rebuli et al. (2017) incorporate a stochastic phase when the population is small in at least one compartment. In the case of epidemic data, time series can be characterized as having a phase of seemingly deterministic growth leading to a major outbreak preceded and followed by periods of stochastic oscillation in the number of cases.

We consider the stochastic phase prior to the deterministic growth that leads to a major outbreak. We are concerned with the case that the number of infected individuals is small. We consider the stochastic phase to be over when either there are no remaining infected individuals, or when the total number of infected individuals $\left( I^A + I^B\right)$ is sufficiently large. The latter case is associated with transition to deterministic growth to an endemic equilibrium of an associated deterministic model. Therefore, sample paths that reach a sufficiently large number ${\hat{I}}$ of total infected individuals are associated with a major outbreak, while sample paths that reach zero total infected individuals before ${\hat{I}}$ are associated with disease extinction.

Accurately characterizing the stochastic phase is therefore equivalent to determining an appropriate choice for the threshold number of total infected individuals ${\hat{I}}$. Since reaching ${\hat{I}}$ total infected individuals is associated with transition to deterministic growth, we assume that once the threshold ${\hat{I}}$ is reached, a major outbreak occurs with probability 1. For an appropriately chosen ${\hat{I}}$, a CTMC with stopping criteria $I^A+I^B=0$ and $I^A+I^B={\hat{I}}$ would approximate the probability of a major outbreak with a high degree of accuracy. Without loss of generality, we instead consider the probability of extinction. The true probability of extinction can be estimated various ways. One method is to choose stopping criteria as described above, but let ${\hat{I}}$ be equal to the sum of infected individuals at the endemic quasi-stationary distribution predicted by the associated deterministic model. Such a model can be simulated repeatedly, and the probability of extinction can be estimated by the proportion of sample paths that terminate in the extinction stopping criterion $I^A+I^B=0$. However, this method comes at a high computational expense. Instead, we approximate the probability of extinction using multitype branching process (MTBP) approximation (see Milliken (2017); Tritch and Allen (2018)). Details of the MTBP approximation can be found in Appendix C. Since the duration of the stochastic phase is partly dependent on the choice of ${\hat{I}}$, we assume

$$\begin{aligned} {\hat{I}}=35, \end{aligned}$$

(6)

for all parameter choices. The fact that ${\hat{I}}=35$ in a population of one million individuals is consistent with the error bound provided by the LATS method of Milliken (2019). Additional supporting evidence and greater detail regarding the choice of ${\hat{I}}$ can be found in Appendix D.

2.2.4 Numerical Simulations

The heatmaps in Sect. 3 are obtained by varying a pair of parameters while leaving the remaining parameters fixed, resulting in over 3000 parameter combinations. For each parameter combination, we simulate an ensemble of 100,000 sample paths. In some cases, sample paths wander into regions of the state space where the inter-event time becomes very small. This can be viewed as similar to stiffness in simulating ordinary differential equations and leads to high computational expense. To avoids these problems, we employ an adaptive tau leap algorithm for approximate stochastic simulation using R package adaptivetau. The algorithm is run in parallel on multicore research computing servers.

3 The Effect of Movement

As noted in Sect. 2.2.1, all movement is controlled by the rate $m^{AB}$ of movement from patch A to patch B, and the long-term average proportion k of the total population present in patch A. Recall, (2) shows that $m^{AB}$ and k uniquely determine $m^{BA}$. The duration of a minor epidemic has been studied by Tritch and Allen (2018). As a control, we first illustrate how the duration of the stochastic phase differs from the duration of a minor epidemic in a single population. We then investigate the effect of changing $m^{AB}$ (respectively k) both alone and varying with other key system parameters.

3.1 Duration of the Stochastic Phase in a Single Population

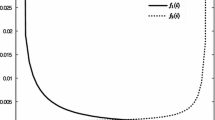
The term minor epidemic appears in Whittle (1955) and is characterized as being generally shorter in duration and having fewer cases than a major one. In the context of what we call the stochastic phase, minor epidemics are sample paths that lead to the extinction stopping criterion without reaching the threshold ${\hat{I}}$. Tritch and Allen (2018) found that the mean duration of a minor epidemic peaks around the threshold criterion ${\mathcal {R}}_0=1$. However, in that paper, Tritch and Allen also note that when ${\mathcal {R}}_0>1$, sample paths that lead to a major outbreak have a longer mean duration, on average. In the stochastic phase, major epidemics are sample paths leading to the threshold $I^A+I^B={\hat{I}}$ before $I^A+I^B=0$. Since the threshold ${\hat{I}}$ is typically chosen to be smaller than the total number of cases at the endemic quasi-stationary distribution, the duration of these sample paths in the stochastic phase is typically shorter than their duration in an unabridged model. In Fig. 3, we take patch A to be a single patch isolated from patch B. We see that the mean duration of sample paths that lead to extinction (shown in green) peaks around ${\mathcal {R}}_0^A=1$, while the mean duration of sample paths stopping after reaching ${\hat{I}}$ (shown in red) peaks for ${\mathcal {R}}_0^A>1$. As a consequence, the mean duration of the stochastic phase (which includes all paths and is shown in black) is shifted to the right of ${\mathcal {R}}_0^A=1$. The shaded regions show the range of durations across the $10^5$ simulations run for each value of ${\mathcal {R}}_0^A$. The light shaded region represents the sample paths in the 97.5 percentile and not in the 2.5 percentile. The dark shaded region represents sample paths in the 75 percentile and not in the 25 percentile (the interquartile range).

Fig. 3

Mean duration of the stochastic phase in a single population patch A for various values of ${\mathcal {R}}_0^A$ (Color figure online)

3.2 The Effect of $m^{AB}$

Recall from (2), $m^{BA}$ can be expressed as a function of $m^{AB}$ and k. As a result,

$$\begin{aligned} m^{AB} + m^{BA} = \frac{1}{1-k}m^{AB}, \end{aligned}$$

(7)

that is, we can vary the overall rate of moving between patches by varying $m^{AB}$. Thus, as $m^{AB}$ approaches zero, movement between patches becomes a rare event and as $m^{AB}$ becomes very large, movement becomes so frequent as to minimize local features and make the system resemble a homogeneous single population. Deterministic metapopulation models exhibit similar behavior as movement rates become arbitrarily large. Unlike deterministic models, however, our simulations show that for $m^{AB}$ small, the behavior of the stochastic metapopulation model depends on the patch in which the disease is introduced. That is, stochastic metapopulations coupled by very rare movement between patches behave similarly to a system of isolated populations. Furthermore, as the strength of the coupling as measured by $m^{AB}$ initially increases, the behavior of the model continues to depend on the patch of introduction. From the stand point of probability of extinction and mean duration of an outbreak, the model still behaves a little bit like a decoupled system, except that the features of each patch are perturbed by the influence of the neighboring patch. The behavior of a two-patch system as $m^{AB}$ varies is presented in Fig. 4.

Fig. 4

Range of durations (shaded) and mean duration (line) of the stochastic phase versus $m^{AB}$ with disease introduced in patch A (red) or B (blue) for ${\mathcal {R}}_0^A=1.2$, ${\mathcal {R}}_0^B=2.5$ and $k=0.9$ (Color figure online)

Of course, $m^{AB}$ is not the only parameter that effects the mean duration of the stochastic phase. A benefit of the simplicity of our model is that it is easier to investigate the correlation between the relatively few model parameters. The only model parameters besides $m^{AB}$ and k are the patch dependent infection rates $\beta ^A,\;\beta ^B$ and the recovery rate $\gamma := \gamma ^A=\gamma ^B$. For each fixed k, (1) implies that $P^A$ and $P^B$ are also fixed. Since $\gamma$ is fixed, ${\mathcal {R}}_0^X$ varies linearly with $\beta ^X$, $X=A,\;B$. However, since ${\mathcal {R}}_0^X$ has a more natural interpretation, we represent varying $m^{AB}$ with $\beta ^X$ as varying $m^{AB}$ with ${\mathcal {R}}_0^X$.

Fig. 5

Mean duration (in days) of the stochastic phase for varying values of $m^{AB}$ and ${\mathcal {R}}_0^A$ with ${\mathcal {R}}_0^B=2.5$ where $k=0.1$ on the left and $k=0.9$ on the right. Blue: value of the reproduction number for the two-patch model as given by (3) (Color figure online)

Fig. 6

Left: Mean duration (in days) of the stochastic phase for varying values of $m^{AB}$ and ${\mathcal {R}}_0^B$ with $k=0.9$ and ${\mathcal {R}}_0^A=2.5$. Right: Mean duration of the stochastic phase for varying values of $m^{AB}$ and ${\mathcal {R}}_0^B$ with $k=0.9$ and ${\mathcal {R}}_0^A=1.2$ (Color figure online)

Figure 5 consists of heat maps of the mean duration of the stochastic phase varying $m^{AB}$ and ${\mathcal {R}}_0^A$ while keeping ${\mathcal {R}}_0^B=2.5$. The graph on the left shows the results for $k=0.1$ and the one on the right represents the case $k=0.9$. The red lines are level curves for the mean duration of the stochastic phase, and the blue lines are level curves for ${\mathcal {R}}_0$. When $k=0.1$, then $m^{BA}=\frac{1}{9}m^{AB}$. In that case, for each choice of ${\mathcal {R}}_0^A$, the mean duration is decreasing in $m^{AB}$. For each $m^{AB}$ there is a value of ${\mathcal {R}}_0^A>1$ which maximizes the mean duration and that value increases with $m^{AB}$. In the right-hand plot of Fig. 5, $k=0.9$ and $m^{BA}=9\cdot m^{AB}$, almost an order of magnitude larger. For small values of $m^{AB}$, the mean duration is decreasing in $m^{AB}$, at least for ${\mathcal {R}}_0^A<2.5$. This is likely due to the fact that ${\mathcal {R}}_0^B=2.5$ so that, when $m^{AB}$ is relatively small, infected individuals are making extended sojourns into a patch where the path to either extinction or the threshold ${\hat{I}}$ is more direct. However, the mean duration’s dependence on $m^{AB}$ is non-monotone. As $m^{AB}$ increases in this scenario, the outsized increase in $m^{BA}$ means that whenever an infectious individual moves from patch A to patch B it is much more likely to move back quickly. For large $m^{AB}$, movement becomes more frequent and individuals approach the deterministic behavior of spending approximately k proportion of their lifetime in patch A.

Typically two-patch models exhibit symmetry and simplicity that make them less interesting to study. However, the introduction of the parameter k in order to preserve a roughly constant proportion of the population in each patch obscures this symmetry and reveals complex and interesting behavior in even this simple model. Figure 6 shows heat maps of the mean duration while varying $m^{AB}$ and ${\mathcal {R}}_0^B$ when ${\mathcal {R}}_0^A=1.2$ and $k=0.1$ (left) or $k=0.9$ (right). Note that regardless of k, when $m^{AB}$ is small, there is not much dependence on ${\mathcal {R}}_0^B$, since movement is rare and the disease is introduced into patch A. On the left, $k=0.1$ and the dependence of mean duration is on both $m^{AB}$ and ${\mathcal {R}}_0^B$. This is due to the fact that $m^{BA}$ is nearly an order of magnitude smaller than $m^{AB}$. On the right, where $m^{BA}$ is nearly an order of magnitude larger, as $m^{AB}$ increases, the dependence of the mean duration on ${\mathcal {R}}_0^B$ is much stronger.

3.3 The Effect of k

In this section, we investigate the effect of changes to the population proportion parameter k on the mean duration of the stochastic phase. We have already seen some evidence of the effect of k in Figs. 5 and 6. In both those figures, there are two panels with $k=0.1$ on the left and $k=0.9$ on the right. Within each pair, we see that the simulation results are qualitatively similar for small values of $m^{AB}$. Differences between $k=0.1$ and $k=0.9$ begin to emerge as $m^{AB}$ becomes larger. As previously noted, this is not directly the result of the population proportion itself, but rather its indirect role in determining $m^{BA}$.

Fig. 7

Mean duration (days) of the stochastic phase as k varies with ${\mathcal {R}}_0^A$ (left) and ${\mathcal {R}}_0^B$ (right)(Color figure online)

Figure 7 also presents two heat maps of the mean duration of the stochastic phase varying k together ${\mathcal {R}}_0^A$ on the left and ${\mathcal {R}}_0^B$ on the right. For these illustrations, $\gamma = 1/7$, $m^{AB}=0.001$, and the disease is introduced in patch A. When not varying, ${\mathcal {R}}_0^A=1.2$ and ${\mathcal {R}}_0^B=2.5$. Both panels indicate that for $k<0.5$ ($m^{BA}\!\le \! m^{AB}$), the mean duration of the stochastic phase is almost independent of k. As k increases to 1, any movement away from patch A where the disease is introduced is followed with high likelihood by a quick return. That is, the model behaves even more like an uncoupled patch A system. It is evident from the panel on the right that, as k approaches 1, the mean duration of the stochastic phase rapidly shifts from strong dependence on ${\mathcal {R}}_0^B$ to becoming nearly independent of the reproduction number in the neighboring patch.

3.4 Comparing the Effect of $m^{AB}$ and k

To this point, we have investigated the effect of varying $m^{AB}$ and the effect of varying k on the mean duration of the stochastic phase, but we have yet to fully consider the effects of varying both movement parameters simultaneously. Still, the pairs of heat maps in Figs. 5, 6, and 7 do give us the basis to make the hypothesis that the mean duration is strongly dependent on changes to $m^{AB}$ and only begins to depend on k when it is near enough to 1 so that $m^{BA}$ becomes very large. To test this hypothesis, we prepared the heat map presented in Fig. 8. The mean duration is calculated for various values of $m^{AB}$ and k with ${\mathcal {R}}_0^A=1.2$, ${\mathcal {R}}_0^B=2.5$, and $\gamma =\frac{1}{7}$. The figure confirms our hypothesis that the mean duration depends on $m^{AB}$ and only on k near 1 when the value of k guarantees that $m^{BA}$ becomes large relative to $m^{AB}$.

Fig. 8

Mean duration (days) of the stochastic phase as a function of $m^{AB}$ and k (Color figure online)

4 Discussion

Data and mathematical theory agree that systems described by compartmental models exhibit stochastic behavior when the population of at least one compartment is small. However, as the population increases the behavior of such a system, and models trying to represent it, becomes more deterministic. In the case of epidemic models, stochastic effects are always a factor following the emergence or re-emergence of an infectious disease. The transient dynamics following (re)introduction of the disease before either extinction or the onset of deterministically driven dynamics is described as the stochastic phase. A formal method for characterizing the stochastic phase by defining a threshold number of infected individuals is proposed. The threshold number of cases, ${\hat{I}}$, is determined so that the resulting truncated model detects the probability of disease extinction to a desired sensitivity. It is interesting to note that in a system with a total population of one million individuals, ${\hat{I}}=35$ is found to be a sufficient threshold number of cases across a wide range of parameters. Details regarding the choice of ${\hat{I}}$ are presented in Appendix D.

The effect of movement on the mean duration of the stochastic phase is investigated numerically for the case of a relatively simple two-patch SIS epidemic model. The two-patch case was chosen to reflect the setting of a medium-sized city and a smaller satellite city with an infectious disease circulating between the two populations. Despite the simplicity of the model, numerical experiments still yielded complex and interesting results. The choice of only two population patches also served to highlight a key feature of stochastic metapopulation models that differs from deterministic metapopulation models taking the form of a system of nonlinear ordinary differential equations. Namely, dynamics are highly dependent on the patch of disease (re-)emergence.

The sample paths leading to the end of the stochastic phase may terminate in disease extinction or reach the threshold number of cases indicating an outbreak. On average, the duration of sample paths leading to outbreak is longer than those leading to extinction. As the favorability for disease spread, as measured by the reproduction number, increases, paths leading to outbreak become more likely, but all paths become more direct and duration decreases. Even in a single, isolated population, the mean duration of the stochastic phase peaks for ${\mathcal {R}}_0$ to the right of the classic threshold ${\mathcal {R}}_0=1$. This is an important distinction, since the mean duration of paths that lead to extinction (also known as minor epidemics) peaks at ${\mathcal {R}}_0=1$.

The effect of movement is captured in parameters $m^{AB}$ and k. The parameter $m^{AB}$ represents the rate of movement from patch A to B, but also the overall frequency of movement. The parameter k represents the average proportion of the population in patch A, but also defines the rate of movement from patch B to A, for each value of $m^{AB}$. The effect of varying these parameters alone, together and with the patch-specific rate of disease transmission (represented by the patch-specific ${\mathcal {R}}_0$), is studied by numerical experiment. For each parameter combination, $10^5$ simulations are performed and their duration averaged. The massive computational expense is mitigated by taking advantage of advanced stochastic simulation techniques provided by a tau leaping method in R (adaptivetau).

Analysis shows that the mean duration of the stochastic phase generally decreases with the rate of movement $m^{AB}$ when the patch of disease (re-)emergence is coupled to a patch more favorable to the spread of the disease. This relationship is not monotone, however. For example, when k is large (greater than 0.5), increasing $m^{AB}$ indicates an even larger increase in $m^{BA}$ and the system resembles the patch of disease (re-) emergence being coupled to a patch less favorable to the spread of disease. In that case, the mean duration can actually begin to increase with increasing $m^{AB}$. In contrast, the mean duration of the stochastic phase does not seem to depend strongly on the proportionality constant k. However, this conclusion also has its exception when k approaches 1. The exception is driven by k’s role in defining $m^{BA}$. That is, even for fixed $m^{AB}$, $m^{BA}$ increases to infinity as k increases to 1.

Analysis and simulations presented here are not meant to be interpreted as a real-world case study. Rather, they are meant to provide understanding of general changes to the qualitative behavior of the early stochastic phase of an epidemic resulting from changes to control the rate of disease spread locally or to control movement between populations. The stochastic phase is important to understand because it is the phase during which any particular outbreak could go away or lead to an epidemic. While some individual sample paths spent more than a year in the stochastic phase, the mean duration is generally less than a month. This means that public health strategies have to be able to be quickly deployed in order to have an effect on an outbreak during this critical phase. Additionally, the threshold ${\hat{I}}=35$ indicates the need for ongoing development of rapid and reliable surveillance programs to catch an outbreak before it moves into a deterministic growth phase.

Appendices

Appendix A Two-Population Stochastic CTMC Model

We formulate a CTMC model for the two population system as

$$\begin{aligned} {\mathbf {X}}(t)=\left( S^A(t),I^A(t),S^B(t),I^B(t)\right) , \end{aligned}$$

a generalized birth-and-death process which takes the 4-dimensional lattice of non-negative integers as its state space. The Markov chain ${\mathbf {X}}(t)$ is characterized by the transitions

$$\begin{aligned} P\left( {\mathbf {X}}(t+\varDelta t)={\mathbf {j}}|{\mathbf {X}}(t)={\mathbf {i}}\right) =\sigma ({\mathbf {i}},{\mathbf {j}})\varDelta t +o(\varDelta t), \end{aligned}$$

(8)

with rates $\sigma (i,j)$ given in Table 1.

Table 1 Transition rates for the CTMC ${\mathbf {X}}(t)$

Appendix B Limiting Deterministic Model

The two population deterministic SIS model is a two-patch metapopulation model in the form of the following system of ODEs

$$\begin{aligned} \dot{S}^A&= -\beta ^A S^A I^A + \gamma I^A - m^{AB}S^A + m^{BA} S^B,\end{aligned}$$

(9a)

$$\begin{aligned} \dot{I}^A&= \beta ^A S^A I^A - \gamma I^A - m^{AB}I^A + m^{BA}I^B,\end{aligned}$$

(9b)

$$\begin{aligned} \dot{S}^B&= -\beta ^B S^B I^B + \gamma I^B + m^{AB}S^A - m^{BA} S^B,\end{aligned}$$

(9c)

$$\begin{aligned} \dot{I}^B&= \beta ^B S^B I^B - \gamma I^B + m^{AB}I^A - m^{BA}I^B, \end{aligned}$$

(9d)

where $S^\alpha ,I^\alpha$ are the state variables, and $\beta ^\alpha$ and $\gamma ^\alpha$ are the disease characteristic parameters in patch $\alpha =A$ or B. The meaning of $S^\alpha$, $I^\alpha$, $\beta ^\alpha$ and $\gamma ^\alpha$ is patch-specific, but otherwise the same as in the single population case. The two population patches are coupled together by movement with movement rates $m^{AB}$ from patch A to patch B and $m^{BA}$ from B back to A.

Let $P^\alpha (t)=S^\alpha (t)+I^\alpha (t)$ be the total population in patch $\alpha =A$ or B. Then,

$$\begin{aligned} {{\dot{\mathbf {P}}}} = \mathcal {M}\mathbf {P}, \end{aligned}$$

(10)

where $\mathbf {P}(t)=(P^A(t),P^B(t))^T$ and

$$\begin{aligned} \mathcal {M}= \begin{pmatrix} -m^{AB} &{} m^{BA} \\ m^{AB} &{} -m^{BA} \end{pmatrix}. \end{aligned}$$

Let $P^\star =P^A+P^B$. Then, $\dot{P}^\star =0$ and $P^\star$ is a conserved quantity. Solving (10) yields the unique equilibrium

$$\begin{aligned} {\bar{\mathbf {P}}}=\begin{pmatrix}{\bar{P}}^A\\ {\bar{P}}^B\end{pmatrix}=\frac{P^\star }{m^{AB}+m^{BA}}\begin{pmatrix}m^{BA}\\ m^{AB}\end{pmatrix}. \end{aligned}$$

(11)

Thus, (10) is a monotone planar system and (11) is globally asymptotically stable; see Smith (1995). This simple result is important to our study, since it means that we can tune patch populations to be any convex combination with $P^A+P^B=P^\star$. For the purpose of numerical experiments, we set one patch as a medium-size population and the other as a small population, and this relationship remains constant in the case of the deterministic system. The deterministic equilibrium (11) represents a quasi-stationary distribution in the two-patch SIS CTMC model described in Appendix A. Therefore, realizations will preserve the relationship of one medium-sized population and one small-sized population for long time frames, although there will be some fluctuation.

Appendix C Multitype Branching Process Approximation

Let $Z=\left( I^A,I^B\right)$ be the multitype branching process approximation of CTMC ${\mathbf {X}}(t)$ with infected types $I^A$ and $I^B$. Following Allen and Lahodny (2012, 2013), Harris (1963), Milliken (2017), we define the type A and B offspring probability-generating functions

$$\begin{aligned} f_A(u_1,u_2)&=\frac{\gamma ^A+m^{AB}u_2+\beta _Au_1^2}{\gamma ^A+m^{AB}+\beta _A}\end{aligned}$$

(12a)

$$\begin{aligned} f_B(u_1u_2)&=\frac{\gamma ^B+m^{BA}u_2+\beta _Bu_1^2}{\gamma ^B+m^{BA}+\beta _B}. \end{aligned}$$

(12b)

Let $F:[0,1]^2\rightarrow [0,1]^2$ be given by ${\mathbf {F}}(u_1,u_2)=\left( f_A(u_1,u_2),f_B(u_1,u_2)\right)$. By the threshold theorem of Allen and van den Driessche (2013) and the criticality theorem of Harris (1963), if $\mathcal {R}_0>1$, there exists a unique ${\mathbf {q}}=(q_A,q_B)\in [0,1)^2$ such that ${\mathbf {F}}({\mathbf {q}})={\mathbf {q}}$. For $I^A(0)={i_A}_0$ and $I^B(0)={i_B}_0$ sufficiently small, then the probability of extinction from the initial state $({i_A}_0,{i_B}_0)$ is

$$\begin{aligned} \lim _{n\rightarrow \infty } \mathbb {P}(Z(n)=0|Z(0)=({i_A}_0,{i_B}_0))=q_A^{{i_A}_0}q_B^{{i_B}_0}. \end{aligned}$$

(13)

The probability of extinction if there is initially a single infected individual of A (resp. B) is $q_A$ (resp. $q_B$).

Appendix D The Choice of Threshold ${\hat{I}}$

We claim that the model will evolve in a deterministic way after leaving the stochastic phase. In the case of stopping due to reaching ${\hat{I}}$, deterministic behavior after that point means that the time series of the process should go to the endemic quasi-stationary distribution with probability 1. The probability of a minor epidemic is denoted ${\mathbb {P}}_0$ and the probability of a major epidemic $1-{\mathbb {P}}_0$. By the Markov property, when ${\hat{I}}$ is sufficiently large the probability of reaching ${\hat{I}}$ number of infected individuals before reaching zero is ${\mathbb {P}}_0$.

Fig. 9

Absolute value of the difference between the MTBP and stochastic phase approximations of ${\mathbb {P}}_0$ as a function of the threshold ${\hat{I}}$ and $m^{AB}$ (Color figure online)

Fig. 10

Absolute value of the difference between the MTBP and stochastic phase approximations of ${\mathbb {P}}_0$ as a function of the threshold ${\hat{I}}$ and ${\mathcal {R}}_0^A$. In alphabetical order ${\mathcal {R}}_0^B$ = 0.8, 1.2, 2.5 (Color figure online)

For any one choice of parameters, we approximate ${\mathbb {P}}_0$ using a MTBP and then run an ensemble of $10^5$ simulations for the probability absorption in $I_A+I_B=0$. This is then repeated for progressively larger values of ${\hat{I}}$ until the desired precision is reached. Note that the precision is not solely limited by ${\hat{I}}$. Since the probability of extinction in the stochastic phase is approximated as the proportion of paths absorbed in $I_A+I_B=0$, it is roughly accurate to the reciprocal of the square root of the number of simulations in each ensemble.

We are concerned with comparing many parameter combinations. The choice of ${\hat{I}}$ influences the duration of the stochastic phase. To see this, just note that the shortest path to ${\hat{I}}$ gets longer as ${\hat{I}}$ gets larger. In order to compare the mean duration of the stochastic phase across many parameter combinations, we choose a value of ${\hat{I}}$ which is suitable for the range of parameter choices. Figure 9 is a heat map of the absolute value of the difference between the MTBP and stochastic phase approximations of ${\mathbb {P}}_0$ as a function of ${\hat{I}}$ and $m^{AB}$. Figure 10 shows the same heat map as a function of ${\hat{I}}$ and ${\mathcal {R}}_0^A$. The three panels shown in Fig. 10 differ only by the choice of ${\mathcal {R}}_0^B$. Due to the number of simulations per parameter choice, the accuracy is limited to roughly $3\times 10^{-3}$. On the basis of these exhibits, we set ${\hat{I}}=35$ for the numerical experiments presented throughout the body of the article.