Abstract
A functional differential model of SEIS-M type with two time delays, representing the response time for mass media to cover the current infection and for individuals’ behavior changes to media coverage, was proposed to examine the delayed media impact on the transmission dynamics of emergent infectious diseases. The threshold dynamics were established in terms of the basic reproduction number \({\mathcal {R}}_{0}\). When there are no time delays, we showed that if the media impact is low, the endemic equilibrium is globally asymptotically stable for \({\mathcal {R}}_{0}>1\), while the endemic equilibrium may become unstable and Hopf bifurcation occurs for some appropriate conditions by taking the level of media impact as bifurcation parameter. With two time delays, we comprehensively investigated the local and global bifurcation by considering the summation of delays as a bifurcation parameter, and theoretically and numerically examined the onset and termination of Hopf bifurcations from the endemic equilibrium. Main results show that either the media described feedback cycle, from infection to the level of mass media and back to disease incidence, or time delays can induce Hopf bifurcation and result in periodic oscillations. The findings indicate that the delayed media impact leads to a richer dynamics that may significantly affect the disease infections.
Similar content being viewed by others
1 Introduction
Since the 2003 outbreak of severe acute respiratory syndrome (SARS) and the 2009 novel influenza A(H1N1) pandemic, global public health systems of surveillance and response have been substantially improved. In order to quickly curb an emerging disease and reduce its influence on socioeconomic activities, each country developed its effective public health information processing system. With the massive news coverage and fast information flow on the emerging diseases, the public may alter individuals’ behavior and consequently implement some control measures. There are a number of mathematical models describing the media impact on disease transmission (Verelst et al. 2016; Funk 2010; Yan et al. 2018, 2016; Funk et al. 2015; Mao 2014; Cui et al. 2008a, b; Xiao et al. 2013, 2015; Tang et al. 2010; Liu et al. 2007; Li and Cui 2009; Tchuenche et al. 2011; Sun et al. 2011; Wang and Xiao 2014; Song and Xiao 2018). The most general approach is to change the incidence rate by including a function which is decreasing in the number of infected individuals. For example, Liu et al. (2007) introduced a media function \(\beta e^{-\alpha _1 E-\alpha _2 I-\alpha _3 H}\) into the transmission coefficient, where E, I and H are the numbers of reported exposed, infectious and hospitalized individuals, respectively. Li and Cui (2009) used a factor \(\beta _1-\beta _2 \frac{I}{m+I}\) (or \(\beta _2 \frac{I}{m+I}\)) to reflect the reduced amount of contact rate due to media coverage. Xiao et al. (2015) extended these media functions by assuming that the function depends on both the case number and its rate of change, and obtained that media impact switches on and off in a highly nonlinear fashion. Yan et al. (2016) further extended these models by including extra compartment, i.e., the level of media coverage M, and consequently, media impact is modeled by including the function \( e^{-\mu M}\) with \(\mu > 0\) in the incidence.
Basically, these models, described by ordinary differential equations (Liu et al. 2007; Cui et al. 2008b; Li and Cui 2009; Sun et al. 2011; Xiao et al. 2015; Yan et al. 2016), ignored the time duration for individuals’ response to the media coverage and the time duration for the mass media’s response to the disease infection. In fact, by analyzing the number of hospital notifications of the Shaanxi province and the number of daily news items from the eight popular sources during September 3, 2009, to November 16, 2009, Yan et al. (2016) obtained the correlation between the case number and media coverage, confirmed the existence of time lags and further identified the time lags. Hence, it is more reasonable to include time delay in the incidence rate when modeling media impact on transmission dynamics. Recently, we (Song and Xiao 2018) initially included time delay in the media function \( e^{-\alpha I(t-\tau )}\) with positive constant \(\alpha \) and examined the global bifurcation of the proposed system. However, time delays may not be single but multiple. They are associated with the duration of mass media’s response to infection or the duration of individuals’ response to mass media. How these delays mutually affect dynamics of infection and which one is key for the complex dynamics remain unclear. Therefore, these issues are of great importance for future epidemics control, and investigating the impact of delayed mass media on disease spread falls within the scope of this study.
The purpose of this study is to investigate the multiple-delay-mediated media impact on the transmission dynamics of infectious diseases, based on the mathematical model with extra compartment of media coverage. We shall examine the threshold dynamics and global bifurcation of the proposed system in order to know how the refined media function affects the global dynamics of disease transmission and consequently address the effect of media coverage on disease transmission.
2 Model Description
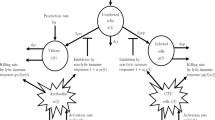
The underlying structure of the model comprises of classes of individuals that are susceptible (S), exposed but not yet infectious (E) and infected (I). The susceptible individuals are infected by infectious individuals with a rate of \(\beta \), and become exposed; exposed individuals become infectious with a rate \(\sigma \); infected individuals are recovered with a rate \(\gamma \) and back into the susceptible class. On the basis of the SEIS-type model, we include the media coverage as an independent variable, denoted by M(t), which is the average number of news items related to the outbreak. The changing rate of the average number of daily news items is assumed to depend on the number of infected individuals at time \(t-\tau _1\) with a rate of \(\delta \), where time delay \(\tau _1\) represents the reported delay and the mass media’s response duration.
Media coverage and fast information flow have significant impact on the avoidance behaviors at both individual and society levels, and the average number of daily news items has clearly profound psychological impact on the social conduct that seems to reduce the effective contact of susceptible with infectious individuals. An exact functional description for media impact is not available and would be extremely difficult to achieve. Here we assume that the media impact depends on the average number of daily news items, and it is described by an exponential decreasing factor (Liu et al. 2007). Hence, a reduction in the incidence rate is represented by \(e^{-\alpha M(t-\tau _2)}\), where time delay \(\tau _2\) denotes the time duration for individuals’ response to the current media coverage. Thus the model equations are
where \(\varLambda \) stands for the rate of flow into the population, d is the natural death rate, \(\beta \) denotes the baseline transmission rate and \(\mu \) represents media spontaneous disappearance rate. All parameters are nonnegative constants.
It is easy to obtain that the total population size \(N(t):=S(t)+E(t)+I(t)\) satisfies \(N'=\varLambda -d N\), which gives \(\lim _{t\rightarrow +\infty }N(t)=\frac{\varLambda }{d}\doteq {\bar{N}}\). Thus system (1) is equivalent to the following system:
and has a limiting system
Let \(X=C([-\tau ,0], R^{4})\) with the supremum norm \(\parallel \parallel _{\infty }\) where \(\tau =\max \{\tau _{1}, \tau _{2}\}\), then X is an ordered Banach space with the cone \(X^{+}\) consisting of all nonnegative functions in X. Let \(Y=C([-\tau ,0],R^{3})\) be the ordered Banach space with the cone \(Y^{+}\) consisting of all nonnegative functions in Y. We also denote
We have the following preliminary results for systems (1, 2, 3):
Theorem 1
-
(i)
For initial value \(\varphi \in X^{+}\), system (1) admits a unique nonnegative bounded solution \(u(t, \varphi )\) on \([0, \infty )\) with \(u_{0}=\varphi \), and \(u_{t}(\varphi ):=(u_{1t}(\varphi )\), \(u_{2t}(\varphi )\), \(u_{3t}(\varphi )\), \(u_{4t}(\varphi ))\)\(\in X^{+}\) for all \(t\ge 0;\)
-
(ii)
For initial value \(\varphi \in X^{+}\), system (2) admits a unique nonnegative bounded solution \({\hat{u}}(t, \varphi )\) on \([0, \infty )\) with \({\hat{u}}_{0}=\varphi \), and \({\hat{u}}_{t}(\varphi ):=({\hat{u}}_{1t}(\varphi )\), \({\hat{u}}_{2t}(\varphi )\), \({\hat{u}}_{3t}(\varphi )\), \({\hat{u}}_{4t}(\varphi ))\)\(\in X^{+}\) for all \(t\ge 0;\)
-
(iii)
For initial value \(\varphi \in U\), system (3) admits a unique nonnegative bounded solution \(v(t, \varphi )\) on \([0, \infty )\) with \(v_{0}=\varphi \), and \(v_{t}(\varphi ):=(v_{1t}(\varphi )\), \(v_{2t}(\varphi )\), \(v_{3t}(\varphi ))\)\(\in U\) for all \(t\ge 0.\)
Proof
We only prove (i) here as (ii) and (iii) can be established by similar arguments. For any \(\varphi =(\varphi _{1},\varphi _{2},\varphi _{3},\varphi _{4})\in X^{+}\), we define
Since \(f(t,\varphi )\) is continuous in \((t, \varphi ) \in R^{+} \times X^{+}\), and \(f(t,\varphi )\) is Lipschitz in \(\varphi \) on each compact subset of \(X^{+}\), then it follows from Theorems 2.2.1 and 2.2.3 in Hale and Lunel (1993), system (1) has a unique solution \(u(t, \varphi )\) on its maximal existence interval \([0, \sigma _{\varphi })\) with \(u_{0}=\varphi \).
Let \(\varphi \in X^{+}\) be given. It is easy to verify that if \(\varphi _{i}(0)=0\) for some \(i \in \{1,2,3,4\},\) then \(f_{i}(t, \varphi ) \ge 0.\) This together with Theorem 5.2.1 and Remark 5.2.1 in Smith (1995) imply the unique solution \(u(t, \varphi )\) remains nonnegative for all \(t\in [0, \sigma _{\varphi }).\)
Set \(\rho (t):=u_{1}(t)+u_{2}(t)+u_{3}(t)\). Note from (1) that \(\rho '(t)=\varLambda -d\rho (t)\), which implies \(\lim _{t\rightarrow \infty }\rho (t)= \frac{\varLambda }{d}\). Thus \(u_{1}(t), u_{2}(t)\) and \(u_{3}(t)\) are bounded on \([0, \sigma _{\varphi })\). Hence, by the last equation of (1), \(u_{4}(t)\) is also bounded on \([0, \sigma _{\varphi })\). In view of Theorem 2.3.1 in Hale and Lunel (1993), we have \(\sigma _{\varphi }=\infty .\)\(\square \)
3 Basic Reproduction Number and Threshold Dynamics of Disease
The basic reproduction ratio \({\mathcal {R}}_{0}\), defined as the expected average number of secondary cases produced in a completely susceptible population by a typical infective individual during the infectious period, is one of the most significant concepts in population biology (Diekmann et al. 1990; Anderson and May 1991; van den Driessche and Watmough 2002; Zhao 2017). In epidemiology, \({\mathcal {R}}_{0}\) is also a commonly used measure of the effort needed to control an infectious disease. In this section, we will calculate the basic reproduction number \({\mathcal {R}}_{0}\) of system (1) and investigate the threshold dynamics in terms of \({\mathcal {R}}_{0}\).
It is easy to calculate the disease-free equilibrium of system (1) \({\hat{E}}_{0}=({\bar{N}},0,0,0)\). Note that \({\hat{E}}_{0}\) is also the disease-free equilibrium of system (2). In view of Zhao (2017) Corollary 11.1.1, the basic reproduction number for the functional differential equations (1) can be denoted by
The Jacobian matrix associated with the linearization of system (1) at \({\hat{E}}_{0}\) is
Therefore, the characteristic equation of \({\hat{E}}_{0}\) gives
This implies that the disease-free equilibrium \({\hat{E}}_{0}\) of system (1) is local asymptotically stable if \({\mathcal {R}}_{0}<1\) and unstable if \({\mathcal {R}}_{0}>1\). Now we proceed to the global asymptotically stability of \({\hat{E}}_{0}\) for system (1).
Theorem 2
-
(i)
The disease-free equilibrium, denoted by \(E_{0}=(0,0,0)\), of system (3) is globally asymptotically stable if \({\mathcal {R}}_{0}\le 1\) and unstable if \({\mathcal {R}}_{0}>1\);
-
(ii)
The disease-free equilibrium \({\hat{E}}_{0}\) of system (2) ( or system (1) ) is globally asymptotically stable if \({\mathcal {R}}_{0}\le 1\) and unstable if \({\mathcal {R}}_{0}>1\).
Proof
We prove (i) by constructing a Lyapunov functional and applying LaSalle’s invariance principle (Theorem 1 in Hale 1969; Theorem 1.1.1 in Zhao 2017) for infinite-dimensional dynamical systems. It is easy to verify that system (3) defines a dynamical system on U. Let Q(t) be the solution semiflow of system (3) on U, i.e., \(Q(t)\varphi =v_{t}(\varphi )\), \(t\ge 0,\) where \(v(t,\varphi )\) is the unique solution of system (3) with \(v_{0}=\varphi \). By Theorem 3.6.1 in Hale and Lunel (1993), Q(t) is continuous and compact, and for each \(\varphi \in U\), the orbit of \(\varphi \) under Q(t) has compact closure in U.
For any \(\phi \in U\), define the functional
For an arbitrary solution \(v(t, \varphi )\) of (3), we obtain
Therefore, \(\frac{\mathrm{d}}{\mathrm{d}t}L(v_{t}(\varphi ))\le 0\), which implies that \(L(\phi )\) is a Lyapunov functional on U relative to the system (3).
Next define
where \(v(t, \varphi )\) is the unique solution of (3) with initial condition \(v_{0}=\varphi \in U\). By (5), we have \({\mathcal {S}}=\{\varphi \in U|\varphi _{2}=0 \}.\) It follows from (3) that the maximal invariant set in \({\mathcal {S}}\) is given by
Thus by the LaSalle invariant principle (Theorem 1 in Hale 1969), we obtain \(\lim _{t\rightarrow \infty } E(t), I(t)=0,\) which together with (3) imply \(\lim _{t\rightarrow \infty } M(t)=0.\)
Now we prove (ii). Let \(\varPsi (t)\) be the solution semiflow of system (2) on \(X^{+}\), i.e., \(\varPsi (t)\varphi ={\hat{u}}_{t}(\varphi )\), \(t\ge 0,\) where \({\hat{u}}(t,\varphi )\) is the unique solution of system (2) with \({\hat{u}}_{0}=\varphi \). By Theorem 3.6.1 in Hale and Lunel (1993), \(\varPsi (t)\) is continuous and compact. For any given \(\varphi \in X^{+}\), let \(\omega (\varphi )\) be the omega limit set of the orbit for the semiflow \(\varPsi (t).\)
Note from the first equation of (2) that \(\omega (\varphi )=\{{\bar{N}}\}\times {\tilde{\omega }}\), where \({\tilde{\omega }}\) is a subset of \(Y^{+}\). It is easy to verify that \({\tilde{\omega }} \subset U\). By Lemma 1.2.1 in Zhao (2017), \(\omega (\varphi )\) is an internally chain transitive set for \(\varPsi (t)\) on \(X^{+}\). It then follows \({\tilde{\omega }}\) is an internally chain transitive set for Q(t) on U. Note from (i) that \(E_{0}\) is globally asymptotically stable for Q(t) on U. It follows from Theorem 1.2.1 in Zhao (2017) that \(\omega (\varphi )=\{{\hat{E}}_{0}\}\). Thus we have completed the proof (ii), and then the disease-free equilibrium system (1) can be directly obtained. \(\square \)
Now we show the disease will be persistent if \({\mathcal {R}}_{0}>1\). Let \(\varPhi (t)\) be the solution semiflow of system (1) on \(X^{+}\), i.e., \(\varPhi (t)\varphi =u_{t}(\varphi )\), \(t\ge 0,\) where \(u(t,\varphi )\) is the unique solution of system (1) with \(u_{0}=\varphi \).
Theorem 3
If \({\mathcal {R}}_{0}>1\), then \(\varPhi (t):X^{+} \rightarrow X^{+}\), is uniform persistent with respect to \((X_{0},\partial X_{0})\), where \(X_{0}=\{\varphi \in X^{+} |\varphi _{2}(0)\ne 0 \ \ \text {and} \ \ \varphi _{3}(0)\ne 0\}, \partial X_{0}=X^{+} \backslash X_{0}\) , i.e., there exists a positive constant \(\eta >0\) such that
Besides, system (1) admits a unique endemic equilibrium, denoted by \({\hat{E}}_{1}=({\bar{N}}-{\hat{E}}-{\hat{I}}, {\hat{E}}, {\hat{I}}, {\hat{M}})=( {\bar{N}}-(d+\gamma ){\hat{I}}/\sigma -{\hat{I}}, (d+\gamma ){\hat{I}}/\sigma , \ {\hat{I}}, \ \delta {\hat{I}}/\mu )\), where
and Lambert W(.) is a Lambert W function, defined to be the multivalued inverse of the function \(\omega \rightarrow \omega e^{\omega }\) (Corless et al. 1996).
Proof
We appeal to the uniform persistence theory developed in Zhao (2017), Magal and Zhao (2005). Note that \(X^{+}=X_{0}\cup \partial X_{0}\). Moreover, \(X_{0}\) and \(\partial X_{0}\) are relatively open and closed subsets of \(X^{+}\), respectively, and \(X_{0}\) is convex. It follows from Hale and Lunel (1993) Theorem 3.6.1 that \(\varPhi (t)\) is continuous and compact for all \(t>0\). In view of Theorem 1, \(\varPhi (t)\) is point dissipative. Therefore \(\varPhi (t)\) has a global attractor by Theorem 2.4.7 in Hale (1988).
Step 1. We have \(\varPhi (t)X_{0} \subset X_{0}\) for all \(t\ge 0\).
Let \(\varphi \in X_{0}\), then we have \(\varphi _{i}(\theta ) \ge 0\) for all \(\theta \in [-\tau , 0], i=\{1,2,3,4\}\), and \(\varphi _{2}(0), \varphi _{3}(0)>0\). It follows from model (3) that
Thus we have \(E(t)\ge \varphi _{2}(0)e^{-(d+\sigma )t}> 0, \ \ I(t)\ge \varphi _{3}(0)e^{-(d+\gamma )t}> 0\).
Step 2. Let \(\omega (x)\) be the \(\omega \)-limit set of \(x \in X^{+}\) with respect to \(\varPhi (t)\). Define
More details about the definitions can be found in Zhao (2017) Chapter 1. It is easy to verify that \(M_{\partial }=\{\varphi \in X^{+} \mid \varphi _{2}=\varphi _{3}=0\}\). Then if \(E(t)=I(t)=0\), for all \(t \ge 0\), we have \({\dot{S}}=\varLambda -dS, {\dot{M}}=-\mu M\). Therefore, \(\varOmega (M_{\partial })=\{{\hat{E}}_{0}\}\). Hence, \(\varOmega (M_{\partial })\) is a compact and isolated invariant set for \(\varPhi (t)\) restricted in \(M_{\partial }.\)
Step 3. We prove \(W^{S}({\hat{E}}_{0})\bigcap X_{0}\) is an empty set by contradiction, where \(W^{S}(A)\) is defined as the stable set of \(A \subset X^{+}\).
Assume, on the contrary, that for any \(\epsilon _{1}>0\), there exists some initial value \(\phi \in X^{+}\) such that
Choose \(\epsilon _{1}\) such that \({\hat{R}}_{0}=\frac{\sigma \beta e^{-\alpha \epsilon _{1}}({\bar{N}}-\epsilon _{1})}{(d+\gamma )(d+\sigma )}>1\). Then there exists \(t_{0}=t_{0}(\epsilon _{1})>0\) such that \({\bar{N}}-\epsilon _{1}<S(t)< {\bar{N}}+\epsilon _{1}, E(t)<\epsilon _{1}, I(t)<\epsilon _{1}, M(t)<\epsilon _{1}\) for all \(t\ge t_{0}\). It follows from Eq. (1) that, for \(t>t_{0}+\tau _{2}\), we have
Let (y(t), x(t)) be the solution of the following cooperative system:
with the initial value \( y(t_{0}+\tau _{2})=E(t_{0}+\tau _{2}), x(t_{0}+\tau _{2})=I(t_{0}+\tau _{2})\). Then we have \(E(t)>y(t), \ \ I(t)>x(t)\) for all \(t> t_{0}+\tau _{2}\). Note that the solution (y(t), x(t)) tends to infinity, which consequently indicates that E(t) and I(t) will approach to the infinity. This contradicts to the above-mentioned arguments. In view of Theorem 1.3.1 and Remark 1.3.1 in Zhao (2017), we have \(\varPhi (t):X^{+} \rightarrow X^{+}\) is uniform persistent with respect to \((X_{0},\partial X_{0})\).
Let \({\hat{E}}_{1}=({\hat{S}}, {\hat{E}},{\hat{I}},{\hat{M}})\) be the endemic equilibrium. By system (1), we obtain
Rewriting this equation gives
Therefore, \({\hat{I}}=\frac{\sigma {\bar{N}}}{d+\gamma +\sigma }-\frac{\mu }{\alpha \delta } LambertW(e^{\frac{\alpha \delta \sigma {\bar{N}}}{\mu (d+\gamma +\sigma )}}\frac{\alpha \delta (d+\sigma )(d+\gamma )}{\mu \beta (d+\gamma +\sigma )})\) (see details for LambertW function in paper Corless et al. 1996). Besides, it is easy to verify that \({\hat{I}}>0\) if and only if \({\mathcal {R}}_{0}>1\). \(\square \)
4 Dynamics at the Endemic Equilibrium Without Delays
In this section, we assume \(\tau _{1}=\tau _{2}=0\), then system (1) becomes
and the limiting system (3) becomes
Obviously, \({\hat{E}}_1\) is also the unique endemic equilibrium of system (8). Moreover, system (9) admits a unique endemic equilibrium, denoted by \(E_{1}=((d+\gamma ){\hat{I}}/\sigma , \ {\hat{I}}, \ \delta {\hat{I}}/\mu )\), where \({\hat{I}}\) is defined in (6).
For further purposes, we first give a preliminary result.
Lemma 1
Assume that \(k, m>0\) and \(r>1\). Let m, r be fixed and denote the unique positive root of \(f(x)=re^{-kx}(1-mx)-1=0\) by \(x_{0}=g(k)\). Set \(h(k)=kg(k)\). Then we have:
-
(i)
\(g'(k)<0, \ \ \lim _{k\rightarrow 0}g(k)=\frac{r-1}{mr}, \ \ \lim _{k\rightarrow \infty }g(k)=0\);
-
(ii)
\(h'(k)>0, \ \ \lim _{k\rightarrow 0}h(k)=0, \ \ \lim _{k\rightarrow \infty }h(k)=\ln r.\)
Proof
Note that
It follows from \(e^{kx_{0}}=r(1-mx_{0})\) that for any \(k>0\), we have \(0<g(k)<\frac{1}{m}\) and \(0<h(k)<\ln r\). This together with the monotonicity of g(k), h(k) in k implies the existence of limits.
We first prove (i). Note that
Hence, \(\lim _{k\rightarrow 0}g(k)=\frac{r-1}{mr}\). Moreover, we have \(\lim _{k\rightarrow \infty }g(k)=0\), for if it is not true, then
For (ii), it can be seen that
and
Therefore, we complete the proof of (ii). \(\square \)
4.1 Local Stability and Local Hopf Bifurcation at the Endemic Without Delays
In what follows, we will obtain the stability of \({\hat{E}}_{1}\) of system (8) by exploring the stability of \(E_{1}\) with respect to the limiting system (9). Particularly, we fix \({\bar{N}}, \beta , d, \sigma , \mu \) here and set
as the bifurcation parameter to explore whether Hopf bifurcation can occur at \(E_{1}\) or not. Recall that here \(\delta /\mu \) is actually the relative reproduction ratio of mass media due to the reported number of infected individuals at time \(\tau _1\) ago. Thus, \(k=\alpha \delta /\mu \) can be regarded as a parameter to measure the effect of psychological impact of media reported numbers of infectious individuals.
The Jacobian matrix concerned the linearization of system (9) at \(E_{1}\) is
Therefore, the characteristic equation \(|J_\mathrm{{E_{1}}}-\lambda I_{3\times 3}|=0\) yields
where
In view of Hurwitz criterion, we only need to verify the sign of \(a_{2}a_{1}-a_{0}\) to check the stability of endemic equilibrium \(E_{1}\), since \(a_\mathrm{{i}}>0, i=1,2,3 .\) To investigate whether system (9) undergoes Hopf bifurcation at the endemic \(E_{1}\) (details about Hopf bifurcation can be seen in Theorems 3.1 and 3.15 in Marsden and McCracken 1976), we begin with exploring the existence of imaginary roots of the characteristic Eq. (11). Substituting \(\lambda =iw, w\in R^{+}\), into Eq. (11) yields
It follows from (13) that a pair of imaginary roots \(\pm \, iw\) of the characteristic Eq. (11) exists only if there exists \(k>0\) such that \(\varTheta (k):=-\,a_{2}(k)a_{1}(k)+a_{0}(k)=0\). If \(\varTheta (k)=0\), in order to validate the transversality condition of Hopf bifurcation, we need to verify the sign of \(Re(\frac{\mathrm{d}\lambda }{\mathrm{d}k}|_{\lambda =iw})\). We have
Now we study the properties of \(\varTheta (k)\). Note from (12) and \(\beta {\hat{I}} e^{-\alpha {\hat{M}}}=\frac{(d+\gamma )(d+\sigma ){\hat{I}}}{\sigma {\bar{N}}-(d+\gamma +\sigma ){\hat{I}}}:= g({\hat{I}})\) that
By using Lemma 1, which gives estimation of \({\hat{I}}\) with respect to k, we can get the following relations:
By Lemma 1, we obtain that \(g({\hat{I}})\) is monotone decreasing in k, and \(k{\hat{I}}\) is monotone increasing in k. Therefore, \(\varTheta '(k)>0\) and
Denote
Thus by (16), if \(1<{\mathcal {R}}_{0}\le {\mathcal {R}}_{1} \), we have \(\varTheta ({k})<0 \) for any \(k>0\), which by Hurwitz criteria, the endemic equilibrium \(E_{1}\) is locally asymptotically stable. If \({\mathcal {R}}_{0}>{\mathcal {R}}_{1}\), then there exists a unique \(k_{0}\) such that \(\varTheta (k_{0})=0\). Therefore, in view of Theorems 3.1 and 3.15 in Marsden and McCracken (1976), we have the following results.
Theorem 4
-
(i)
If \(1<{\mathcal {R}}_{0}\le {\mathcal {R}}_{1}\), then the endemic equilibrium \(E_{1}\) of system (9) is locally asymptotically stable for any \(k>0\).
-
(ii)
If \({\mathcal {R}}_{0}>{\mathcal {R}}_{1}\), the endemic equilibrium \(E_{1}\) is asymptotically stable for \(k \in [0, k_{0})\) and unstable for \(k>k_{0}\). Besides, system (9) undergoes Hopf bifurcation at the endemic equilibrium when \(k=k_{0}\), where \(k_{0}\) is the unique positive root of \(\varTheta (k)=0\) (given in (14)).
Remark 1
Denote the Jacobian matrix concerned the linearization of system (8) at \({\hat{E}}_{1}\) by \(J_{{\hat{\mathrm{E}}}_{1}}\). It is easy to verify that the characteristic equation
Thus Theorem 4 also holds for \({\hat{E}}_{1}\) in system (8).
We now use numerical results to demonstrate our theoretical results in Theorem 4 (ii). We fixed
Then we have \({\mathcal {R}}_{0}>{\mathcal {R}}_{1}\). We now take \(\delta \) as a flexible parameter, and let \(k=\frac{\alpha \delta }{\mu }\) be the bifurcation parameter. We then obtain that \(k_{0}\approx 384\) in Theorem 4 (ii). Figure 1 shows that the endemic equilibrium is asymptotically stable for \(k=350<k_{0}\approx 384\) (shown in Fig. 1a), and the bifurcated periodic solution is feasible for \(k=400>k_{0}\approx 384\) (shown in Fig. 1b). Note that here relatively large value of parameter k implies very quick mass media’ response and individuals’ response, and further this quick response has more likely to induce the periodic oscillation of disease infections. Moreover, we plotted the bifurcation diagram by using the media impact level k as the bifurcation parameter (shown in Fig. 2). It can be seen from the bifurcation diagram that media coverage lowers the equilibrium level of the disease infection.
Our theoretical and numerical results imply that though the media coverage itself is not a determined fact to eradicate the infection of the disease, the analysis demonstrates that the higher media impact level , the less number of individuals will be infected.
4.2 Global Stability of the Endemic Equilibrium Without Delays
In what follows, we will show directly when \({\mathcal {R}}_{0}>1\) and k is sufficient small, the unique endemic equilibrium \({\hat{E}}_{1}\) of system (8) is globally asymptotically stable, which implies \(E_{1}\) is globally asymptotically stable for limiting system (9). For further purposes, we give the following two lemmas.
Lemma 2
For initial value \(\varphi \in R_{+}^{4}\), system (8) admits a unique nonnegative bounded solution \({\bar{u}}(t, \varphi )\) for all \(t\ge 0\) with \({\bar{u}}_{0}=\varphi \).
Lemma 3
If \({\mathcal {R}}_{0}>1\), there exists a positive constant \(\eta _{0}\) such that for (8)
The proofs of Lemma 2 and Lemma 3 are standard, so we omit here.
Theorem 5
If \({\mathcal {R}}_{0}>1\) and \(k \le \frac{\mu +d}{\mu {\bar{N}}}\), then the unique endemic equilibrium \({\hat{E}}_{1}\) of system (8) is globally asymptotically stable.
Proof
Now we prove that the unique endemic equilibrium of system (8) is globally asymptotically stable by using the theory developed in Li et al. (1999), Li and Muldowney (2000). The Jacobian matrix of system (8) reads
The third additive compound matrix of J is
and the corresponding linear compound system reads
In view of Li et al. (1999), Li and Muldowney (2000), we need to show the uniform global stability of the linear compound system. For this purpose, we choose the Lyapunov functional as
where a will be determined later. It follows from Lemma 2 and 3 that there exist two positive constants \(C_{1}, C_{2}\) such that
Next, we derive the total derivative of V along the trajectory of the linear compound system (20). We will separate the discussion for the several cases below. Throughout the calculation, we denote \(D_{+}\) the right-hand (total) derivative with respect to t and we will use the following equalities:
Case (1): \(V=\frac{a|X|}{E}\), which implies \(\frac{a|X|}{E} \ge \frac{|Y|}{E}, \frac{a|X|}{E}\ge \frac{|Z|+|W|}{I}\). We have
Case (2): \(V=\frac{|Y|}{E}\), which implies \(\frac{|Y|}{E}\ge \frac{a|X|}{E}, \frac{|Y|}{E}\ge \frac{|Z|+|W|}{I}\). We have
Case (3): \(V=\frac{|Z|+|W|}{I}\), which implies \(\frac{|Z|+|W|}{I}\ge \frac{a|X|}{E}, \frac{|Z|+|W|}{I}\ge \frac{|Y|}{E}\). Then,
Since \(\alpha \delta \le \frac{\mu +d}{{\bar{N}}}\), we can choose \(\frac{\delta }{d+\mu }\le a \le \frac{1}{\alpha {\bar{N}}}\) such that \(a\alpha I\le 1\) in case 1) and \(\frac{\delta }{a}\le d+\mu \) in case 2). Therefore, in view of Lemma 2, 3, there exists a positive constant b such that \(D_{+}V\le -b V\). By Li et al. (1999) Corollary 3.2, \({\hat{E}}_{1}\) of the system (8) is globally asymptotically stable. \(\square \)
5 Dynamics of System (3) at the Endemic Equilibrium with Delays
Throughout this section, we assume that \(1<{\mathcal {R}}_{0}\le {\mathcal {R}}_{1}\) or \({\mathcal {R}}_{0}>{\mathcal {R}}_{1}\), \(k=\frac{\alpha \delta }{\mu } \in [0, k_{0})\), where \({\mathcal {R}}_{1}\) is defined in (17) and \(k_{0}\) is the unique positive root of \(\varTheta (k)=0\) (given in (14)). This assumption means the unique endemic equilibrium \(E_{1}\) is locally asymptotically stable when \(\tau :=\tau _{1}+\tau _{2}=0\). In the following, we focus on the effect of time delays on stability of the endemic equilibrium and examining the local and global Hopf bifurcation of system (3) with two time delays.
5.1 Preliminary Results
While dealing with the stability and local Hopf bifurcation of an equilibrium associated with functional differential equations, the properties of characteristic functions corresponding to the linearized functional differential equations, which are called exponential polynomials, are of great significance. We give two properties associated with the existence of purely imaginary roots and the transversality conditions of local Hopf bifurcation, which may be used in other functional equations.
Consider the exponential polynomial
where \(n=2l+1, l\in Z^{+}, \tau \in R^{+}\), \(a_{j}, b_{j}\in R, j=1,2,...,n\) with \(a_\mathrm{{n}}=1, b_\mathrm{{n}}=0\) and
Now we explore the existence of purely imaginary roots \(\pm iw, w>0\) with respect to (21). Substituting \(\lambda = iw\) into \(P(\lambda , \tau )\) yields
and \(P(iw,\tau )=0\) gives \(A_{1}(w^2)^2+w^2A_{2}(w^2)^2=B_{1}(w^2)^2+w^2B_{2}(w^2)^2.\) Set
If w exists, i.e., \(F(x)=0\) admits a positive root \(x=\omega ^2\), then
which implies \(\tau =\tau ^{m}, m=0, 1, 2, 3, \ldots ,\) and
Moreover, we further have the following sign equality:
Lemma 4
\(\mathrm{sign}(Re(\frac{\mathrm{d}\lambda }{\mathrm{d}\tau })|_{\tau =\tau ^{m}})=\mathrm{sign}(\frac{\mathrm{d}F(x)}{\mathrm{d}x}|_{x=w^2})\), where \(\tau ^{m}=\tau ^{0}+\frac{2m\pi }{w}\) and m is an integer.
Proof
It follows from the formula of \(P(\lambda ,\tau )\) defined in (21) that
Moreover, \(P(iw, \tau ^{m})=0\) yields
Therefore, we get
Since \(A_{1}^2+w^2A_{2}^2=B_{1}^2+w^2B_{2}^2\), we have
Since \(B_{1}^2+w^2B_{2}^2\) is positive, we obtain
\(\square \)
5.2 Local Stability and Local Hopf Bifurcation
In what follows, we will investigate the stability of \(E_{1}\) with respect to system (3). Particularly, we now set delay \((\tau _{1},\tau _{2})\in R^{+}\times R^{+}\) as the bifurcation parameters to explore whether Hopf bifurcation can occur at \(E_{1}\) or not.
The Jacobian matrix about the lineralization of system (3) at \(E_{1}\) gives
Thus the characteristic equation of \(E_{1}\) reads
where
It follows from Theorem 4 that \(E_{1}\) is locally asymptotically stable for \(\tau =0\). In view of Ruan and Wei (2003), the stability of \(E_{1}\) may change if a pair of purely imaginary roots \(\lambda =\pm iw, w>0\) arises. Now we use the results in Lemma 4 together with Lemma A.1, A.2, A.3 in Appendix A to check whether system (3) undergoes Hopf bifurcation at the endemic equilibrium \(E_{1}\).
We have \(A_{1}(x)=a_{0}-a_{2}x, \ \ A_{2}(x)=a_{1}-x, \ \ B_{1}(x)=b, \ \ B_{2}(x)=0\) in (22). Moreover, \(P(iw,\tau )=0\) yields
and
Recall the definitions in Appendix A,
If \((p, q, r) \in D_{1}\), we have
and
If \((p, q, r) \in D_{2}\), we have
Moreover, for \(i=1, 2,\)
In view of Lemma 4, A.1, A.2, A.3 and Corollary 2.4 in Ruan and Wei (2003), and applying the Hopf bifurcation theorem for delay differential equations (Theorem 11.1.1 in Hale and Lunel 1993), we have the following theorem.
Theorem 6
Let \((\tau _{1},\tau _{2}) \in R^{+}\times R^{+}\). Assuming \(1<{\mathcal {R}}_{0}\le {\mathcal {R}}_{1}\) or \({\mathcal {R}}_{0}>{\mathcal {R}}_{1}\), \(k=\frac{\alpha \delta }{\mu } \in [0, k_{0})\), where \({\mathcal {R}}_{1}\) is defined in (17) and \(k_{0}\) is the unique positive root of \(\varTheta (k)=0\) (given in (14)).
-
(i)
If \((p, q, r) \in D_{1}\) (defined in (47)), the endemic equilibrium of system (3) is locally asymptotically stable for \(\tau \in [0, \tau ^{0})\) and unstable for \(\tau >\tau ^{0}\). Besides, system (3) undergoes Hopf bifurcation at the endemic equilibrium when \(\tau =\tau ^{m}, m=0,1,2...\), where \(\tau ^{0}\) is given in (29) with \(w=\sqrt{x_{1}}\) (see details in (28));
-
(ii)
If \((p, q, r) \in D_{2}\) (defined in (49)), the endemic equilibrium of system (3) is asymptotically stable for \(\tau \in [0, \tau ^{0})\) and unstable for \(\tau >\tau ^{0}\). Besides, system (3) undergoes Hopf bifurcation at the endemic equilibrium when \(\tau =\tau ^{m,i}, i=1,2, m=0,1,2...\), where \(\tau ^{0,i}, i=1,2,\) are given in (31) with \(w_{i}=\sqrt{x_{i}}\) (see details in (30)) and \(\tau ^{0}=min\{\tau ^{0,1}, \tau ^{0,2}\}\);
-
(iii)
In other cases, the endemic equilibrium of system (3) is locally asymptotically stable.
5.3 Global Hopf Bifurcation
In this section, we explore the continuation and termination of the local Hopf bifurcation emanating from \(\tau =\tau ^{n}, n=1,2,3,...\) for \((p, q, r) \in D_{1}\) (given in (47)), or \(\tau =\tau ^{n,i}, i=1,2, n=1,2, ...\) for \((p, q, r) \in D_{2}\) (given in (49)) by using global Hopf bifurcation theorem of functional differential equations (Theorem 3.2 in Wu 1998; see also Erbe et al. 1992). We refer to Qu et al. (2010), Wei and Li (2005), Shu et al. (2014) for more applications about global Hopf bifurcation theorem of functional differential equations. Throughout this part, we assume that \({\mathcal {R}}_{0}>1\) and \(k\le \frac{\mu +d}{\mu {\bar{N}}}\), which means that the endemic equilibrium \(E_{1}\) of system (3) without time delays is globally asymptotically stable.
Denote \({\mathcal {X}}=C([-1,0],R^{3})\). Let \(\tau _{1}=s\tau , \tau _{2}=(1-s)\tau \), and fix s here. Set \(z(t)=(z_{1}(t),z_{2}(t),z_{3}(t))=(E(\tau t),I(\tau t),M(\tau t))\) and rewrite system (3) as the following functional differential equation:
where \(z_{t}(\theta )=z (t+\theta ), \ \ \theta \in [-1,0]\) , \(z_{t}\in {\mathcal {X}}\) and
\({\tilde{F}}\) denotes the restricted functional of F on \(R^{3} \times R^{+} \times R^{+}\), i.e.,
It is obvious that \({\tilde{F}}\) is twice continuously differentiable. Thus the assumption (A1) in global Hopf bifurcation theorem (Theorem 3.2 in Wu 1998) is corroborated.
Let the set of stationary solutions of system (32) be
For any \(({\tilde{z}},{\tilde{\tau }},{\tilde{T}}) \in N(F)\), we have \(DF({\tilde{z}},{\tilde{\tau }},{\tilde{T}})(e^{-\lambda }Id)\ne 0\), which implies the assumption (A2) in Theorem 3.2 in Wu (1998) is satisfied.
For any stationary solution \(({\tilde{z}},{\tilde{\tau }},{\tilde{T}})\), the characteristic matrix is
Thus the characteristic equation of the stationary solution gives
where
Therefore, the assumption (A3) in Wu (1998) holds true.
In view of Theorem 3.2 in Wu (1998), if \(det(\varDelta _{({\tilde{z}},{\tilde{\tau }},{\tilde{T}})}(im\frac{2\pi }{{\tilde{T}}}))=0\) for some integer m, we call this stationary solution \(({\tilde{z}},{\tilde{\tau }},{\tilde{T}}) \in N(F)\) a center. Moreover, if it is the only center in some neighborhood of \(({\tilde{z}},{\tilde{\tau }},{\tilde{T}})\) and it has finitely purely imaginary characteristic values of the form \(im\frac{2\pi }{{\tilde{T}}}\), we call this center is isolated. Let \(J({\tilde{z}},{\tilde{\tau }},{\tilde{T}})\) denote the set of all such positive integers m. From Wu (1998), we know that for any integer \(n\ge 0\), \((({\hat{E}},{\hat{I}},{\hat{M}}),\tau ^{n},\frac{2\pi }{\omega _{0}\tau ^{n}})\) is an isolated center (see the definitions of \(\tau ^{n}\) and \(\omega _{0}\) in (29), (31), (28), (30) and Theorem 6). Moreover, it has only one purely imaginary eigenvalue of the form \(im\frac{2\pi }{{\tilde{T}}}\) and the only integer \(m=1\). Note that the crossing number in Wu (1998) satisfies
Thus the assumption (A4) in Wu (1998) holds.
Let \(\varSigma (F)=Cl\{(z,\tau ,T): \text{ z } \text{ is } \text{ a } \text{ nontrivial } T\text{-periodic } \text{ solution } \text{ of } \text{ system } (32) \}\) with \(\varSigma (F)\subset {\mathcal {X}}\times R^{+} \times R^{+}\), \(n=1,2,...,\) and \(C(({\hat{E}},{\hat{I}},{\hat{M}}),\tau ^{n},\frac{2\pi }{\omega _{0}\tau ^{n}})\) denotes the connected component of \(({\hat{E}},{\hat{I}},{\hat{M}}),\tau ^{n},\frac{2\pi }{\omega _{0}\tau ^{n}})\) in \(\varSigma (F)\). The global Hopf bifurcation theorem (Theorem 3.2 in Wu 1998) implies that either of the subsequent two assertions holds:
-
(i)
\(C(({\hat{E}},{\hat{I}},{\hat{M}}),\tau ^{n},\frac{2\pi }{\omega _{0}\tau ^{n}})\) is unbounded,
-
(ii)
\(C(({\hat{E}},{\hat{I}},{\hat{M}}),\tau ^{n},\frac{2\pi }{\omega _{0}\tau ^{n}})\) is bounded, \(C(({\hat{E}},{\hat{I}},{\hat{M}}),\tau ^{n},\frac{2\pi }{\omega _{0}\tau ^{n}})\cap N(F)\) is finite and for all \(n=1,2,3,...,\) we have
$$\begin{aligned} \sum _{(z,\tau ,T)\in C(({\hat{E}},{\hat{I}},{\hat{M}}),\tau ^{n},\frac{2\pi }{\omega _{0}\tau ^{n}})\cap N(F)}\gamma _{m}(z,\tau ,T)=0, \end{aligned}$$where \(\gamma _{m}(z,\tau ,T)\) is the mth crossing number of \((z,\tau ,T)\) if \(m \in J(z,\tau ,T)\), otherwise, \(\gamma _{m}(z,\tau ,T)=0\). Theorem 6 implies for each \(n=1,2,...\), \((z,\tau ,T)\in C(({\hat{E}},{\hat{I}},{\hat{M}}),\tau ^{n},\frac{2\pi }{\omega _{0}\tau ^{n}})\),
$$\begin{aligned}&J(z,\tau ,T)=\{1\}, \end{aligned}$$(37)$$\begin{aligned}&\sum _{(z,\tau ,T)\in C\left( ({\hat{E}},{\hat{I}},{\hat{M}}),\tau ^{n},\frac{2\pi }{\omega _{0}\tau ^{n}}\right) \cap N(F)}\gamma _{m}(z,\tau ,T)=\gamma _{1}(z,\tau ,T)=-1<0. \end{aligned}$$(38)Therefore, for all \(n=1,2,...,\) assertion (i) holds, which means the connected component of \((({\hat{E}},{\hat{I}},{\hat{M}}),\tau ^{n},\frac{2\pi }{\omega _{0}\tau ^{n}})\) in \(\varSigma (F)\), \(C(({\hat{E}},{\hat{I}},{\hat{M}}),\tau ^{n},\frac{2\pi }{\omega _{0}\tau ^{n}})\) is unbounded. If its projection onto z-space and T-space are bounded, then the projection on \(\tau \)-space is unbounded. Therefore, we reap the final results of global Hopf bifurcation branches. The following two lemmas help confirm the boundedness of projection of \(C(({\hat{E}},{\hat{I}},{\hat{M}}),\tau ^{n},\frac{2\pi }{\omega _{0}\tau ^{n}})\) onto z-space and T-space. A direct result of Theorem 1 gives the following lemma.
Lemma 5
For initial value \(\phi =(\phi _{1},\phi _{2},\phi _{3})\in \mathcal {X_{+}}\) with \(0<\phi _{1}(0)+\phi _{2}(0)<{\bar{N}}\), all periodic solutions of system (32) are uniformly bounded.
It can be seen from Lemma 5 that the projection of \(C(({\hat{E}},{\hat{I}},{\hat{M}}),\tau ^{n},\frac{2\pi }{\omega _{0}\tau ^{n}})\) onto z-space is bounded. (29) and (31) yield that
If we exclude the existence of periodic solutions of period 1, then system (32) has no periodic solutions of period \(\frac{1}{n}\) for any positive integer n. Then, we can obtain the projection of \(C(({\hat{E}},{\hat{I}},{\hat{M}}),\tau ^{n},\frac{2\pi }{\omega _{0}\tau ^{n}})\) onto T-space is bounded.
Lemma 6
If \({\mathcal {R}}_{0}>1\) and \(k\le \frac{\mu +d}{\mu {\bar{N}}}\), then the system (32) has no periodic solutions of period 1.
Proof
Assume that \(z(t)=(z_{1}(t),z_{2}(t),z_{3}(t))\) is a periodic solution of system (32) with period 1, then \(y(t)=(y_{1}(t),y_{2}(t),y_{3}(t))=(z_{1}(t),z_{2}(t),z_{3}(t-1+s))\) is a periodic solution of the following ordinary differential equation:
By Theorem 5, the endemic equilibrium is globally asymptotically stable and no periodic solutions occur. This contradiction completes the proof. \(\square \)
Theorem 7
Assume that \({\mathcal {R}}_{0}>1\) , \(k\le \frac{\mu +d}{\mu {\bar{N}}}\) and \((p, q, r) \in D_{1} \cup D_{2}\) (see details of \(D_{1}, D_{2}\) in (47), (49)), then for any \(\tau >\tau ^{1}\) system (3) has at least one nontrivial periodic solution, where \(\tau ^{1}=min\{\tau ^{1,1},\tau ^{1,2}\}\) if \((p, q, r) \in D_{2}\).
Proof
Equation (34) implies hypothesis (A1), (A2) and (A3) in Wu (1998) Theorem 3.2 hold true. Moreover, it follows Eqs. (36) and (37) conditions (A4) and (A5) in Wu (1998) Theorem 3.2 hold. By Theorem 6, we know for each \(n=1,2,...\), \((z,\tau ,T)\in C(({\hat{E}},{\hat{I}},{\hat{M}}),\tau ^{n},\frac{2\pi }{\omega _{0}\tau ^{n}})\), and
Thus for all \(n=1,2,...,\)\(C(({\hat{E}},{\hat{I}},{\hat{M}}),\tau ^{n},\frac{2\pi }{\omega _{0}\tau ^{n}})\) is unbounded. Lemma 5 claims the projection of \(C(({\hat{E}},{\hat{I}},{\hat{M}}),\tau ^{n},\frac{2\pi }{\omega _{0}\tau ^{n}}), n=1, 2, 3,...\) onto z-space is bounded. Moreover, (24) yields
In view of Lemma 6, we can exclude the existence of periodic solutions of period 1, which means the projection of \(C(({\hat{E}},{\hat{I}},{\hat{M}}),\tau ^{n}, \frac{2\pi }{\omega _{0}\tau ^{n}})\), \(n=1, 2, 3, ...,\) onto T-space is bounded. Hence, the projection of \(C(({\hat{E}},{\hat{I}},{\hat{M}}),\tau ^{n},\frac{2\pi }{\omega _{0}\tau ^{n}}), n=1, 2, 3,...\) onto \(\tau \)-space is bounded. \(\square \)
By using numerical methods, we depict the local and global Hopf branches of periodic solutions originating from Hopf bifurcation points. We initially fix parameter values as
Here, let \(\tau _{2}=0.5 ({\mathrm{day}})\) and \(\tau _{1}\) vary and consequently \(\tau =\tau _{1}+\tau _{2}\) can be used as the bifurcation parameter. It can be calculated that
Besides, (29) and (28) yield \(\tau ^{0}\approx 22.2,\tau ^{1}\approx 102.1,\tau ^{2}\approx 182\).
It can be observed from Fig. 3a that the endemic equilibrium is asymptotically stable for \(\tau =20<\tau ^{0} \approx 22.2\) and from Fig. 3b that the bifurcated periodic solution is feasible for \(\tau =25>\tau ^{0} \approx 22.2\). By using DDE-BIFTOOL (Engelborghs et al. 2002), we can depict the global Hopf branches of periodic solution originating from Hopf bifurcation points \(\tau ^{0},\tau ^{1},\tau ^{2}\), shown in Fig. 4a. When \(\tau ^{0}<\tau <\tau ^{1}\), system (3) has only one periodic solution originating from \(\tau ^{0}\) and the Hopf branch emanating can continue in a wide range. As \(\tau \) increases and satisfies \(\tau ^{1}<\tau <\tau ^{2}\), we obtain two periodic solutions originating from \(\tau ^{0},\tau ^{1}\). As \(\tau \) further increases and satisfies \(\tau >\tau ^{2}\), three periodic solutions originating from \(\tau ^{0},\tau ^{1},\tau ^{2}\) coexist. It follows from Fig. 4b and Theorem 10.3.2 in Hale and Lunel (1993) that the periodic solution bifurcated from \(\tau ^{0}\) is stable, whereas the periodic solutions bifurcated from \(\tau ^{1}\), \(\tau ^{2}\) are unstable. Further, we plotted the bifurcation diagram by using the delay as the bifurcation parameter (shown in Fig. 4c). We mention here that fixing one delay and varying the other, we get the same bifurcation diagrams. This is evidently due to the fact that two delays always sum up together in analyzing bifurcation [see (25)].
Figure 5 describes the effect of two delays on infectious disease in the early stage. In Fig. 5a, b, we fix one delay and vary the other to see that the smaller the delay of mass media’s or individuals’ response is, the lower and earlier the peak comes, which implies both mass media’s timely report and individuals’ prompt response are significant in lowering disease infection. Moreover, if we fix \(\tau _{2}=5\) (day) and increase \(\tau _{1}\) from 3 to 6, 9, 12, then the peak time increases by \(3.81\%, 17.85\%, 19.90\%\), respectively, and the peak value increases by \(4.46\%, 7.04\%, 8.4\%\), respectively; if we fix \(\tau _{1}=5\) (day) and increase \(\tau _{2}\) from 3 to 6, 9, 12, then the peak time increases by \(5.92\%, 23\%, 41.67\%\), respectively, and the peak value increases \(8.14\%, 13.54\%, 16.28\%\), respectively. This implies that the peak time and the peak value are more sensitive to \(\tau _{2}\) (individuals’ response delay) than delay \(\tau _1\)( mass media’s report delay). Therefore, we can see that individuals’ immediate response is more important than mass media’s response in mitigating disease outbreak .
Note that when doing numerical studies shown in Figs. 1–5, we fixed the total population \({\bar{N}}\) as 1, then I(t) represents the fraction of individuals who are infectious. We focus our model on influenza A(H1N1) pandemic, the mean exposed time \(\frac{1}{\sigma }\) and infectious time \(\frac{1}{\gamma }\) are 2, 4, respectively (Pourbohloul et al. 2010). Generally speaking, transmission rate \(\beta \), reporting rate \(\delta \) and media spontaneous disappearance rate \(\mu \) are usually unknown and need to be estimated (Xiao et al. 2015; Yan et al. 2016; Song and Xiao 2018; Yan et al. 2018), we fixed them as in (18) and (43) to demonstrate the occurrence of bifurcation. It is worth mentioning that we choose the very different values of \(\beta \) (which changes from 80 to 1) to illustrate occurrence of Hopf bifurcation shown in Figs. 1 and 2 and in Figs. 3, 4 and 5 for delay case. In Figs. 1 and 2, Hopf bifurcation happens when k is large and \({\mathcal {R}}_{0}>{\mathcal {R}}_{1}=e^{\frac{\mu (2d+\gamma +\sigma )+(2d+\gamma +\sigma )^{2}}{(d+\gamma )(d+\sigma )}}>e^{4}\), so we choose the relatively large value of \(\beta \) (\(\beta =80\)) to simply illustrate the occurrence of bifurcation.
a Global Hopf branches of \(\tau ^{0}, \tau ^{1}, \tau ^{2}\) with respect to system (3). b The principal Floquet multipliers of periodic solutions on branches of \(\tau ^{0}, \tau ^{1}, \tau ^{2}\). c Bifurcation diagram describing the dynamics of system (3) as \(\tau \) increases. Parameters are fixed as (43) (Color figure online)
Solutions of system (3) when a fixing \(\tau _{2}\) and varying \(\tau _{1}\); b fixing \(\tau _{1}\) and varying \(\tau _{2}\). Here \(\beta =1, {\bar{N}}=1, \sigma =1, d=0.2, \gamma =\delta =\mu =0.1, \alpha =3\) (Color Figure Online)
6 Conclusion and Discussion
It has been widely recognized in the epidemiological literatures that mass media have a great impact on individuals’ behavior changes, and hence significantly influence the spread and outbreak of the infectious diseases. There is evidence showing the existence of time delays of mass media and/or individuals’ response and reported delay (Yan et al. 2016). We then proposed an SIR-type model (Song and Xiao 2018) with a delay media impact and examined global dynamics of the proposed model. To further investigate the delayed media impact on disease infection, we extend our paper (Song and Xiao 2018) by including extra compartment M(t), describing the level of news items, and considering two time delays with one representing the reported delay and the mass media’s response duration, and the other denoting the time for individuals’ response to the current media coverage. Hence, we proposed a functional SEIS-M differential model with two time delays, to examine the delayed media impact on the transmission dynamics of emergent infectious diseases. We took the level of media impact as bifurcation parameter and studied the local bifurcation with respect to the endemic equilibrium of the model without delay. Further, we investigated the local and global bifurcation by considering the summation of two delays as a bifurcation parameter and examined the onset and termination of Hopf bifurcations from a positive equilibrium theoretically and numerically.
We defined the basic reproduction number and showed that \({\mathcal {R}}_{0}\) can serve as a threshold value for the global extinction and uniform persistence of the disease. We proved that when the basic reproduction number \({\mathcal {R}}_{0}\) is less than 1, the disease-free equilibrium of system (1) is globally asymptotically stable which means the disease will go to extinction, while the basic reproduction number \({\mathcal {R}}_{0}\) is greater than 1, disease is uniformly persistent and there exists an endemic equilibrium. In particular, the properties of the LambertW function (Corless et al. (1996)) is utilized to represent the positive equilibrium. Moreover, we find that \({\mathcal {R}}_{0}\) is independent of media impact, similar to the main conclusion in papers (Xiao et al. 2013, 2015; Song and Xiao 2018), which implies media is not a determined fact to influence the global extinction and uniform persistence of the disease. Although the media coverage itself is not a determined fact to eradicate the infection of the disease, our results demonstrate that the higher the media impact level , the less number the infected individuals are.
When considering no delays, we found that the ordinary SEIS-M system (8) exhibits interesting dynamics. If the basic reproduction number \(1<{\mathcal {R}}_{0}\le {\mathcal {R}}_{1}\) or the basic reproduction number \({\mathcal {R}}_{0}>{\mathcal {R}}_{1}\) together with the media impact level \(k=\frac{\alpha \delta }{\mu }<k_{0}\), then the unique endemic equilibrium is locally asymptotically stable; if the basic reproduction number \({\mathcal {R}}_{0}>{\mathcal {R}}_{1}\) and the media impact level \(k>k_{0}\), the unique endemic equilibrium is not stable and Hopf bifurcation at the endemic state of the ordinary SEIS-M system (8) may occur. Particularly, by using the third additive compound system theory developed in Li et al. (1999), Li and Muldowney (2000), we show that when the media impact level is small, the endemic equilibrium of the ordinary SEIS-M system (8) is globally asymptotically stable.
When taking two delays into consideration, we showed that under the condition of \(1<{\mathcal {R}}_{0}\le {\mathcal {R}}_{1}\) or \({\mathcal {R}}_{0}>{\mathcal {R}}_{1}\) together with the media impact level \(k=\frac{\alpha \delta }{\mu }<k_{0}\); if \((p, q, r) \in D_{1}\) [defined in (47)], the endemic equilibrium of system (3) is locally asymptotically stable for summation of two delays \(\tau \in [0, \tau ^{0})\), unstable for \(\tau >\tau ^{0}\) and system (3) undergoes Hopf bifurcation at the endemic equilibrium when \(\tau =\tau ^{k}, k=0,1,2,\ldots \); if \((p, q, r) \in D_{2}\) , the endemic equilibrium of system (3) is asymptotically stable for \(\tau \in [0, \tau ^{0})\), unstable for \(\tau >\tau ^{0}\) and system (3) undergoes Hopf bifurcation at the endemic equilibrium when \(\tau =\tau ^{k,i}, i=1,2, k=0,1,2...\); if \((p, q, r) \in R^3/(D_{2}\cup D_{1})\), the endemic equilibrium of system (3) is locally asymptotically stable. Moreover, we validated the global onset and termination of Hopf bifurcations by employing the global Hopf bifurcation theorem (Wu 1998; Qu et al. 2010; Wei and Li 2005; Shu et al. 2014), and obtained that if \({\mathcal {R}}_{0}>1\) , \(k \le \frac{\mu +d}{\mu {\bar{N}}}\) and \((p, q, r) \in D_{1} \cup D_{2}\), system (3) has at least one nontrivial periodic solution for any \(\tau >\tau _{1}\). The numerical analysis through DDE-BIFTOOL developed by Engelborghs et al. (2002) implied that the Hopf branch emanating from \(\tau _{0}\) can continue in a wide range.
Generally, it is hard to handle the systems with two delays (Adimy et al. 2006; Cooke and van den Driessche 1996; Li and Kuang 2007; Ruan and Wei 2003, 1999), and doing bifurcation analysis remains challenging. It is worth noting that here we can fully investigate the local and global bifurcation of system (1) since two delays, although arising different places in the model equations, always add together in the characteristic equations [see (25)]. Consequently, the sum of two delays can act as a bifurcation parameter in analyzing the local and global bifurcation. In fact, from the viewpoint of epidemiology, it is not easy to find the two delays, denoting the mass media’s response duration and individuals’ response to the current media coverage, actually representing a common delay in the feedback cycle from infection to disease incidence, and hence they both together influence stability of endemic equilibrium. Further, it is interesting to mention that time delay is not unique factor to induce periodic oscillation. System (1) without delays can also occur Hopf bifurcation for some suitable conditions. That is because a feedback cycle, from infection to the level of mass media and back to the disease incidence, does exist in the model formulation and may cause oscillations. Main results indicated that media impact with time delays significantly affected the transmission dynamics of infectious diseases. This may enhance our understanding of the effects of behavior changes during an epidemic or pandemic threat, which helps to promote public health communication strategies and disease mitigation measures.
We point out here that the disease-related death was not included in model (1) since, on one hand, we focused our model on influenza A(H1N1) pandemic, and the disease-induced death rate was small and could be ignored. On the other hand, we compromised here to make bifurcation analysis in Theorems 4 and 5 not too complicated. As can be seen in Appendix A, investigating the existence of positives roots of a cubic equation has been quite complicated.
References
Adimy M, Crauste F, Ruan S (2006) Periodic oscillations in leukopoiesis models with two delays. J Theor Biol 242(2):288–299. https://doi.org/10.1016/j.jtbi.2006.02.020
Anderson RM, May RM (1991) Infectious diseases of humans: dynamics and control. Cambridge University Press, Cambridge
Cooke KL, van den Driessche P (1996) Analysis of an SEIRS epidemic model with two delays. J Math Biol 35(2):240–260. https://doi.org/10.1007/s002850050051
Corless RM, Gonnet GH, Hare DE, Jeffrey DJ, Knuth DE (1996) On the Lambert W function. Adv Comput Math 5(1):329–359
Cui JA, Sun Y, Zhu H (2008a) The impact of media on the control of infectious diseases. J Dyn Differ Equ 20(1):31–53. https://doi.org/10.1007/s10884-007-9075-0
Cui JA, Tao X, Zhu H (2008b) An SIS infection model incorporating media coverage. Rocky Mt J Math 38(5):1323–1334. https://doi.org/10.1216/RMJ-2008-38-5-1323
Diekmann O, Heesterbeek JAP, Metz JAJ (1990) On the definition and the computation of the basic reproduction ratio \(R_0\) in models for infectious diseases in heterogeneous populations. J Math Biol 28(4):365–382. https://doi.org/10.1007/BF00178324
Engelborghs K, Luzyanina T, Roose D (2002) Numerical bifurcation analysis of delay differential equations using DDE-BIFTOOL. ACM Trans Math Softw 28(1):1–21. https://doi.org/10.1145/513001.513002
Erbe L, Krawcewicz W, Gȩba K, Wu J (1992) S1-degree and global Hopf bifurcation theory of functional differential equations. J Differ Equ 98(2):277–298
Fan S (1989) A new extracting formula and a new distinguishing means on the one variable cubic equation. Nat Sci J Hainan Teach Coll 2(2):91–98
Funk S (2010) Modelling the influence of human behaviour on the spread of infectious diseases: a review. J R Soc Interface 7(50):1247–1256
Funk S, Bansal S, Bauch CT, Eames KTD, Edmunds WJ, Galvani AP, Klepac P (2015) Nine challenges in incorporating the dynamics of behaviour in infectious diseases models. Epidemics 10(C):21–25
Hale JK (1969) Dynamical systems and stability. J Math Anal Appl 26(1):39–59
Hale JK (1988) Asymptotic behavior of dissipative systems. American Mathematical Society, Providence
Hale JK, Lunel SMV (1993) Introduction to functional differential equations. Springer, New York
Li J, Kuang Y (2007) Analysis of a model of the glucose-insulin regulatory system with two delays. SIAM J Appl Math 67(3):757–776. https://doi.org/10.1137/050634001
Li MY, Muldowney JS (2000) Dynamics of differential equations on invariant manifolds. J Differ Equ 168(2):295–320. https://doi.org/10.1006/jdeq.2000.3888, special issue in celebration of Jack K. Hale’s 70th birthday, Part 2 (Atlanta, GA/Lisbon, 1998)
Li MY, Muldowney JS, van den Driessche P (1999) Global stability of SEIRS models in epidemiology. Can Appl Math Quart 7(4):409–425
Li Y, Cui JA (2009) The effect of constant and pulse vaccination on SIS epidemic models incorporating media coverage. Commun Nonlinear Sci Numer Simul 14(5):2353–2365. https://doi.org/10.1016/j.cnsns.2008.06.024
Liu R, Wu J, Zhu H (2007) Media/psychological impact on multiple outbreaks of emerging infectious diseases. Comput Math Methods Med 8(3):153–164. https://doi.org/10.1080/17486700701425870
Magal P, Zhao XQ (2005) Global attractors and steady states for uniformly persistent dynamical systems. SIAM J Math Anal 37(1):251–275. https://doi.org/10.1137/S0036141003439173
Mao L (2014) Modeling triple-diffusions of infectious diseases, information, and preventive behaviors through a metropolitan social network—an agent-based simulation. Appl Geogr 50(2):31–39
Marsden JE, McCracken M (1976) The Hopf bifurcation and its applications. Springer, Berlin
Pourbohloul B, Ahued A, Davoudi B, Meza R, Meyers LA, Skowronski DM, Villaseñor I, Galván F, Cravioto P, Earn DJD (2010) Initial human transmission dynamics of the pandemic H1N1 2009 virus in North America. Influ Other Respir Viruses 3(5):215–222
Qu Y, Wei J, Ruan S (2010) Stability and bifurcation analysis in hematopoietic stem cell dynamics with multiple delays. Phys D 239(20–22):2011–2024. https://doi.org/10.1016/j.physd.2010.07.013
Ruan S, Wei J (1999) Periodic solutions of planar systems with two delays. Proc Roy Soc Edinburgh Sect A 129(5):1017–1032. https://doi.org/10.1017/S0308210500031061
Ruan S, Wei J (2003) On the zeros of transcendental functions with applications to stability of delay differential equations with two delays. Dyn Contin Discrete Impuls Syst Ser A Math Anal 10(6):863–874
Shu H, Wang L, Watmough J (2014) Sustained and transient oscillations and chaos induced by delayed antiviral immune response in an immunosuppressive infection model. J Math Biol 68(1–2):477–503. https://doi.org/10.1007/s00285-012-0639-1
Smith HL (1995) Monotone dynamical systems: an introduction to the theory of competitive and cooperative systems. American Mathematical Society, Providence
Song P, Xiao Y (2018) Global Hopf bifurcation of a delayed equation describing the lag effect of media impact on the spread of infectious disease. J Math Biol 76(5):1249–1267. https://doi.org/10.1007/s00285-017-1173-y
Sun C, Yang W, Arino J, Khan K (2011) Effect of media-induced social distancing on disease transmission in a two patch setting. Math Biosci 230(2):87–95. https://doi.org/10.1016/j.mbs.2011.01.005
Tang S, Xiao Y, Yang Y, Zhou Y, Wu J, Ma Z (2010) Community-based measures for mitigating the 2009 H1N1 pandemic in china. PLoS one 5(6):e10–911
Tchuenche JM, Dube N, Bhunu CP, Smith RJ, Bauch CT (2011) The impact of media coverage on the transmission dynamics of human influenza. BMC Public Health 11(1):S5
van den Driessche P, Watmough J (2002) Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci 180:29–48. https://doi.org/10.1016/S0025-5564(02)00108-6
Verelst F, Willem L, Beutels P (2016) Behavioural change models for infectious disease transmission: a systematic review (2010–2015). J R Soc Interface 13(125)
Wang A, Xiao Y (2014) A Filippov system describing media effects on the spread of infectious diseases. Nonlinear Anal Hybrid Syst 11:84–97. https://doi.org/10.1016/j.nahs.2013.06.005
Wei J, Li MY (2005) Hopf bifurcation analysis in a delayed Nicholson blowflies equation. Nonlinear Anal 60(7):1351–1367. https://doi.org/10.1016/j.na.2003.04.002
Wu J (1998) Symmetric functional-differential equations and neural networks with memory. Trans Am Math Soc 350(12):4799–4838. https://doi.org/10.1090/S0002-9947-98-02083-2
Xiao Y, Zhao T, Tang S (2013) Dynamics of an infectious diseases with media/psychology induced non-smooth incidence. Math Biosci Eng 10(2):445–461. https://doi.org/10.3934/mbe.2013.10.445
Xiao Y, Tang S, Wu J (2015) Media impact switching surface during an infectious disease outbreak. Sci Rep 5:7838
Yan Q, Tang S, Gabriele S, Wu J (2016) Media coverage and hospital notifications: correlation analysis and optimal media impact duration to manage a pandemic. J Theor Biol 390:1–13. https://doi.org/10.1016/j.jtbi.2015.11.002
Yan Q, Tang S, Xiao Y (2018) Impact of individual behaviour change on the spread of emerging infectious diseases. Stat Med 37(6):948–969
Zhao XQ (2017) Dynamical systems in population biology, 2nd edn. CMS books in Mathematics/Ouvrages de Mathématiques de la SMC, Springer, Cham. https://doi.org/10.1007/978-3-319-56433-3
Acknowledgements
PS was supported by the China Scholarship Council; YX was supported by the National Natural Science Foundation of China(NSFC, 11631012, 11571273(YX)). The authors would like to thank the referees for many helpful comments, which lead to improvements in Theorems 1–3. The authors would like to thank Prof Xiaoqiang Zhao for his generous help in discussing the theory of the limiting system.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A
Appendix A
In this section, we give some properties for the general cubic equations. Consider the following cubic equation with one variable x:
Set
Note that \(R^3=D_{0}\cup D_{1} \cup D_{2}\). We investigate some properties with respect to \(D_{1}\) and \(D_{2}\).
Lemma A.1
(Shengjin distinguishing means Fan 1989) The cubic equation with one variable x satisfies \(x^3+px^2+qx+r=0\) where \(p, q ,r \in R\). Assume
-
(i)
The cubic equation has a triple real root \(X_{1,2,3}=\frac{-p}{3}\) if and only if \(A=B=0\);
-
(ii)
The cubic equation has one real root \(X_{1}=\frac{-p-\root 3 \of {Y_{1}}-\root 3 \of {Y_{2}}}{3}\) and a pair of conjugate complex roots \(X_{2,3}=\frac{-2p+\root 3 \of {Y_{1}}+\root 3 \of {Y_{2}} \pm \root 3 \of {3}(\root 3 \of {Y_{1}}-\root 3 \of {Y_{2}})}{6}\) with \(Y_{1,2}=Ap+3(\frac{-B\pm \sqrt{B^2-4AC}}{2})\) if and only if \(\varDelta >0\);
-
(iii)
The cubic equation has a single real root \(X_{1}=-p+\frac{B}{A}\) and a double real root \(X_{2,3}=\frac{B}{2A}\) if and only if \(\varDelta =0, A\ne 0\);
-
(iv)
The cubic equation has three real roots \(X_{1}=\frac{-p-2\sqrt{A}cos(\frac{\theta }{3})}{3}\), \( X_{2,3}=\frac{-p+\sqrt{A}(cos(\frac{\theta }{3})\pm sin(\frac{\theta }{3}))}{3}\) with \(\theta =\arccos \frac{2Ap-3B}{2\root 3 \of {A}}\)if and only if \(\varDelta <0\).
Remark
If \(\varDelta =0, A=0\), then \(A=B=0\).
Lemma A.2
We obtain \((p, q, r) \in D_{1}\) if and only if one of the following conditions holds:
-
(i)
Condition 1 (C1): \(\varDelta >0, r<0\);
-
(ii)
Condition 2 (C2): \(r=0, q=0 , p<0\) (which implies \(\varDelta =0, A\ne 0\)) or \(\varDelta =0, A\ne 0, r<0\);
-
(iii)
Condition 3 (C3): \(\varDelta <0, q\le 0\) or \(\varDelta<0, q>0, p>0, r<0\) or \(\varDelta<0, q>0, p<0, r\ge 0\).
Proof
(I) Sufficiency.
If C1 holds, by Lemma A.1, \(\varDelta >0\) implies that \(F(x)=0\) has only one real root \(x_{1}\) and F(x) can be rewritten as \(F(x)=(x-x_{1})(x^2+mx+n)\), where \(m, n \in R\) and \(x^2+mx+n=0\) has no real roots, i.e., \(m^2-4n<0\). Note that \(F(0)=r=-x_{1}n<0\), then \(F(x)=0\) admits only one positive root. Besides, \(F'(x_{1})=x^2+mx+n>0\). In view of the definition of \(D_{1}\) in (45), \((p, q, r) \in D_{1}\).
If C2 holds, in view of Lemma A.1, \(\varDelta =0, A\ne 0\) demonstrates that F(x) has a single real root \(x_{1}\), a double real root \(x_{2}\) and \(F(x)=(x-x_{1})(x-x_{2})^2, x_{1}\ne x_{2}\). For the first situation \(r=0, q=0 , p<0\), F(x) has only one positive root \(x=x_{1}=-p\) and \(F'(-p)=p^2>0\). For the second situation \(r<0\), we have \(x_{1}=-\frac{r}{x_{2}^2}>0\), \(F'(x_{1})=(x-x_{2})^2>0\) and \(F'(x_{2})=0\). It can be seen from the definition of \(D_{1}\) in (45), both situations satisfy that \((p, q, r) \in D_{1}\).
If C3 holds, \(\varDelta <0\) together with Lemma A.1 yields that F(x) has three real roots \(x_{1}>x_{2}>x_{3}\) and \(F(x)=(x-x_{1})(x-x_{2})(x-x_{3})\). It is easy to calculate that \(F'(x_{1})=(x_{1}-x_{2})(x_{1}-x_{3})>0\), \(F'(x_{2})=(x_{2}-x_{1})(x_{2}-x_{3})<0\) and \(F'(x_{3})=(x_{3}-x_{1})(x_{3}-x_{2})>0\). For situation one \(q=x_{1}x_{2}+x_{2}x_{3}+x_{1}x_{3}\le 0\), we have \(x_{1}>0\) and \(x_{3}\le 0\) which yields that \((p, q, r) \in D_{1}\). For if \(x_{1} \le 0\), we have \(q \ge x_{2}x_{3}>0\) or if \(x_{3}\le 0\), we obtain \(q \ge x_{2}x_{1}>0\). For situation two \(q=x_{1}x_{2}+x_{2}x_{3}+x_{1}x_{3}>0, p=-(x_{1}+x_{2}+x_{3})>0, r=-x_{1}x_{2}x_{3}<0\), we can show that \(x_{1}>0\) and \(x_{2}, x_{3}< 0\) which yields that \((p, q, r) \in D_{1}\). \(r<0\) implies that \(x_{1}, x_{2}, x_{3}>0\) or \(x_{1}>0, x_{2}, x_{3}<0\). Since \(p=-(x_{1}+x_{2}+x_{3})>0\), we have \(x_{1}>0, x_{2}, x_{3}<0\). For situation three \(q=x_{1}x_{2}+x_{2}x_{3}+x_{1}x_{3}>0, p=-(x_{1}+x_{2}+x_{3})<0, r=-x_{1}x_{2}x_{3}\ge 0\), it can be showed that \(x_{1}>0\) and \(x_{3}\le 0\) which implies that \((p, q, r) \in D_{1}\). It can be observed from \(r \ge 0\) that \(x_{1}, x_{2}>0, x_{3}\le 0\) or \(x_{1} \le 0, x_{2}, x_{3}<0\). since \(p<0\), we obtain \(x_{1}, x_{2}>0, x_{3}\le 0\).
(II) Necessity.
Note that \(D_{1}=\{(p, q, r) \in D_{1}, \varDelta >0\}\cup \{(p, q, r) \in D_{1}, \varDelta =0\}\cup \{(p, q, r) \in D_{1}, \varDelta <0\}\), where \(\varDelta \) is defined as (46). If \(\varDelta >0\), then it follows Lemma A.1 that \(F(x)=0\) has only one real root \(x_{1}\) and F(x) can be rewritten as \(F(x)=(x-x_{1})(x^2+mx+n)\), where \(m, n \in R\) and \(x^2+mx+n=0\) has no real roots, i.e., \(m^2-4n<0\). By \((p, q, r) \in D_{1}\) together with the definition of \(D_{1}\) in (45), \(r=-x_{1}n<0\).
If \(\varDelta =0\), then \((p, q, r) \in D_{1}\) implies \(A\ne 0\) (see definition in (46)). For if \(A =0\), it follows from Fan (1989) that \(B=0\), then the cubic equation F(x) has a triple real root which contradicts that \((p, q, r) \in D_{1}\). By Lemma A.1, \(\varDelta =0\) and \(A\ne 0\) yield that F(x) has a single real root \(x_{1}\), a double real root \(x_{2}\) and \(F(x)=(x-x_{1})(x-x_{2})^2, x_{1}\ne x_{2}\). Besides, we have \(F'(x_{1})=(x_{1}-x_{2})^2>0\) and \(F'(x_{2})=0\). Thus \((p, q, r) \in D_{1}\) implies \(x_{1}>0\). If \(r=-x_{1}x_{2}^2=0\), then \( q=0 , p<0\). If \(r\ne 0\), then \(r=-x_{1}x_{2}^2<0\).
If \(\varDelta <0\), we now verify that \(q\le 0\) or \(q>0, p>0, r<0\) or \(q>0, p<0, r\ge 0\). To start with \(\varDelta <0\) together with Lemma A.1 yields that F(x) has three real roots \(x_{1}>x_{2}>x_{3}\) and \(F(x)=(x-x_{1})(x-x_{2})(x-x_{3})\). It is easy to calculate that \(F'(x_{1})=(x_{1}-x_{2})(x_{1}-x_{3})>0\), \(F'(x_{2})=(x_{2}-x_{1})(x_{2}-x_{3})<0\) and \(F'(x_{3})=(x_{3}-x_{1})(x_{3}-x_{2})>0\). Therefore, \((p, q, r) \in D_{1}\) implies \(x_{1}>0, x_{3} \le 0\). Note that there exists \(y_{1}>y_{2}\) satisfying \(F'(y_{1})=F'(y_{2})=0\), \(q=3y_{1}y_{2}, p=\frac{-3(y_{1}+y_{2})}{2}\), and \(x_{1}>y_{1}>x_{2}>y_{2}>x_{3}\). If \(y_{1}<0\), we have \(q>0, p>0, r<0\); if \(y_{1}\ge 0 \ge y_{2}\), we obtain \(q\le 0\); if \(y_{1}> y_{2}>0\), we have \(q>0, p<0, r\ge 0\).
Thus we completed the proof. \(\square \)
By the similar arguments as the proof of Lemma A.1, we have the following lemma.
Lemma A.3
We have \((p, q, r) \in D_{2}\) if and only if condition 4 (C4): \(\varDelta<0, r<0, p<0, q>0\) is satisfied.
Now we obtain that
and by Lemma A.1, this positive root
where \(Y_{1,2}=Ap+3(\frac{-B\pm \sqrt{B^2-4AC}}{2})\) and A, B, C are defined in (46). Moreover, we have
and by Lemma A.1, the two positive roots are
where A, B, C are defined in (46).
Rights and permissions
About this article
Cite this article
Song, P., Xiao, Y. Analysis of an Epidemic System with Two Response Delays in Media Impact Function. Bull Math Biol 81, 1582–1612 (2019). https://doi.org/10.1007/s11538-019-00586-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11538-019-00586-0