A Model of $\hbox {Ca}^{2+}$ Dynamics in an Accurate Reconstruction of Parotid Acinar Cells

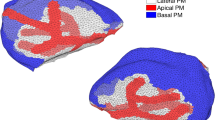
Abstract

We have constructed a spatiotemporal model of $\hbox {Ca}^{2+}$ dynamics in parotid acinar cells, based on new data about the distribution of inositol trisphophate receptors (IPR). The model is solved numerically on a mesh reconstructed from images of a cluster of parotid acinar cells. In contrast to our earlier model (Sneyd et al. in J Theor Biol 419:383–393. https://doi.org/10.1016/j.jtbi.2016.04.030, 2017b), which cannot generate realistic $\hbox {Ca}^{2+}$ oscillations with the new data on IPR distribution, our new model reproduces the $\hbox {Ca}^{2+}$ dynamics observed in parotid acinar cells. This model is then coupled with a fluid secretion model described in detail in a companion paper: A mathematical model of fluid transport in an accurate reconstruction of a parotid acinar cell (Vera-Sigüenza et al. in Bull Math Biol. https://doi.org/10.1007/s11538-018-0534-z, 2018b). Based on the new measurements of IPR distribution, we show that Class I models (where $\hbox {Ca}^{2+}$ oscillations can occur at constant [$\hbox {IP}_3$]) can produce $\hbox {Ca}^{2+}$ oscillations in parotid acinar cells, whereas Class II models (where [$\hbox {IP}_3$] needs to oscillate in order to produce $\hbox {Ca}^{2+}$ oscillations) are unlikely to do so. In addition, we demonstrate that coupling fluid flow secretion with the $\hbox {Ca}^{2+}$ signalling model changes the dynamics of the $\hbox {Ca}^{2+}$ oscillations significantly, which indicates that $\hbox {Ca}^{2+}$ dynamics and fluid flow cannot be accurately modelled independently. Further, we determine that an active propagation mechanism based on calcium-induced calcium release channels is needed to propagate the $\hbox {Ca}^{2+}$ wave from the apical region to the basal region of the acinar cell.

Appendix: Construction of the Finite-Element Mesh

In this appendix, we describe how we used experimentally measured optical slices to construct a multicellular finite-element mesh, in which the cells have conformal intercellular faces. Our work flow has three sequential steps:

• 1. Image segmentation

• 2. Surface triangulation and refinement

• 3. Volumetric meshing

1.1 Image Segmentation

By visual inspection, we identified and selected a contiguous clump of seven cells within our source data image stack. This clump spanned thirty of the images and covered a maximum of approximately one-quarter of each image. Segmentation was done manually by tracing the outline of each cell in each image with a distinct colour, followed by matched colour flood-fill. One-quarter of original image number 16, along with its segmentation, is shown in Fig. 17.

Fig. 17

Subsection of a microscopy image slice on the left and its segmentation on the right (Color figure online)

Note that with our image stack the ratio of stack spacing to pixel resolution is 11.6 (being 0.069 / 0.80). To bring this closer to a one-to-one ratio, we reduced the X and Y dimensions in the segmented image stack by a factor of four using nearest neighbour interpolation (to retain the distinct colouring of each cell) resulting in a pixel spacing of approximately $0.28\upmu \text {m}$. The reduced images were then combined into a single XYZ TIFF stack for convenience.

1.1.1 Curvature

We also wanted to extract some information from the segmented image stack about the smoothness of the surface of each cell. We chose line curvature as a surface smoothness characteristic indicator (Rugis 2005; Rugis and Klette 2006a, b).

To calculate the curvature, we used the $1024 \times 1024$ segmented images and extracted pixels associated with the closed curve boundary outline for each cell in each image, then selected the outline containing the maximum number of pixels for each cell as being the closest to a “great arc” slice through that cell. This great arc criterion was based on the fact that only the curvature associated with a great arc of a sphere is equal to the sphere surface mean curvature.

Next, considering that fact that image pixels are all located on a regular rectangular grid (not very useful for calculating actual local curvature!), a smoothed version of each cell outline was created using a 2D Savitzky–Golay (least-squares) fitting filter (Savitzky and Golay 1964). Figure 18 shows a sample cell outline with the original pixel locations as well as the smoothing process result.

Fig. 18

A sample segmentation pixel outline in green with smoothed node points in red (Color figure online)

Planar line curvature was calculated at each point on the smoothed outlines. We used weighted histograms to visualise the curvature distribution for each of the seven cells. Two of the histograms are shown in Fig. 19. Note that in both cases the curvature distribution is biased towards the positive, as would be expected with any closed curve from the outside using the convention that positive curvature is associated with convex line segments.

Fig. 19

Reference curvature histograms for two of the cells (in $\upmu \text {m}^{-1}$). The distributions are “near normal” (Color figure online)

To simplify our characterisation of cell surface shape, we chose the weighted standard deviation of the curvatures for each cell as a single valued characterisation of surface smoothness and, in that sense, a signature for the shape of each cell. This signature is indicative (i.e. not unique) because standard deviation is only an unambiguous characterisation given normally distributed data. The weighted curvature standard deviation for each of the seven cells is shown in Table 2.

Table 2 The standard deviation of curvature values for seven cells extracted from the microscopy image stack

Fig. 20

Rough multi-domain surface mesh: all seven cells (left) and three exposed cells (right) (Color figure online)

Fig. 21

Cell smoothing evolution, with and without inter-cell coupling (Color figure online)

1.2 Surface Triangulation and Refinement

For the surface triangulation and refinement process, we started with the reduced XYZ TIFF image stack described in the previous section. We treated this reduced stack as a $256\times 256 \times 31$ solid voxel block within which each voxel is labelled with a colour associated with the cell that it belongs to.

1.2.1 Surface Triangulation

Significant prior work in extracting triangle surface meshes from labelled voxel blocks has been done by Boltcheva et al. (2009), and we used their technique. Sample computer code implementing this technique was found on the Computational Geometry Algorithms Library (CGAL) web site (www.cgal.org). Note that we needed to convert our voxel block data to Inria format (www.inria.fr) before passing it to the CGAL code.

The output from the CGAL code was a multi-domain triangle surface mesh, as shown in Fig. 20, where each of the cell faces are labelled in colour by cell. However, there are two problems with this mesh: there are “steps” as a result of the relatively limited stack resolution and, on close inspection, the surfaces are rather rough (as can be seen more clearly in the cell labelled “no smoothing” in the top of Fig. 21). This lack of surface smoothness has the net effect of increasing the surface area of each cell to a value larger than what it most likely is in the real cells.

1.2.2 Surface Smoothing

To reduce the surface area closer to what it should be, we used a constrained surface smoothing process. Note that the smoothing process should: 1) minimise the surface area of each cell, 2) maintain the volume of each cell, and 3) keep the shared conformal faces between cells as being shared.

A pseudo-code outline for our iterative smoothing process is as follows:

For each cell we used the curvature-flow based smoothing operation described in Desbrun et al. (1999). Note that the cell smoothing process works by slightly moving the position of the surface mesh vertices for each cell in turn (with no new faces added or any faces removed). Therefore, vertices associated with shared faces get moved twice in each pass through the Main Loop, i.e. once for each cell in every adjacent pair of cells. In this sense, the smoothing is a coupled process. With our approach, if the vertices associated with shared faces were allowed to split from each other, the result would be non-coupled as shown in the middle row of Fig. 21, which is not what is required.

Coupled smoothing results after each of 6, 16, 40 and 100 iterations are shown in the bottom row of Fig. 21. The question remains: After how many iterations should we stop? This is where we found the weighted curvature standard deviation values from Table 2 useful as will be described in the next section.

1.2.3 Iteration Termination

Recall from the previous section that reducing cell surface area while at the same time maintaining cell volume was an important consideration. The smoothing step in our process has the effect of reducing surface area as shown for one hundred iterations in the left-hand side of Fig. 22. The greatest rate of surface area reduction occurs within the first ten iterations or so. Cell volume is explicitly restored in our process, and thus remains almost unchanged, as can be seen in the right-hand side of Fig. 22. For further guidance as to when to terminate the iterative process, we looked to surface curvature.

Fig. 22

Cell surface area and volume evolution over one hundred coupled smoothing iterations. (Note the much smaller scale range with the plot on the right.) (Color figure online)

For each cell, in every iteration, we calculated the 2D surface curvature at every mesh vertex. Additionally, for each cell, in every iteration, we calculated the weighted standard deviation of those curvatures to get a single smoothness characteristic value. We then compared this value to the associated target standard deviation in Table 2 and expressed it as a ratio as shown in Fig. 23.

Fig. 23

All of the cells hit the target curvature standard deviation ratio of one after nine iterations (Color figure online)

Fig. 24

Initial surface curvature distribution in brown and smoothed surface curvature in blue (Color figure online)

With this information in hand, we decided to terminate the iterative process and accept the results after ten iterations by which time all of the cells had more than dropped below their target characteristic curvature.

Fig. 25

Fully meshed smoothed cells: three exposed cells (left) and all seven cells (right) (Color figure online)

For further insight and confirmation of our results, we produced initial and final iteration weighted surface curvature histograms for each of the seven cells. Histograms for two of the cells are shown in Fig. 24. Note that in all cases, as expected, the initial curvature spread was relatively wide and the final curvature distribution narrower, peaking just to the right (positive) side of zero. The final curvature histograms compared favourably to those associated with the image stacks including those shown earlier in Fig. 19.

1.3 Volumetric Meshing

In the final step of our process, we filled in the surface mesh for each cell with tetrahedrons using the Gmsh software tool (Geuzaine and Remacle 2009). This volumetric meshing employed a 3-D Delaunay refinement algorithm that reduces the instance of tetrahedral slivers, making the tetrahedrons more equilateral, thereby improving the mesh quality from the point of view of the finite-element method. Note that the volumetric meshing did not alter the associated surface meshes, insuring that the meshes remained conformal. Fully meshed cells are shown in Fig. 25.