Connecting Local and Global Sensitivities in a Mathematical Model for Wound Healing

Abstract

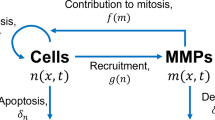
The process of wound healing is governed by complex interactions between proteins and the extracellular matrix, involving a range of signaling pathways. This study aimed to formulate, quantify, and analyze a mathematical model describing interactions among matrix metalloproteinases (MMP-1), their inhibitors (TIMP-1), and extracellular matrix in the healing of a diabetic foot ulcer. De-identified patient data for modeling were taken from Muller et al. (Diabet Med 25(4):419–426, 2008), a research outcome that collected average physiological data for two patient subgroups: “good healers” and “poor healers,” where classification was based on rate of ulcer healing. Model parameters for the two patient subgroups were estimated using least squares. The model and parameter values were analyzed by conducting a steady-state analysis and both global and local sensitivity analyses. The global sensitivity analysis was performed using Latin hypercube sampling and partial rank correlation analysis, while local analysis was conducted through a classical sensitivity analysis followed by an SVD-QR subset selection. We developed a “local-to-global” analysis to compare the results of the sensitivity analyses. Our results show that the sensitivities of certain parameters are highly dependent on the size of the parameter space, suggesting that identifying physiological bounds may be critical in defining the sensitivities.

Appendix

1.1 Steady-State Analysis

Equations (11–14) were first rewritten to be functions of the states present in the equations,

$$\begin{aligned} \frac{{\mathrm {d}}M}{{\mathrm {d}}t}&= p(M,T,f), \end{aligned}$$

(22)

$$\begin{aligned} \frac{{\mathrm {d}}T}{{\mathrm {d}}t}&= q(M,T,f), \end{aligned}$$

(23)

$$\begin{aligned} \frac{{\mathrm {d}}E}{{\mathrm {d}}t}&= r(M,E,f), \end{aligned}$$

(24)

$$\begin{aligned} \frac{{\mathrm {d}}f}{{\mathrm {d}}t}&= s(f). \end{aligned}$$

(25)

The steady states, denoted by ${\overline{\mathbf{x}}} = (\overline{M},\overline{T},\overline{E},\overline{f})$, are the solutions to Eqs. (22–25) when the derivatives are set to 0. Only nonnegative solutions were considered. The stability of each steady state was determined by computing the eigenvalues of the Jacobian matrix (26) evaluated at the steady state.

$$\begin{aligned} J_1(\overline{M},\overline{T},\overline{E},\overline{f}) = \begin{bmatrix} \dfrac{\partial p}{\partial M}&\dfrac{\partial p}{\partial T}&\dfrac{\partial p}{\partial E}&\dfrac{\partial p}{\partial f} \\ \dfrac{\partial q}{\partial M}&\dfrac{\partial q}{\partial T}&\dfrac{\partial q}{\partial E}&\dfrac{\partial q}{\partial f} \\ \dfrac{\partial r}{\partial M}&\dfrac{\partial r}{\partial T}&\dfrac{\partial r}{\partial E}&\dfrac{\partial r}{\partial f} \\ \dfrac{\partial s}{\partial M}&\dfrac{\partial s}{\partial T}&\dfrac{\partial s}{\partial E}&\dfrac{\partial s}{\partial f} \end{bmatrix}. \end{aligned}$$

(26)

Evaluating (26) results in a matrix whose only nonzero element in the third column is $\partial r/\partial E$ and only nonzero element in the fourth row is $\partial s/\partial f$. Therefore, the eigenvalues of (26) are the two partial derivatives and the eigenvalues of the $2 \times 2$ block matrix in the upper left-hand corner,

$$\begin{aligned} J_2(\overline{M},\overline{T},\overline{E},\overline{f})&= \begin{bmatrix} \dfrac{\partial p}{\partial M}&\dfrac{\partial p}{\partial T} \\ \dfrac{\partial q}{\partial M}&\dfrac{\partial q}{\partial T} \end{bmatrix} \nonumber \\&= \left[ \begin{array}{lll} -k_3 - k_4\overline{T} + \dfrac{3k_1k_2^3\overline{f}\overline{M}^2}{(k_2^3+\overline{M}^3)^2} &{}\qquad \qquad \qquad -k_4\overline{M} \\ -k_4\overline{T} + \dfrac{k_5\overline{f}\overline{T}^3}{k_6^3+\overline{T}^3} &{} -k_7 - k_4\overline{M} + \dfrac{3k_5k_6^3\overline{f}\overline{M}\overline{T}^2}{(k_6^3+\overline{T}^3)^2} \end{array}\right] . \end{aligned}$$

(27)

From Eqs. (24, 25),

$$\begin{aligned} \overline{E}= & {} \frac{\overline{f}k_8}{k_{10}+\overline{f}k_8+k_9\overline{M}}, \end{aligned}$$

(28)

$$\begin{aligned} \overline{f}= & {} 0 \text { or } \frac{k_{11}-k_{12}}{k_{11}} . \end{aligned}$$

(29)

We note that for any $\overline{M}$ and $\overline{f}$,

$$\begin{aligned} \frac{\partial r}{\partial E} = -k_{10}-\overline{f} k_8- k_9\overline{M} < 0. \end{aligned}$$

(30)

The derivative

$$\begin{aligned} \frac{\partial s}{\partial f} = (1-\overline{f}) k_{11}-\overline{f} k_{11}-k_{12} \end{aligned}$$

(31)

will be looked at in the proceeding cases. Nonzero solutions for $\overline{M}$ and $\overline{T}$ cannot be found explicitly in terms of model parameters and other states. The general cases are analyzed for stability and, if possible, existence.

Case 1: $\overline{f} = 0$. Mathematically and biologically, this is the simplest case. The only steady-state vector ${\overline{\mathbf{x}}}$ with all nonnegative components for this case is $(\overline{M}, \overline{T}, \overline{E}, \overline{f}) = (0, 0, 0, 0)$. The eigenvalues of the Jacobian matrix (26) evaluated at this state are $-k_3$, $-k_7$, $-k_{10}$, and $k_{11} - k_{12}$, so ${\overline{\mathbf{x}}}$ is stable when $k_{11} < k_{12}$ (when the growth rate of fibroblasts is less than the death rate). This steady state corresponds to a completely unhealed, nonviable tissue condition, with ECM levels at 0. We conclude that the growth rate of fibroblasts must be strictly greater than the decay rate for any healing activity to occur.

Case 2: $\overline{M} = 0, \overline{f} \ne 0$. Solving for the other states gives $\overline{E} = (\overline{f}k_8)/(k_{10}+\overline{f}k_8)$, $\overline{T} = 0$, and the nonzero $\overline{f}$ given in (29). The eigenvalues of (26) evaluated at this state are $-k_3,-k_7$, and the derivatives given in Eqs. (30, 31). Plugging $\overline{f}$ into (31), we see that when $k_{11} > k_{12}$, ${\overline{\mathbf{x}}} = (0,0,\overline{E},\overline{f})$ is a stable steady state. Noting that if $k_{11} < k_{12}$ the nonzero $\overline{f}$ is negative, we conclude that this steady state is stable if it exists. Biologically, this state corresponds to reduced MMP and TIMP activity over time. Wound closure is also closest to 100 % in this case, as $\overline{M} = 0$, making $\overline{E}$ at its maximum in Eq. (28). MMPs are present at low levels except at times of wound healing, so initial activity followed by low concentrations would indicate a healed wound. We conclude that this is the healthiest end state.

Case 3: $\overline{M} \ne 0, \overline{T} = 0,\overline{f} \ne 0$. Rewriting (22) as a polynomial by plugging in $\overline{T}=0$ and multiplying by $(-k_2^3-M^3)/M$,

$$\begin{aligned} \varphi (M)=k_3M^3 - \overline{f}k_1M^2 + k_3k_2^3. \end{aligned}$$

(32)

With this notation, the positive zeros of $\varphi$ are the $\overline{M}$ values of the steady states. It can be checked that $\varphi '(M) = 0$ when $M = 0$ or $2\overline{f}k_1/(3k_3)$. The second root of $\varphi '(M)$ corresponds to the relative minimum of $\varphi (M)$. Since $\varphi (0) > 0$, positive roots exist if and only if the relative minimum is less than or equal to zero.

$$\begin{aligned} 27k_3^2 \cdot \varphi \left( \frac{2\overline{f}k_1}{3k_3}\right) = 27 k_2^3 k_3^3 - 4\overline{f}^3 k_1^3. \end{aligned}$$

(33)

It follows that a steady state exists only if

$$\begin{aligned} 27 k_2^3 k_3^3 \le 4\overline{f}^3 k_1^3. \end{aligned}$$

(34)

To assess the stability of the steady state(s), assume the condition holds. If $\varphi (\overline{M}) = 0$, then by Eq. (32),

$$\begin{aligned} k_2^3+\overline{M}^3 = \frac{k_1\overline{f}\overline{M}^2}{k_3}. \end{aligned}$$

(35)

The eigenvalues of (26) evaluated at $\overline{\mathbf{x}} = (\overline{M},0,\overline{E},\overline{f})$ are the diagonal entries. The entries in the second, third, and fourth rows are negative. Substituting the equality in Eq. (35) and evaluating the eigenvalue $\lambda$ give

$$\begin{aligned} \lambda = k_3 \left( \frac{2\overline{f}k_1-3k_3\overline{M}}{\overline{f}k_1}\right) = \frac{-k_3 \cdot \varphi '(\overline{M})}{\overline{f}k_1\overline{M}}. \end{aligned}$$

(36)

The expression is negative if and only if $\varphi '(\overline{M}) > 0$. It follows that if the condition in Eq. (34) is an equality, then the steady state is unstable. In the case where the condition is a strict inequality, the larger of the two roots is stable.

Case 4: $\overline{M} \ne 0$, $\overline{T} \ne 0$, $\overline{f} \ne 0$ For this case, $\overline{M}$ and $\overline{T}$ cannot be easily found algebraically. Necessary conditions for existence of the nullclines of (22) and (23) in the first quadrant are established to ensure that intersections can occur when $M > 0$ and $T>0$. Solving for T in $p / M=0$ and M in $q / T=0$ gives the nullclines of (22) and (23), respectively,

$$\begin{aligned} T= & {} g(M) = \frac{-k_2^3k_3 + \overline{f}k_1M^2-k_3M^3}{k_4(k_2^3+M^3)} \end{aligned}$$

(37)

$$\begin{aligned} M= & {} h(T) = \frac{k_7(k_6^3+T^3)}{-k_4k_6^3+\overline{f}k_5T^2-k_4T^3}. \end{aligned}$$

(38)

The y-intercept of g(M) is $\frac{-k_3}{k_4}<0$ and $\displaystyle \lim _{M \rightarrow \infty } g(M)=\frac{-k_3}{k_4}<0$. Because g(M) is a continuous function over the interval $[0, \infty )$ the relative maximum in this interval must be greater than 0 for existence in the first quadrant. The only relative maximum value in the domain $[0, \infty )$ is $\frac{2^{2 / 3} \overline{f} k_1-3k_2 k_3}{3k_2 k_4}$. Thus, the condition for the existence of the nullcline (37) in the first quadrant is

$$\begin{aligned} 2^{2 / 3} \overline{f} k_1 > 3k_2 k_3. \end{aligned}$$

(39)

The y-intercept of h(T) is $\frac{-k_7}{k_4}<0$ and $\lim \limits _{T \rightarrow \infty } h(T)=\frac{-k_7}{k_4}<0$. The function is continuous and negative over the domain $T \in [0, \infty )$ unless there is a discontinuity of the second kind resulting from a zero in the denominator. By imposing a condition such that there are exactly two zeros in the denominator in $[0, \infty )$, at least one part of the graph will be in the first quadrant. Let

$$\begin{aligned} \phi (T) = -k_4k_6^3+\overline{f}k_5T^2-k_4T^3. \end{aligned}$$

(40)

Routine computation shows that $\phi '(T) = 0$ when $T = 0$ or $2fk_5 / (3 k_4)$. Noting that $\phi (0) < 0$ and that $\phi$ has positive roots if and only if the relative maximum of $\phi (T)$ is greater than 0,

$$\begin{aligned} 27 k_4^2 \cdot \phi \left( \frac{2\overline{f}k_5}{3k_4}\right) = 4\overline{f}^3k_5^3 - 27 k_4^3 k_6^3. \end{aligned}$$

(41)

It follows that h(T) has discontinuities if and only if

$$\begin{aligned} 4{\overline{f}}^3 k_5^3 > 27 k_4^3 k_6^3. \end{aligned}$$

(42)

Conditions (39) and (42) are necessary conditions for the nullclines’ existence in the first quadrant and are not sufficient conditions for the existence of the steady state(s). To check for stability, we note that the real parts of the eigenvalues of a 2x2 matrix are negative if and only if the trace is negative and determinant is positive. The trace and determinant of matrix (27) are

$$\begin{aligned} {\mathrm {tr}}(J_2)= & {} \frac{k_4M^2g'(M)-k_7Th'(T)}{M}, \end{aligned}$$

(43)

$$\begin{aligned} {\mathrm {det}}(J_2)= & {} k_4k_7(g'(M) \cdot h'(T) + T). \end{aligned}$$

(44)

Setting the trace to be less than 0 and the determinant to be greater than 0, two conditions for stability are found:

$$\begin{aligned}&k_7Th'(T) > k_4M^2g'(M), \end{aligned}$$

(45)

$$\begin{aligned}&g'(M) \cdot h'(T) > -T. \end{aligned}$$

(46)

Both Cases 3 and 4 represent a less complete healing response since long-term MMP activity corresponds to a lower $\overline{E}$ compared to Case 2.