Hydrodynamic model of blood flow in major arteries pulsing in various modes

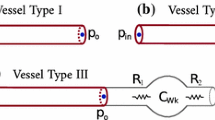
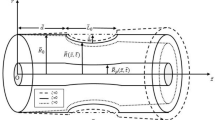
Abstract

Traditionally, the arteries in mammals are viewed as the tubes with elastic wall, whose elasticity could be slowly (during a minute) tuned to change its diameter thereby regulating regional blood supply. Recent findings showed that an artery is a much more sophisticated organ, which can change elasticity of vascular wall within a fraction of a second during a cardiac cycle due to activation of its smooth muscles manifested by generation of arterial action potentials. The rapid variations in elasticity of vascular wall resulted in three basic modes of arterial pulsing: passive, active, and intermediate. The latter is characterized by counteraction of dilation force of arterial pressure and the contractile one of smooth muscle in arterial wall, which can result in seemingly “rigid” artery of constant diameter. The prevalence of any of these forces results in active or passive pulsing modes. Existence of various pulsing modes raises the question of their effect on the main function of blood vessels, i.e., the transport of blood. The aim of this study is to assess the effect of various modes of arterial pulsing on hydraulic impedance of major arteries. The linearized Navier–Stokes equation was employed to develop a model of pulsatile flow of viscous incompressible fluid at small velocity via a conduit artery with the walls of variable or constant elasticity. An essential feature of the developed model is the shape of variable pressure drop applied to the ends of arterial segment, which simulates the real changes in arterial pressure during the heartbeat. Here, it is modeled by periodic (systolic) positive bell-shaped impulses with maxima corresponding to systolic arterial pressure, while the minimal plateau level refers to diastolic arterial pressure. The model assesses the changes in arterial hydraulic impedance during a cardiac cycle relatively to the stable level corresponding to constant blood flow driven by persistent pressure drop. Within intermediate variety of pulsing modes between the active and passive ones, the approximation of rigid arterial segment with infinite elasticity of arterial wall showed that hydraulic impedance in rigid artery is not constant due to inertial properties of the flowing blood. In passive pulsing mode characterized with constant elasticity of arterial wall, the diameter of artery changes in parallel with systolic pressure applied to the ends of arterial segment. At this, the overall change of hydraulic resistance is negative. In active pulsing mode, elasticity of arterial wall varies at different phase shifts relative to arterial pressure due to periodic contractions and relaxation of the smooth muscles in arterial wall. An important feature of active mode is possibility to decrease the hydraulic impedance during the front of arterial pressure. Various experimental modes of artery pulsing can be mathematically simulated. The passive and active modes of pulsing as well as a broad variety of intermediate pulsing modes with various phase shifts between arterial pressure and its diameter result in potency of the arteries to tune its performance in order to meet the regional circulatory requirements. The model showed that active arterial pulsing can diminish the arterial hydraulic impedance and contribute to the work needed for circulation thereby helping the pumping action of the heart.

Graphical abstract