Skip to main content
SpringerLink
Log in

Validation of a clinical finite element model of the human lumbosacral spine

  • Original Article
  • Published:
Medical and Biological Engineering and Computing Aims and scope Submit manuscript

Abstract

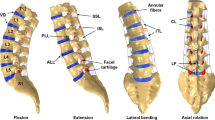
Very few finite element models on the lumbosacral spine have been reported because of its unique biomechanical characteristics. In addition, most of these lumbosacral spine models have been only validated with rotation at single moment values, ignoring the inherent nonlinear nature of the moment–rotation response of the spine. Because a majority of lumbar spine surgeries are performed between L4 and S1 levels, and the confidence in the stress analysis output depends on the model validation, the objective of the present study was to develop a unique finite element model of the lumbosacral junction. The clinically applicable model was validated throughout the entire nonlinear range. It was developed using computed tomography scans, subjected to flexion and extension, and left and right lateral bending loads, and quantitatively validated with cumulative variance analyses. Validation results for each loading mode and for each motion segment (L4-L5, L5-S1) and bisegment (L4-S1) are presented in the paper.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Belytschko T, Kulak R, Schultz A (1974) Finite element stress analysis of an intervetebral disc. J Biomech 7:277–285

    Article  Google Scholar 

  2. Charriere E, Sirey F, Zysset P (2003) A finite element model of the L5–S1 functional spinal unit: development and comparison with biomechanical tests in vitro. Comput Methods Biomech Biomech Eng 6:249–261

    Article  Google Scholar 

  3. Chosa E, Totoribe K, Tajima N (2004) A biomechanical study of lumbar spondylolysis based on a three-dimensional finite element method. J Orthop Res 22:158–163

    Article  Google Scholar 

  4. Decker H, Shapiro S (1957) Herniated lumbar intervertebral disks; results of surgical treatment without the routine use of spinal fusion. AMA Arch Surg 5:77–84

    Google Scholar 

  5. Eberlein R, Holzapfel G, Schulze-Baur C (2001) An anisotropic constitutive model for annulus tissue and enhanced finite element analyses of intact lumbar disc bodies. Comput Meth Biomech Biomed Eng 4:209–230

    Article  Google Scholar 

  6. Eberlein R, Holzapfel G, Frohlich M (2004) Mutli-segment FEA of the human lumbar spine including the heterogeneity of the annulus fibrosus. Comput Mech 4:147–163

    Google Scholar 

  7. Elliott D, Setton L (2000) A linear material model for fiber induced anisotropy of the annulus fibrosus. J Biomech Eng 122:173–179

    Article  Google Scholar 

  8. Elliott D, Setton L (2001) Anisotropic and inhomogenous tensile behavior of the human annulus fibrosus: experimental measurement and material model predictions. J Biomech Eng 123:256–263

    Article  Google Scholar 

  9. Farfan (1973) Mechanical disorder of the low back. Lea & Febiger, Philadelphia

    Google Scholar 

  10. Galante JO (1967) Tensile properties of the human lumbar anulus fibrosus. Acta Orthop Scand Suppl 100:1–91

    Google Scholar 

  11. Goel VK, Goyal S, Clark C, Nishiyama K, Nye T (1985) Kinematics of the whole lumbar spine-effect of discectomy. Spine 10:543–554

    Article  Google Scholar 

  12. Goel VK, Kim YE, Lim TH, Weinstein JN (1988) An analytical investigation of the mechanics of spinal instrumentation. Spine 13:1003–1011

    Article  Google Scholar 

  13. Goel VK, Kong WZ., Han JS, Weinstein JN, Gilbertson LG (1993) A combined finite element and optimization investigation of lumbar spine mechanics with and without muscles. Spine 18:1531–1541

    Article  Google Scholar 

  14. Goel VK, Monroe BT, Gilbertson LG, Brinckmann P (1995) Interlaminar shear stresses and laminae separation in a disc: finite element analysis of the L3–4 motion segment subjected to axial compressive loads. Spine 20:689–698

    Article  Google Scholar 

  15. Klisch S, Lotz J (1999) Application of a fiber-reinforced continuum theory to multiple deformations of the annulus fibrosus. J Biomech 32:1027–1036

    Article  Google Scholar 

  16. Kortelainen P, Puranen J, Koivisto E, Lahde S (1985) Symptoms and signs of sciatica and their relation to the localization of the lumbar disc herniation. Spine 10:88–92

    Article  Google Scholar 

  17. Kulak R, Belytschko T, Schultz A, Galante J (1976) Non-linear behavior of the human intervertebral disc under axial load. J Biomech 9:377–386

    Article  Google Scholar 

  18. Kumaresan S, Yoganandan N, Pintar FA, Maiman DJ, Kuppa S (2000) Biomechanical study of pediatric human cervical spine: a finite element approach. J Biomech Eng 122:60–71

    Article  Google Scholar 

  19. Natarajan R, Andersson G, Patwardhan A, Andriacchi T (1999) Study on effect of graded facetectomy on change in lumbar motion segment torsional flexibility using three-dimensional continuum contact representation for facet joints. J Biomech Eng 121:215–221

    Article  Google Scholar 

  20. Natarajan R, Garretson R, Buyani A, Lim T, Andersson G, Howard A (2003) Effects of slip severity and loading directions on the stability of isthmic spondylolisthesis. Spine 28:1103–1112

    Article  Google Scholar 

  21. Ogden R, Saccomandi G, Sgura I (2004) Fitting hyperelastic models to experimental data. Comput Mech 34:484–502

    Article  MATH  Google Scholar 

  22. Panjabi M, Krag MH, Chung TQ (1984) Effects of disc injury on mechanical behavior of the human spine. Spine 9:707–713

    Article  Google Scholar 

  23. Panjabi M, Yamamoto I, Oxland T, Crisco J (1989) How does posture affect coupling in the lumbar spine? Spine 14:1002–1011

    Article  Google Scholar 

  24. Panjabi M, Oxland T, Yamamoto I, Crisco J (1994) Mechanical behavior of the human lumbar and lumbosacral spine as shown by three-dimensional load-displacement curves. J Bone Joint Surg 76A:413–423

    Google Scholar 

  25. Pintar FA, Yoganandan N, Myers T, Elhagediab A, Sances A Jr (1992) Biomechanical properties of human lumbar spine ligaments. J Biomech 25:1351–1356

    Article  Google Scholar 

  26. Pintar FA, Yoganandan N, Pesigan M, Reinartz JM, Sances A Jr, Cusick JF (1995) Cervical vertebral strain measurements under axial and eccentric loading. J Biomech Eng 117:474–478

    Article  Google Scholar 

  27. Polikeit A, Nolte LP, Ferguson SJ (2003) The effect of cement augmentation on the load transfer in an osteoporotic functional spinal unit: finite-element analysis. Spine 28:991–996

    Article  Google Scholar 

  28. Polikeit A, Nolte LP, Ferguson SJ (2004) Simulated influence of osteoporosis and disc degeneration on the load transfer in a lumbar functional spinal unit. J Biomech 37:1061–1069

    Article  Google Scholar 

  29. Schultz A, Warwick D, Berkson M, Nachemson A (1979) Mechanical behavior of human lumbar spine motion segments—Part I. Responses in flexion, extension, lateral bending and torsion. J Biomech Eng 101:46–52

    Google Scholar 

  30. Sharma M, Langrana NA, Rodriguez J (1995) Role of ligaments and facets in lumbar spinal stability. Spine 20:887–900

    Article  Google Scholar 

  31. Shirazi-Adl SA (1994) Biomechanics of the lumbar spine in sagittal/lateral moments. Spine 19:2407–2414

    Article  Google Scholar 

  32. Shirazi-Adl A, Parnianpour M (1993) Nonlinear response analysis of the human ligamentous lumbar spine in compression. On mechanisms affecting the postural stability. Spine 18:147–158

    Article  Google Scholar 

  33. Shirazi-Adl SA, Shrivastava SC, Ahmed AM (1984) Stress analysis of the lumbar disc-body unit in compression, a three-dimensional nonlinear finite element study. Spine 9:120–134

    Article  Google Scholar 

  34. Shirazi-Adl SA, Ahmed AM, Shrivastava SC (1986) A finite element study of a lumbar motion segment subjected to pure sagittal plane moments. J Biomech 19:331–350

    Article  Google Scholar 

  35. Spangfort E (1972) The lumbar disc herniation. A computer-aided analysis of 2504 operations. Acta Orthop Scand 142:40–44

    Google Scholar 

  36. Tencer A, Ahmed A, Burke D (1982) Some static mechanical properties of the lumbar intervertebral joint, intact and injured. J Biomech Eng 104:193–201

    Google Scholar 

  37. Teo E, Lee K, Ng H, Qiu T, Yang K (2003) Determination of load transmission and contact force at facet joints of L2–3 motion segment using FE method. J Musculoskeltal Res 7:97–109

    Article  Google Scholar 

  38. Teo E, Lee K, Qiu T, Ng H, Yang K (2004) The biomechanics of lumbar graded facetectomy under anterior-shear load. IEEE Trans Biomed Eng 51:443–449

    Article  Google Scholar 

  39. Totoribe K, Tajima N, Chosa E (1999) A biomechanical study of posterolateral lumbar fusion using a three-dimensional nonlinear finite element method. J Orthop Sci 4:115–126

    Article  Google Scholar 

  40. Totoribe K, Chosa E, Tajima N (2004) A biomechanical study of lumbar fusion based on a three-dimensional nonlinear finite element method. J Spinal Dis Tech 17:47–153

    Google Scholar 

  41. Ueno K, Liu YK (1987) A three-dimensional nonlinear finite element model of lumbar intervertebral joint in torsion. Biomech Eng 109:200–209

    Article  Google Scholar 

  42. Wagner D, Lotz J (2004) Theoretical model and experimental results for the nonlinear elastic behavior of human annulus fibrosus. J Orthop Res 22:901–909

    Article  Google Scholar 

  43. Wu HC, Yao RF (1976) Mechanical behavior of the human anulus fibrosus. J Biomech 9:1–7

    Article  Google Scholar 

  44. Yamamoto I, Panjabi M, Crisco T, Oxland T (1989) Three dimensional movements of the whole lumbar spine and lumbosacral joint. Spine 14:1256–1260

    Article  Google Scholar 

  45. Yin L, Elliott D (2004) A homogenization model of the annulus fibrosus. J Biomech 37:907–916

    Article  Google Scholar 

  46. Yoganandan N, Myklebust JB, Ray G, Sances A Jr (1987) Mathematical and finite element analysis of spinal injuries. CRC Rev Biomed Eng 15:29–93

    Google Scholar 

  47. Yoganandan N, Kumaresan S, Voo L, Pintar F (1996) Finite element applications in human cervical spine modeling. Spine 21:1824–1834

    Article  Google Scholar 

  48. Yoganandan N, Kumaresan S, Voo L, Pintar FA (1997) Finite element model of the human lower cervical spine: parametric analysis of the C4–C6 unit. J Biomech Eng 119:87–92

    Article  Google Scholar 

  49. Yoganandan N, Kumaresan S, Pintar FA (2001) Biomechanics of the cervical spine. Part 2. Cervical spine soft tissue responses and biomechanical modeling. Clin Biomech 16:1–27

    Article  Google Scholar 

  50. Zander T, Rohlmanm A, Calisse J, Bergmann G (2001) Estimation of muscle forces in the lumbar spine during upper-body inclination. Clin Biomech 16:S73–S80

    Article  Google Scholar 

  51. Zander T, Rohlmanm A, Bergmann G (2004) Influence of ligament stiffness on the mechanical behavior of a functional spinal unit. J Biomech 37:1107–1111

    Article  Google Scholar 

Download references

Acknowledgments

This study was supported in part by the Department of Veterans Affairs Medical Research.

Author information

Authors and Affiliations

  1. Departments of Neurosurgery, Medical College of Wisconsin, 9200 West Wisconsin Avenue, Milwaukee, WI, 53226, USA

    Yabo Guan, Narayan Yoganandan, Jiangyue Zhang, Frank A. Pintar, Joesph F. Cusick, Christopher E. Wolfla & Dennis J. Maiman

  2. VA Medical Center, Milwaukee, WI, USA

    Yabo Guan, Narayan Yoganandan, Jiangyue Zhang, Frank A. Pintar & Dennis J. Maiman

Authors
  1. Yabo Guan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Narayan Yoganandan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jiangyue Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Frank A. Pintar
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Joesph F. Cusick
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Christopher E. Wolfla
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Dennis J. Maiman
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Narayan Yoganandan.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Guan, Y., Yoganandan, N., Zhang, J. et al. Validation of a clinical finite element model of the human lumbosacral spine. Med Bio Eng Comput 44, 633–641 (2006). https://doi.org/10.1007/s11517-006-0066-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11517-006-0066-9

Keywords

Search

Navigation