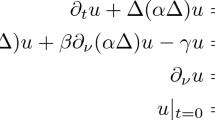Abstract
We study spectral and scattering properties of the Laplacian H (σ)=-Δ in \(L_2(\mathbf{R}^{d+1}_+)\) corresponding to the boundary condition \(\frac{\partial u}{\partial\nu} + \sigma u = 0\) with a periodic function σ. For non-negative σ we prove that H (σ) is unitarily equivalent to the Neumann Laplacian H (0). In general, there appear additional channels of scattering due to surface states. We prove absolute continuity of the spectrum of H (σ) under mild assumptions on σ.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Bibliography
Bentosela, F., Briet, P. and Pastur, L., On the spectral and wave propagation properties of the surface Maryland model, J. Math. Phys. 44 (2003), 1–35.
Birman, M. S., Karadzhov, G. E. and Solomyak, M. Z., Boundedness conditions and spectrum estimates for the operators b(X)a(D) and their analogs, in Estimates and asymptotics for discrete spectra of integral and differential equations, Adv. Soviet. Math. 7, pp. 85–106, Amer. Math. Soc, Providence, RI, 1991.
Birman, M. S. and Suslina, T. A., Periodic magnetic Hamiltonian with variable metric. The problem of absolute continuity, Algebra i Analiz II: 2 (1999), 1–40 (Russian). English transl.: St. Petersbg. Math. J. 11 (2000), 203–232.
Davies, E. B. and Simon, B., Scattering theory for systems with different spatial asymptotics on the left and right, Comm. Math. Phys. 63 (1978), 277–301.
Filonov, N. and Klopp, F., Absolute continuity of the spectrum of a Schrödinger operator with a potential which is periodic in some directions and decays in others, Doc. Math. 9 (2004), 107–121; Erratum: ibid., 135–136.
Filonov, N. and Klopp, F., Absolutely continuous spectrum for the isotropic Maxwell operator with coefficients that are periodic in some directions and decay in others, Comm. Math. Phys. 258 (2005), 75–85.
Frank, R. L., On the scattering theory of the Laplacian with a periodic boundary condition. I. Existence of wave operators, Doc. Math. 8 (2003), 547–565.
Frank, R. L. and Shterenberg, R. G., On the scattering theory of the Laplacian with a periodic boundary condition. II. Additional channels of scattering, Doc. Math. 9 (2004), 57–77.
Grossmann, A., Hoegh-Krohn, R. and Mebkhout, M., The one particletheory of periodic point interactions. Polymers, mono-molecular layers, and crystals, Comm. Math. Phys. 77 (1980), 87–110.
Jakšić, V., Spectral Theory of Corrugated Surfaces, in Journées “Équations aux Dérivées Partielles” (Plestin-les-Grèves, 2001), Exp. No. VIII, Univ. Nantes, Nantes, 2001.
Karpeshina, Y. E., Spectrum and eigenfunctions of Schrödinger operator with the zero-range potential of the homogeneous two-dimensional lattice type in three-dimensional space, Theoret. and Math. Phys. 57 (1983), 1231–1237.
Kato, T., Perturbation Theory for Linear Operators, Springer, Berlin–New York 1976.
Lions, J. L. and Magenes, E., Non-Homogeneous Boundary Value Problems and Applications. I, Springer, New York–Heidelberg 1972.
Sáenz, A. W., Quantum-mechanical scattering by impenetrable periodic surfaces, J. Math. Phys. 22 (1981), 2872–2884.
Thomas, L., Time dependent approach to scattering from impurities in a crystal, Comm. Math. Phys. 33 (1973), 335–343.
Wloka, J., Partial Differential Equations, Cambridge University Press, Cambridge, 1987.
Yafaev, D. R., Mathematical Scattering Theory, Amer. Math. Soc., Providence, RI, 1992.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Frank, R. On the Laplacian in the halfspace with a periodic boundary condition. Ark Mat 44, 277–298 (2006). https://doi.org/10.1007/s11512-005-0012-3
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11512-005-0012-3