Introduction

Solid-state electromagnetic (EM) resonators are one of the key elements in microwave and optoelectronic applications. They are used as frequency stabilizers [1], filters [2], biosensors [3,4,5], and solar cell components [6,7,8], and can also be applicable in medicine [9] and precise material measurement systems [10]. One of the most important parameters of a solid-state resonator (SSR) is a Q-factor, which is the ratio of stored EM energy to the power dissipated per cycle. For unshielded resonators, dissipated power depends not only on dielectric and magnetic medium losses but also on radiation losses. Some SSRs exhibit Q-factors as large as 10 [9] at microwave [10] or optical frequencies [11]. Others, like spherical yttrium-iron-garnet (YIG) resonators, can be tuned with a static magnetic field bias (SMFB) in a broad microwave frequency range [2]. There are two distinct classes of resonances in SSRs: ordinary EM resonances occurring in non-dispersive low-loss media of given shape or plasmon resonances (PRs) occurring in samples made of dielectric (magnetic) medium exhibiting negative permittivity (permeability). For the ordinary EM resonances, the average electric and magnetic energy stored in the resonator per oscillation cycle are equal to each other at a resonance frequency. On the contrary, such equality does not take place in case of electric (magnetic) PRs, where the average electric (magnetic) energy stored in the resonator per cycle is hundreds of times larger than the average magnetic (electric) energy. That property has recently been proven for the magnetic PRs (MPRs) [12]. Formally, the analysis of free oscillations of the EM resonance system can be formulated as an eigenvalue problem for Maxwell equations. Rigorous solutions of Maxwell equations are available for spherical and cylindrical resonators containing isotropic media [13], while for the resonator having other shapes numerical solutions can be usually obtained with sufficient accuracy. PRs have been often analyzed employing either electro- or magneto-static approximation. Such approach allows to determine PR frequencies of small spherical particles having diameter d << λ, where λ is the free-space wavelength. The use of the quasi-static approach to the analysis of the electric PRs has been known for over 100 years and it is described in textbooks on plasmonics [14, 15]. It should be only mentioned that according to the quasi-static approximation the dominant electric PR (a so-called electric dipole mode) in a spherical sample located in the free space occurs when dielectric constant of the sphere is equal to εr′ = − 2. What can also be distinguished are magneto-static spin modes, which are often related in the literature to free oscillations of gyromagnetic spheroids. Magnetostatic theory of these modes was developed by Walker [16] and Fletcher [17]. The dominant mode occurring in the gyromagnetic sphere is referred in the literature as the mode of uniform precession, which occurs when scalar permeability of the clockwise circularly polarized (CCP) EM field in an infinitesimally small sample is equal to μr = − 2. Although this condition has been known for decades, only recently [12, 18], it has been shown that the mode of uniform precession is in fact the fundamental MPR occurring in the gyromagnetic sphere. Unfortunately, the quasi-static theory does not allow to determine the Q-factor of a plasmonic resonator and, in addition, the theory fails for larger samples. Despite obvious similarities, the modes of uniform precession occurring in gyromagnetic resonators have usually been considered as a different class of problems than dielectric plasmons. In the view of the above, the main goal of this paper is to present a general study of the Q-factor of the family of electric and magnetic PRs as well as whispering gallery mode (WGM) dielectric resonators, employing unified electrodynamic theory in order to show how the Q-factor is limited by medium and radiation losses. In addition, the impact of the finite size of the resonator on the resonance frequency and Q-factor is considered.

Electrodynamic Analysis

It is well known that complex permittivity of gaseous plasma and metals exhibits negative values at a certain range of frequencies, which depends on the angular plasma frequency, ωp, according to the Drude model [19]:

$$ {\varepsilon}_r={\varepsilon_r}^{\prime }-j{\varepsilon_r}^{\prime \prime }={\varepsilon}_{\infty }-\frac{\omega_p^2}{{\widehat{\omega}}^2-j\widehat{\omega}\Gamma} $$
(1)

where ε∞ is the permittivity at infinite frequency (usually in the range 1–10) and Γ is a damping factor. Plasma frequency depends on the square root of the density of the free charge carriers and it can vary from MHz range for atmospheric plasma to optical frequencies for noble metals. The dominant electric PR appears also in an infinitesimally small dielectric sphere located in the free space at a frequency corresponding to the εr′ =  − 2 condition.

For ferrimagnetic materials, such as microwave ferrites and garnets biased with the internal SMFB H0, permeability becomes a Polder’s tensor with a diagonal component μ and an off-diagonal component κ occurring in the plane orthogonal to the internal SMFB H0. If CCP high-frequency (HF) magnetic field is orthogonal to H0, magnetic properties of ferromagnetic medium can be characterized by the following effective complex scalar permeability [20]:

$$ {\mu}_r=\mu +\kappa ={\mu_r}^{\prime }-j{\mu_r}^{\prime \prime }=1+\frac{H_{0r}+\widehat{w}+j\ \alpha\ \widehat{w}}{H_{0r}^2-{\widehat{w}}^2+2\ j\ \alpha\ {H}_{0r}\ \widehat{w}} $$
(2)

where H0r = H0/MS , \( \widehat{w}=\widehat{f}/{f}_m \), fm = γMS, MS is the saturation magnetization of ferrimagnetic medium, γ = 35.19 MHz/(kA/m), α is the Gilbert damping factor, and \( \widehat{f} \) is the complex frequency. In the description of ferromagnetic materials, the Gilbert damping factor α is often exchanged with the ferromagnetic linewidth ∆H = 2αH0, as alternative measure of losses. In case of spherical YIG samples, the internal SMFB H0 is related to the external bias He by the formula \( {H}_0={H}_e-\frac{{\mathrm{M}}_{\mathrm{S}}}{3}-\delta {H}_a \), where δHa is the effective anisotropy field, which depends on the orientation of the ferrimagnetic crystal with respect to H0. For a specific orientation (δHa = 0), the relationship between the normalized internal and external static magnetic fields is \( {H}_{0r}={H}_{er}-\frac{1}{3} \), where Her = He/MS. For lossless gyromagnetic medium, Eq. (2) can be simplified as follows:

$$ {\mu}_r=1+\frac{1}{H_{0r}-w\ } $$
(3)

As it can be noticed, ferromagnetic resonance occurs at wFMR = H0r. However, recent studies [18] of YIG filters and oscillators revealed that the dominant MPR mode excited in the infinitesimally small ferromagnetic sphere occurs when μr′ =  − 2, which leads to the following condition \( {w}_{MPR}={H}_{0r}+\frac{1}{3} \). The normalized internal SMFB, H0r, can be replaced with the external one, Her, leading to the following condition wMPR = Her.

Time dependence of the solution of the eigenvalue problem for free oscillations of a resonance system can be expressed in the form of complex eigenfrequencies, \( {\widehat{\omega}}_s={\omega}_s^{\prime }+j{\omega}_s^{\prime \prime } \), corresponding to specific modes with the Q-factors that, by definition, can be evaluated as\( {Q}_s=\frac{\omega_s^{\prime }}{2{\omega}_s^{\prime \prime }} \). Rigorous solutions of Maxwell equations, that describe free oscillations of SSRs, are known for isotropic spheres situated in isotropic medium (see Fig. 1).

Fig. 1
figure 1

a Dielectric and b ferrimagnetic sphere in dielectric medium

Full size image

Resonance condition for the TMn0p modes (subscripts indicate the mode orders along ϴ φ r spherical coordinates) of free oscillations of an isotropic sphere having permittivity εr, as given by Eq. (1), immersed in dielectric medium having permittivity εd can be formulated in the following form [12]:

$$ {\varepsilon}_d\left\{n{J}_{n+\frac{1}{2}}\left(k{R}_1\right)-k{J}_{n-\frac{1}{2}}\left(k{R}_1\right)\right\}{H}_{n+\frac{1}{2}}^{(2)}\left({k}_0{R}_1\right)-{\varepsilon}_r\left\{n{H}_{n+\frac{1}{2}}^{(2)}\left({k}_0{R}_1\right)-{k}_0{H}_{n-\frac{1}{2}}^{(2)}\left({k}_0{R}_1\right)\right\}{J}_{n+\frac{1}{2}}\left(k{R}_1\right)=0 $$
(4)

where \( k=\widehat{\omega}/c{\left({\varepsilon}_r\right)}^{0.5} \), \( {k}_0=\widehat{\omega}/c{\left({\varepsilon}_d\right)}^{0.5} \), εr is the relative complex permittivity of the sphere, εd is the relative complex permittivity of medium surrounding the sphere, n and p are elevation and radial mode indices, respectively, c is the speed of the EM wave in vacuum, and J (H) is a Bessel (Hankel) function.

Similarly, resonance condition for the TEn0p modes of free oscillations of the isotropic sphere having permeability μr, as defined in Eq. (2), relative complex permittivity εf, and immersed in dielectric medium having permittivity εd can be formulated in the following form:

$$ \left\{n{J}_{n+\frac{1}{2}}\left(k{R}_1\right)-k{J}_{n-\frac{1}{2}}\left(k{R}_1\right)\right\}{H}_{n+\frac{1}{2}}^{(2)}\left({k}_0{R}_1\right)-{\mu}_r\left\{n{H}_{n+\frac{1}{2}}^{(2)}\left({k}_0{R}_1\right)-{k}_0{H}_{n-\frac{1}{2}}^{(2)}\left({k}_0{R}_1\right)\right\}{J}_{n+\frac{1}{2}}\left(k{R}_1\right)=0 $$
(5)

The radial mode index p denotes subsequent roots of Eq. (4) or (5), while the azimuthal mode index m has no impact on the resonance frequency, so it is assumed to be m = 0. Transcendental equations are also available for more complicated multilayered dielectric structures having spherical symmetry [13]. It will be shown that basic properties of the electric plasmon resonance and TMn0p WGMs can be analyzed employing the solution of Eq. (4), while basic properties of MPR and TEn0p WGMs can be analyzed employing Eq. (5).

Experimental Setup

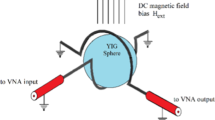
Measurements of the resonance frequencies and Q-factors of MPRs have been performed employing Agilent Technologies’ PNA-X vector network analyzer (VNA). Experimental setup is shown in Fig. 2. A gyromagnetic YIG sphere was mounted on the top of a thin fused silica rod and it was coupled to VNA ports with two orthogonal semi-loops. The experimental setup with the YIG sample was placed between the magnet poles from Bruker EPR spectrometer. For fixed positions of the coupling semi-loops the coupling coefficients vary when resonator is tuned with the DC magnetic field. The loaded Q-factor (Q-factor including coupling losses) of the YIG resonator was measured directly with VNA and, subsequently, the unloaded Q-factor was determined by measuring three components of the scattering matrix, namely, S11, S22, and S21 at a certain frequency range in the vicinity of the resonance frequency [20].

Fig. 2
figure 2

Top and side view of the setup for the measurement of the resonance frequency and Q-factor as a function of the static magnetic field bias in gyromagnetic spheres

Full size image

Results of Computations and Experiments

Electric PRs have been analyzed by solving Eq. (4) assuming that permittivity of plasmonic spheres is defined in Eq. (1) and the spheres are situated in vacuum (εd = 1). Equation 4 is nonlinear with respect to \( \widehat{\omega} \) and, as such, it can be solved with either Levenberg-Marquardt or Newton method. Computations have been performed for various diameters of the plasmonic sphere and for fixed parameters of the permittivity model (ε∞ = 1) and the starting point for the root finding of Eq. (4) was assumed as \( \widehat{\omega}={\omega}_p/\sqrt{3} \). Figure 3a shows the obtained relation between the normalized diameter of the plasmonic sphere and the resonance frequency as compared to the quasi-static approximation of the resonance frequency f0 of an infinitesimally small sphere. For the infinitesimally small sample, the resonance frequency is approaching \( \mathit{\operatorname{Re}}\left(\widehat{\omega}\right)={\omega}_p/\sqrt{3} \), which corresponds to εr′ =  − 2. For larger samples, the resonance frequency is getting smaller than \( {\omega}_p/\sqrt{3} \) and, consequently, the corresponding permittivity decreases as well. The results shown in Fig. 3a are known as the red-shift phenomenon when the size of metal particles becomes larger. Figure 3b shows the relation between the size of the sample and the Q-factor computed for a few values of the damping factor Γ. Results for Γ = 0 represent the Q-factor due to radiation losses only, which behaves as \( {\mathrm{Q}}_r\propto {\left(\frac{d}{\lambda}\right)}^{-3} \) (see an analytical fitting function given in the inset in Fig. 3b). Additional curves plotted in Fig. 3b were calculated assuming the damping factor of gold (red curve) and silver (blue curve). Parameters of a Drude model for various metals that can be used for more accurate computations can be found in the literature [21]. As it is seen in Fig. 3b, radiation losses are dominant for large metal particles (d/λ > 0.05), so it is necessary to make them sufficiently small to obtain a larger Q-factor of the plasmonic mode. Despite a moderate level of the Q-factor achievable with the electric PRs, they have found applications in sensors, photothermal cancer therapy [9], and solar cells [6,7,8].

Fig. 3
figure 3

(a) Dielectric constant (left scale) and the corresponding resonance frequency normalized to the resonance frequency obtained for the infinitesimally small plasmonic sphere (right scale) at the electric PR found with Eq. (4) versus normalized diameter of the dielectric sphere, and (b) Q-factor due to dielectric and radiation losses versus normalized diameter of the dielectric sphere. Black dashed line denotes a fitting function for Γ = 0 (radiation losses only)

Full size image

Subsequently, let us consider MPRs, which have been employed in YIG microwave filters and oscillators for decades, although their physical nature has been described only recently [12, 18]. Optical MPRs have been, so far, unknown [22]. The analysis of MPRs based on the solution of Eq. (5) for permeability given in Eq. (3) is presented in Fig. 4, which shows deviation of the normalized frequency w from the quasi-static limit (\( {w}_{MPR}={H}_{0r}+\frac{1}{3} \)) and the corresponding Q-factor versus normalized diameter of the YIG sphere.

Fig. 4
figure 4

(a) MPR condition (left scale) and the corresponding effective permeability (right scale) versus normalized diameter of a YIG sphere having MS = 140 kA/m. (b) Q-factor due to magnetic (solid lines) and radiation losses (dashed lines) evaluated for MS = 140 kA/m, ∆H = 0.5 Oe and 3 different diameters of YIG spheres

Full size image

In contrast to electric PRs discussed earlier, computations and measurements were performed for variable frequency as YIG resonators are tuneable. However, it can be noticed that the resonance condition varies with d/λ in a qualitatively similar manner for the electric (see Fig. 3a) and magnetic (see Fig. 4a) PRs. Figure 4 shows the results of Q-factor computations with Eq. (5) versus normalized diameter of the ferromagnetic sphere. Additionally, experiments for the YIG sphere having d = 0.5 mm and ∆H = 0.5 Oe are presented, which are in good agreement with computations (see blue curve in Fig. 4b). If magnetic losses are neglected, as in Eq. (3), the Q-factor due to radiation losses can be approximated by the expression: \( {\mathrm{Q}}_r\propto {\left(\frac{d}{\lambda}\right)}^{-2} \) (see dashed lines in Fig. 4b). This is different than for the electric PR (compare the inset in Fig. 3b) due to the fact that the results presented in Fig. 4b are obtained for variable frequency. If the frequency was kept constant, Qr would have exactly the same dependence as for the electric PR. It should be also mentioned that contrary to the damping factor Γ in the electric PR, experiments show that the Gilbert damping factor in Eq. (2) varies with frequency for a given YIG sphere, while the ferromagnetic linewidth ∆H is frequency independent [12]. As a result, the Q-factor due to magnetic losses, Qm = H0r/∆H, increases linearly with frequency (see black dashed line in Fig. 4b). Eventually, the total Q-factor of the unshielded YIG resonator typically approaches maximum at some frequency, when Qm = Qr, which is confirmed theoretically and experimentally, as shown in Fig. 4b. Theoretically, smaller samples can achieve a larger Q-factor; however, in practice, this is limited by the imperfect quality of their surface [23], which should be optically polished to get the highest Q-factor. The smallest diameter of commercially available YIG resonators is about d = 0.25 mm with ∆H~ 0.3 Oe, which leads to the Q-factor of the unshielded YIG resonator as large as 10 [4].

WGMs are another interesting class of resonances in spherical samples that can be solved with the transcendental equations given in Eqs. (4) and (5). These modes can be of either TMnnp or TEnnp type and can exhibit record low radiation losses (large Qr) in low-loss non-dispersive dielectric samples from microwave to optical frequencies. Figure 5a presents normalized frequency of a TEn01 WGM as a function of dielectric constant. It is seen that frequency separation between the subsequent modes become similar for larger n. For large dielectric constant, the normalized frequency practically does not depend on permittivity, which is related to the fact that vast majority of EM energy is concentrated inside the sphere and distributed around its circumference. Figure 5b shows the Q-factor due to radiation losses computed as a function of the elevation mode index n.

Fig. 5
figure 5

(a) Normalized frequency of the TEn01 WGM versus dielectric constant in spherical samples. (b) Q-factor due to radiation losses versus the elevation angle mode index n of the TEn01 WGM

Full size image

The Q-factor due to radiation losses of WGM resonators made of low-loss dielectrics having εr′ ≥ 10, which is common for several materials at microwave frequencies, can be as high as Qr > 108 for the elevation mode index n > 12. In that case, the total unloaded Q-factor Qu predominantly depends on dielectric losses provided that tanδ > 10−8, so that dielectric losses are larger than radiation losses (Qd < Qr). This is the reason for using WGM resonators for the most sensitive and the most accurate measurements of the complex permittivity at microwave frequencies [10]. At optical frequencies, most dielectrics have small permittivity (e.g., εr′ ≈ 2.125 for fused silica [24, 25], εr′ ≈ 5.84 for diamond, and εr′ ≈ 4.66 for cubic zirconia [26]) and their dielectric loss tangent is at the order of 10−9 at room temperatures, which is 4 orders of magnitude less than at microwave frequencies. Consequently, as it is seen in Fig. 5b, radiation losses are no longer negligible. For instance, in fused silica sphere, situated in free space, the elevation mode index should be n > 60 to obtain Qr ≈ 108. Nevertheless, fused silica WGM resonators having Q-factor at the order of 109 have been reported, which means that they had to operate on the mode with the elevation mode index of ca. 70. As it is seen in Fig. 5b, WGM resonators made of higher permittivity materials, such as cubic zirconia or diamond, would allow operation at lower elevation order modes than for fused silica WGM resonators, maintaining large Qr.

Conclusions

It has been shown that basic properties of spherical PRs but also WGM resonators, operating from microwaves to optical frequencies, can be rigorously determined employing unified electrodynamic analysis. For PRs, the Q-factor due to radiation losses varies at a given frequency as \( {\mathrm{Q}}_r\propto {\left(\frac{d}{\lambda}\right)}^{-3} \). In practice, the Q-factor is limited in WGM resonators by dielectric losses, provided that the mode order is large enough to make sure that Qd < Qr. Similar properties can be observed in electric PRs where the Q-factor is limited by the imaginary part of permittivity. In case of magnetic PRs, like YIG sphere, three kinds of losses have comparable influence on the Q-factor: magnetic intrinsic losses are dominant at lower frequencies, radiation losses limit the Q-factor at higher frequencies, and surface roughness limits the Q-factor especially for very small samples.