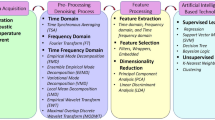
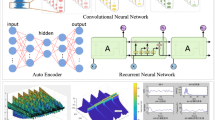
Abstract
Machinery fault diagnosis has progressed over the past decades with the evolution of machineries in terms of complexity and scale. High-value machineries require condition monitoring and fault diagnosis to guarantee their designed functions and performance throughout their lifetime. Research on machinery Fault diagnostics has grown rapidly in recent years. This paper attempts to summarize and review the recent R&D trends in the basic research field of machinery fault diagnosis in terms of four main aspects: Fault mechanism, sensor technique and signal acquisition, signal processing, and intelligent diagnostics. The review discusses the special contributions of Chinese scholars to machinery fault diagnostics. On the basis of the review of basic theory of machinery fault diagnosis and its practical applications in engineering, the paper concludes with a brief discussion on the future trends and challenges in machinery fault diagnosis.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Roy R, Stark R, Tracht K, et al. Continuous maintenance and the future—Foundations and technological challenges. CIRP Annals-Manufacturing Technology, 2016, 65(2): 667–688
Yan R, Gao R X. Wavelet transform: A mathematical tool for nonstationary signal processing in measurement science Part 2 in a series of tutorials in instrumentation and measurement. IEEE Instrumentation & Measurement Magazine, 2009, 12(5): 35–44
Lewicki D G, Decker H J, Shimski J T. Development of a full-scale transmission testing procedure to evaluate advanced lubricants. NASA Technical Report 92N30396. 1992
Samuel P D, Pines D J. A review of vibration-based techniques for helicopter transmission diagnostics. Journal of Sound and Vibration, 2005, 282(1–2): 475–508
Chen B, Zhang Z, Zi Y, et al. Detecting of transient vibration signatures using an improved fast spatial-spectral ensemble kurtosis kurtogram and its applications to mechanical signature analysis of short duration data from rotating machinery. Mechanical Systems and Signal Processing, 2013, 40(1): 1–37
Cai G, Chen X, He Z. Sparsity-enabled signal decomposition using tunable Q-factor wavelet transform for fault feature extraction of gearbox. Mechanical Systems and Signal Processing, 2013, 41(1–2): 34–53
McGarry B. Pratt & Whitney: F-35 fleet will have engine fix by early 2016. 2015. Retrieved form http://www.dodbuzz.com/2015/06/15/pratt-whitney-f-35-fleet-will-have-engine-fix-by-early-2016/
Clark C. JSF fire looks like ‘Isolated Event’; F-35A stay on ground. 2014. Retrieved form http://breakingdefense.com/2014/06/jsf-fire-looks-like-isolated-event-f-35bs-should-fly-tomorrow/
Clark C. F-35 head bogdan explains the F135 ‘Bad Rub’ Fix. 2014. Retrieved form http://breakingdefense.com/2014/09/cost-for-f135-bad-rub-fix-should-be-low-mg-bogdan/
Devendiran S, Manivannan K. Vibration based condition monitoring and fault diagnosis technologies for bearing and gear components—A review. International Journal of Applied Engineering Research, 2016, 11(6): 3966–3975
Desbazeille M, Randall R B, Guillet F, et al. Model-based diagnosis of large diesel engines based on angular speed variations of the crankshaft. Mechanical Systems and Signal Processing, 2010, 24(5): 1529–1541
Gupta P. Dynamics of rolling-element bearings—Part I: Cylindrical roller bearing analysis. Journal of Lubrication Technology, 1979, 101(3): 293–302
Gupta P K. Dynamics of rolling-element bearings. 1. Cylindrical roller bearing analysis. Journal of lubrication technology, 1979, 101: 293–304
Gupta P K. Dynamics of rolling-element bearings. 2. Cylindrical roller bearing results. Journal of lubrication technology, 1979, 101: 305–311
Gupta P K. Dynamics of rolling-element bearings. 3. Ball bearing analysis. Journal of lubrication technology, 1979, 101: 312–318
Gupta P K. Dynamics of rolling-element bearings. 4. Ball bearing results. Journal of lubrication technology, 1979, 101: 319–326
Gupta P K. Advanced Dynamics of Rolling Elements. New York: Springer, 1984
Niu L, Cao H, He Z, et al. Dynamic modeling and vibration response simulation for high speed rolling ball bearings with localized surface defects in raceways. Journal of Manufacturing Science and Engineering, 2014, 136(4): 041015
Wang F, Jing M, Yi J, et al. Dynamic modelling for vibration analysis of a cylindrical roller bearing due to localized defects on raceways. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics, 2015, 229(1): 39–64
Moazen Ahmadi A, Petersen D, Howard C. A nonlinear dynamic vibration model of defective bearings—The importance of modelling the finite size of rolling elements. Mechanical Systems and Signal Processing, 2015, 52–53: 309–326
Niu L, Cao H, He Z, et al. A systematic study of ball passing frequencies based on dynamic modeling of rolling ball bearings with localized surface defects. Journal of Sound and Vibration, 2015, 357: 207–232
Patel V, Tandon N, Pandey R. A dynamic model for vibration studies of deep groove ball bearings considering single and multiple defects in races. Journal of Tribology, 2010, 132(4): 041101
Ma H, Pang X, Feng R, et al. Fault features analysis of cracked gear considering the effects of the extended tooth contact. Engineering Failure Analysis, 2015, 48: 105–120
Ma H, Song R, Pang X, et al. Time-varying mesh stiffness calculation of cracked spur gears. Engineering Failure Analysis, 2014, 44: 179–194
Dimarogonas A D. Vibration of cracked structures: A state of the art review. Engineering Fracture Mechanics, 1996, 55(5): 831–857
Wauer J. On the dynamics of cracked rotors: A literature survey. Applied Mechanics Reviews, 1990, 43(1): 13–17
Gasch R. A survey of the dynamic behaviour of a simple rotating shaft with a transverse crack. Journal of Sound and Vibration, 1993, 160(2): 313–332
Bachschmid N, Pennacchi P. Crack effects in rotor dynamics. Mechanical Systems and Signal Processing, 2008, 22(4): 761–762
Pennacchi P, Bachschmid N, Vania A. A model-based identification method of transverse cracks in rotating shafts suitable for industrial machines. Mechanical Systems and Signal Processing, 2006, 20(8): 2112–2147
Papadopoulos C A. The strain energy release approach for modeling cracks in rotors: A state of the art review. Mechanical Systems and Signal Processing, 2008, 22(4): 763–789
Sekhar A. Multiple cracks effects and identification. Mechanical Systems and Signal Processing, 2008, 22(4): 845–878
Gasch R. Dynamic behaviour of the Laval rotor with a transverse crack. Mechanical Systems and Signal Processing, 2008, 22(4): 790–804
Pennacchi P, Bachschmid N, Vania A, et al. Use of modal representation for the supporting structure in model-based fault identification of large rotating machinery: Part 1—Theoretical remarks. Mechanical Systems and Signal Processing, 2006, 20(3): 662–681
Pennacchi P, Vania A, Bachschmid N. Increasing the robustness of fault identification in rotor dynamics by means of M-estimators. Mechanical Systems and Signal Processing, 2007, 21(8): 3003–3029
Simani S, Fantuzzi C. Dynamic system identification and modelbased fault diagnosis of an industrial gas turbine prototype. Mechatronics, 2006, 16(6): 341–363
Simani S, Patton R J. Fault diagnosis of an industrial gas turbine prototype using a system identification approach. Control Engineering Practice, 2008, 16(7): 769–786
Hou L, Chen Y, Cao Q, et al. Nonlinear vibration analysis of a cracked rotor-ball bearing system during flight maneuvers. Mechanism and Machine Theory, 2016, 105: 515–528
Lu K, Jin Y, Chen Y, et al. Stability analysis of reduced rotor pedestal looseness fault model. Nonlinear Dynamics, 2015, 82(4): 1611–1622
Liang X, Zuo M J, Hoseini M R. Vibration signal modeling of a planetary gear set for tooth crack detection. Engineering Failure Analysis, 2015, 48: 185–200
Ma H, Tai X, Han Q, et al. A revised model for rubbing between rotating blade and elastic casing. Journal of Sound and Vibration, 2015, 337: 301–320
Ma H, Zeng J, Feng R, et al. Review on dynamics of cracked gear systems. Engineering Failure Analysis, 2015, 55: 224–245
Ma H, Lu Y, Wu Z, et al. Vibration response analysis of a rotational shaft-disk-blade system with blade-tip rubbing. International Journal of Mechanical Sciences, 2016, 107: 110–125
Ma H, Pang X, Zeng J, et al. Effects of gear crack propagation paths on vibration responses of the perforated gear system. Mechanical Systems and Signal Processing, 2015, 62–63: 113–128
Hu Z, Tang J, Zhong J, et al. Frequency spectrum and vibration analysis of high speed gear-rotor system with tooth root crack considering transmission error excitation. Engineering Failure Analysis, 2016, 60: 405–441
Gui Y, Han Q, Chu F. A vibration model for fault diagnosis of planetary gearboxes with localized planet bearing defects. Journal of Mechanical Science and Technology, 2016, 30(9): 4109–4119
Tadina M, Boltežar M. Improved model of a ball bearing for the simulation of vibration signals due to faults during run-up. Journal of Sound and Vibration, 2011, 330(17): 4287–4301
Geng Z, Chen J, Barry Hull J. Analysis of engine vibration and design of an applicable diagnosing approach. International Journal of Mechanical Sciences, 2003, 45(8): 1391–1410
Wang H, Chen P. Fault diagnosis for a rolling bearing used in a reciprocating machine by adaptive filtering technique and fuzzy neural network. WSEAS Transactions on Systems, 2008, 7(1): 1–6
Wang H, Chen P. A feature extraction method based on information theory for fault diagnosis of reciprocating machinery. Sensors (Basel), 2009, 9(4): 2415–2436
Lee S, White P. The enhancement of impulsive noise and vibration signals for fault detection in rotating and reciprocating machinery. Journal of Sound and Vibration, 1998, 217(3): 485–505
Shen L, Tay F E, Qu L, et al. Fault diagnosis using rough sets theory. Computers in Industry, 2000, 43(1): 61–72
Wang J, Hu H. Vibration-based fault diagnosis of pump using fuzzy technique. Measurement, 2006, 39(2): 176–185
El-Ghamry M, Reuben R, Steel J. The development of automated pattern recognition and statistical feature isolation techniques for the diagnosis of reciprocating machinery faults using acoustic emission. Mechanical Systems and Signal Processing, 2003, 17(4): 805–823
Östman F, Toivonen H T. Active torsional vibration control of reciprocating engines. Control Engineering Practice, 2008, 16(1): 78–88
Schultheis S M, Lickteig C A, Parchewsky R. Reciprocating compressor condition monitoring. In: Proceedings of 36th Turbomachinery Symposium. College Station, 2000, 10–13
Goodwin M, Nikolajsen J, Ogrodnik P. Reciprocating machinery bearing analysis: Theory and practice. Proceedings of the Institution of Mechanical Engineers. Part J: Journal of Engineering Tribology, 2003, 217(6): 409–426
Pituba J J C, Fernandes G R, de Souza Neto E A. Modeling of cohesive fracture and plasticity processes in composite microstructures. Journal of Engineering Mechanics, 2016, 142(10): 04016069
Zuo H, Yang Z, Chen X, et al. Analysis of laminated composite plates using wavelet finite element method and higher-order plate theory. Composite Structures, 2015, 131: 248–258
Cavalcante M A, Khatam H, Pindera M J. Homogenization of elastic-plastic periodic materials by FVDAM and FEM approaches— An assessment. Composites Part B: Engineering, 2011, 42 (6): 1713–1730
Pindera M J, Khatam H, Drago A S, et al. Micromechanics of spatially uniform heterogeneous media: A critical review and emerging approaches. Composites Part B: Engineering, 2009, 40 (5): 349–378
Cavalcante M A, Pindera M J, Khatam H. Finite-volume micromechanics of periodic materials: Past, present and future. Composites Part B: Engineering, 2012, 43(6): 2521–2543
Tu W, Pindera M J. Cohesive zone-based damage evolution in periodic materials via finite-volume homogenization. Journal of Applied Mechanics, 2014, 81(10): 101005
Chen Q, Chen X, Zhai Z, et al. Micromechanical modeling of viscoplastic behavior of laminated polymer composites with thermal residual stress effect. Journal of Engineering Materials and Technology, 2016, 138(3): 031005
Chen Q, Chen X, Zhai Z, et al. A new and general formulation of three-dimensional finite-volume micromechanics for particulate reinforced composites with viscoplastic phases. Composites Part B: Engineering, 2016, 85: 216–232
Joosse P, Blanch M, Dutton A, et al. Acoustic emission monitoring of small wind turbine blades. Journal of Solar Energy Engineering, 2002, 124(4): 446–454
Schroeder K, Ecke W, Apitz J, et al. A fibre Bragg grating sensor system monitors operational load in a wind turbine rotor blade. Measurement Science & Technology, 2006, 17(5): 1167–1172
Tian S, Yang Z, Chen X, et al. Damage detection based on static strain responses using FBG in a wind turbine blade. Sensors (Basel), 2015, 15(8): 19992–20005
Mitra M, Gopalakrishnan S. Guided wave based structural health monitoring: A review. Smart Materials and Structures, 2016, 25(5): 053001
Raghavan A, Cesnik C E. Review of guided-wave structural health monitoring. Shock and Vibration Digest, 2007, 39(2): 91–114
Park H W, Kim S B, Sohn H. Understanding a time reversal process in Lamb wave propagation. Wave Motion, 2009, 46(7): 451–467
Park HW, Sohn H, Law K H, et al. Time reversal active sensing for health monitoring of a composite plate. Journal of Sound and Vibration, 2007, 302(1–2): 50–66
Lin J, Gao F, Luo Z, et al. High-resolution Lamb wave inspection in viscoelastic composite laminates. IEEE Transactions on Industrial Electronics, 2016, 63(11): 6989–6998
Lin J, Hua J, Zeng L, et al. Excitation waveform design for lamb wave pulse compression. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2016, 63(1): 165–177
Hall J S, Michaels J E. Minimum variance ultrasonic imaging applied to an in situ sparse guided wave array. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2010, 57 (10): 2311–2323
Hall J S, McKeon P, Satyanarayan L, et al. Minimum variance guided wave imaging in a quasi-isotropic composite plate. Smart Materials and Structures, 2011, 20(2): 025013
Levine R M, Michaels J E. Model-based imaging of damage with Lamb waves via sparse reconstruction. Journal of the Acoustical Society of America, 2013, 133(3): 1525–1534
Li X, Yang Z, Zhang H, et al. Crack growth sparse pursuit for wind turbine blade. Smart Materials and Structures, 2015, 24(1): 015002
Duan R, Wang F. Fault diagnosis of on-load tap-changer in converter transformer based on time-frequency vibration analysis. IEEE Transactions on Industrial Electronics, 2016, 63(6): 3815–3823
Feng Z, Ma H, Zuo MJ. Vibration signal models for fault diagnosis of planet bearings. Journal of Sound and Vibration, 2016, 370: 372–393
Kumar H, Sugumaran V, Amarnath M. Fault diagnosis of bearings through sound signal using statistical features and bayes classifier. Journal of Vibration Engineering & Technologies, 2016, 4(2): 87–96
Lu S, Wang X, He Q, et al. Fault diagnosis of motor bearing with speed fluctuation via angular resampling of transient sound signals. Journal of Sound and Vibration, 2016, 385: 16–32
Pahon E, Yousfi-Steiner N, Jemei S, et al. A non-intrusive signalbased method for a proton exchange membrane fuel cell fault diagnosis. Fuel Cells, 2016, 17: 238–246
Pei P, Li Y, Xu H, et al. A review on water fault diagnosis of PEMFC associated with the pressure drop. Applied Energy, 2016, 173: 366–385
Ohtsu M, Enoki M, Mizutani Y, et al. Principles of the acoustic emission (AE) method and signal processing. In The Japanese Society for Non-Destructive Inspection, ed. Practical Acoustic Emission Testing. Tokyo: Springer, 2016, 5–34
Cong F, Chen J, Dong G, et al. Vibration model of rolling element bearings in a rotor-bearing system for fault diagnosis. Journal of Sound and Vibration, 2013, 332(8): 2081–2097
Yoon J, He D, Van Hecke B. On the use of a single piezoelectric strain sensor for wind turbine planetary gearbox fault diagnosis. IEEE Transactions on Industrial Electronics, 2015, 62(10): 6585–6593
Wei P, Dai Z, Zheng L, et al. Fault diagnosis of the rolling bearing with optical fiber Bragg grating vibration sensor. Proceedings of SPIE: Optical Measurement Technology and Instrumentation, 2016, 101552I
Su Z, Ye L. Identification of damage using Lamb waves. London: Springer, 2009
Lynch J P, Loh K J. A summary review of wireless sensors and sensor networks for structural health monitoring. Shock and Vibration Digest, 2006, 38(2): 91–128
Huang J, Chen G, Shu L, et al. WSNs-based mechanical equipment state monitoring and fault diagnosis in China. International Journal of Distributed Sensor Networks, 2015, 2015: 528464
Ricci R, Pennacchi P. Diagnostics of gear faults based on EMD and automatic selection of intrinsic mode functions. Mechanical Systems and Signal Processing, 2011, 25(3): 821–838
Mehrjou M R, Mariun N, Hamiruce Marhaban M, et al. Rotor fault condition monitoring techniques for squirrel-cage induction machine—A review. Mechanical Systems and Signal Processing, 2011, 25(8): 2827–2848
Randall R B, Antoni J. Rolling element bearing diagnostics—A tutorial. Mechanical Systems and Signal Processing, 2011, 25(2): 485–520
Zhang Y, Randall R. Rolling element bearing fault diagnosis based on the combination of genetic algorithms and fast kurtogram. Mechanical Systems and Signal Processing, 2009, 23(5): 1509–1517
Boškoski P, Petrovčič J, Musizza B, et al. Detection of lubrication starved bearings in electrical motors by means of vibration analysis. Tribology International, 2010, 43(9): 1683–1692
Borghesani P, Pennacchi P, Chatterton S. The relationship between kurtosis-and envelope-based indexes for the diagnostic of rolling element bearings. Mechanical Systems and Signal Processing, 2014, 43(1–2): 25–43
Wang Y, Xiang J, Markert R, et al. Spectral kurtosis for fault detection, diagnosis and prognostics of rotating machines: A review with applications. Mechanical Systems and Signal Processing, 2016, 66–67: 679–698
Barszcz T, Randall R B. Application of spectral kurtosis for detection of a tooth crack in the planetary gear of a wind turbine. Mechanical Systems and Signal Processing, 2009, 23(4): 1352–1365
Dwyer R. Detection of non-Gaussian signals by frequency domain kurtosis estimation. In Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing. Boston: IEEE, 1983, 607–610
Dwyer R. Use of the kurtosis statistic in the frequency domain as an aid in detecting random signals. IEEE Journal of Oceanic Engineering, 1984, 9(2): 85–92
Vrabie V, Granjon P, Serviere C. Spectral kurtosis: From definition to application. In Proceedings of 6th IEEE InternationalWorkshop on Nonlinear Signal and Image Processing (NSIP 2003). Grado-Trieste: IEEE, 2003
Antoni J. The spectral kurtosis: A useful tool for characterising non-stationary signals. Mechanical Systems and Signal Processing, 2006, 20(2): 282–307
Antoni J, Randall R. The spectral kurtosis: Application to the vibratory surveillance and diagnostics of rotating machines. Mechanical Systems and Signal Processing, 2006, 20(2): 308–331
Antoni J. Fast computation of the kurtogram for the detection of transient faults. Mechanical Systems and Signal Processing, 2007, 21(1): 108–124
Randall R. Applications of spectral kurtosis in machine diagnostics and prognostics. Key Engineering Materials, 2005, 293–294: 21–32
Liu H, Huang W, Wang S, et al. Adaptive spectral kurtosis filtering based on Morlet wavelet and its application for signal transients detection. Signal Process, 2014, 96, Part A: 118–124
Lei Y, Lin J, He Z, et al. Application of an improved kurtogram method for fault diagnosis of rolling element bearings. Mechanical Systems and Signal Processing, 2011, 25(5): 1738–1749
Wang Y, Liang M. An adaptive SK technique and its application for fault detection of rolling element bearings. Mechanical Systems and Signal Processing, 2011, 25(5): 1750–1764
Barszcz T, JabŁoński A. A novel method for the optimal band selection for vibration signal demodulation and comparison with the Kurtogram. Mechanical Systems and Signal Processing, 2011, 25(1): 431–451
Borghesani P, Pennacchi P, Randall R, et al. Application of cepstrum pre-whitening for the diagnosis of bearing faults under variable speed conditions. Mechanical Systems and Signal Processing, 2013, 36(2): 370–384
Smith W A, Fan Z, Peng Z, et al. Optimised spectral kurtosis for bearing diagnostics under electromagnetic interference. Mechanical Systems and Signal Processing, 2016, 75: 371–394
Wang D, Tse P W, Tsui K L. An enhanced kurtogram method for fault diagnosis of rolling element bearings. Mechanical Systems and Signal Processing, 2013, 35(1–2): 176–199
Sawalhi N, Randall R, Endo H. The enhancement of fault detection and diagnosis in rolling element bearings using minimum entropy deconvolution combined with spectral kurtosis. Mechanical Systems and Signal Processing, 2007, 21(6): 2616–2633
He D, Wang X, Li S, et al. Identification of multiple faults in rotating machinery based on minimum entropy deconvolution combined with spectral kurtosis. Mechanical Systems and Signal Processing, 2016, 81: 235–249
Luo J, Yu D, Liang M. A kurtosis-guided adaptive demodulation technique for bearing fault detection based on tunable-Q wavelet transform. Measurement Science & Technology, 2013, 24(5): 055009
Patel V, Tandon N, Pandey R. Defect detection in deep groove ball bearing in presence of external vibration using envelope analysis and Duffing oscillator. Measurement, 2012, 45(5): 960–970
Tian J, Morillo C, Azarian MH, et al. Motor bearing fault detection using spectral kurtosis-based feature extraction coupled with Knearest neighbor distance analysis. IEEE Transactions on Industrial Electronics, 2016, 63(3): 1793–1803
Immovilli F, Cocconcelli M, Bellini A, et al. Detection of generalized-roughness bearing fault by spectral-kurtosis energy of vibration or current signals. IEEE Transactions on Industrial Electronics, 2009, 56(11): 4710–4717
Leite V C M N, Borges da Silva J G, Veloso G F C, et al. Detection of localized bearing faults in induction machines by spectral kurtosis and envelope analysis of stator current. IEEE Transactions on Industrial Electronics, 2015, 62(3): 1855–1865
Fournier E, Picot A, Régnier J, et al. Current-based detection of mechanical unbalance in an induction machine using spectral kurtosis with reference. IEEE Transactions on Industrial Electronics, 2015, 62(3): 1879–1887
Eftekharnejad B, Carrasco M, Charnley B, et al. The application of spectral kurtosis on acoustic emission and vibrations from a defective bearing. Mechanical Systems and Signal Processing, 2011, 25(1): 266–284
Ruiz-Cárcel C, Hernani-Ros E, Cao Y, et al. Use of spectral kurtosis for improving signal to noise ratio of acoustic emission signal from defective bearings. Journal of Failure Analysis and Prevention, 2014, 14(3): 363–371
Johnson J T, Potter L C. Performance study of algorithms for detecting pulsed sinusoidal interference in microwave radiometry. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47 (2): 628–636
Dion J L, Tawfiq I, Chevallier G. Harmonic component detection: Optimized Spectral Kurtosis for operational modal analysis. Mechanical Systems and Signal Processing, 2012, 26: 24–33
Lee J H, Seo J S. Application of spectral kurtosis to the detection of tip vortex cavitation noise in marine propeller. Mechanical Systems and Signal Processing, 2013, 40(1): 222–236
Nita G M, Gary D E. Statistics of the spectral kurtosis estimator. Publications of the Astronomical Society of the Pacific, 2010, 122 (891): 595–607
Millioz F, Martin N. Circularity of the STFT and spectral kurtosis for time-frequency segmentation in Gaussian environment. IEEE Transactions on Signal Processing, 2011, 59(2): 515–524
Antoni J, Randall R. Differential diagnosis of gear and bearing faults. Journal of Vibration and Acoustics, 2002, 124(2): 165–171
Cui L, Wang J, Lee S. Matching pursuit of an adaptive impulse dictionary for bearing fault diagnosis. Journal of Sound and Vibration, 2014, 333(10): 2840–2862
He G, Ding K, Lin H. Fault feature extraction of rolling element bearings using sparse representation. Journal of Sound and Vibration, 2016, 366: 514–527
Tang H, Chen J, Dong G. Sparse representation based latent components analysis for machinery weak fault detection. Mechanical Systems and Signal Processing, 2014, 46(2): 373–388
Zhang H, Chen X, Du Z, et al. Nonlocal sparse model with adaptive structural clustering for feature extraction of aero-engine bearings. Journal of Sound and Vibration, 2016, 368: 223–248
Zhang H, Chen X, Du Z, et al. Kurtosis based weighted sparse model with convex optimization technique for bearing fault diagnosis. Mechanical Systems and Signal Processing, 2016, 80: 349–376
He Q, Ding X. Sparse representation based on local time-frequency template matching for bearing transient fault feature extraction. Journal of Sound and Vibration, 2016, 370: 424–443
Wang S, Cai G, Zhu Z, et al. Transient signal analysis based on Levenberg-Marquardt method for fault feature extraction of rotating machines. Mechanical Systems and Signal Processing, 2015, 54–55: 16–40
Wang S, Huang W, Zhu Z. Transient modeling and parameter identification based on wavelet and correlation filtering for rotating machine fault diagnosis. Mechanical Systems and Signal Processing, 2011, 25(4): 1299–1320
Fan W, Cai G, Zhu Z, et al. Sparse representation of transients in wavelet basis and its application in gearbox fault feature extraction. Mechanical Systems and Signal Processing, 2015, 56–57: 230–245
Qiao B, Zhang X, Gao J, et al. Sparse deconvolution for the largescale ill-posed inverse problem of impact force reconstruction. Mechanical Systems and Signal Processing, 2016, 83: 93–115
Qiao B, Zhang X, Wang C, et al. Sparse regularization for force identification using dictionaries. Journal of Sound and Vibration, 2016, 368: 71–86
Lin J, Hu Z, Chen Z, et al. Sparse reconstruction of blade tip-timing signals for multi-mode blade vibration monitoring. Mechanical Systems and Signal Processing, 2016, 81: 250–258
Ding Y, He W, Chen B, et al. Detection of faults in rotating machinery using periodic time-frequency sparsity. Journal of Sound and Vibration, 2016, 382: 357–378
He W, Ding Y, Zi Y, et al. Sparsity-based algorithm for detecting faults in rotating machines. Mechanical Systems and Signal Processing, 2016, 72–73: 46–64
He W, Ding Y, Zi Y, et al. Repetitive transients extraction algorithm for detecting bearing faults. Mechanical Systems and Signal Processing, 2017, 84, Part A: 227–244
Donoho D L. Compressed sensing. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306
Tang G, Yang Q, Wang H, et al. Sparse classification of rotating machinery faults based on compressive sensing strategy. Mechatronics, 2015, 31: 60–67
Chen X, Du Z, Li J, et al. Compressed sensing based on dictionary learning for extracting impulse components. Signal Process, 2014, 96, Part A: 94–109
Du Z, Chen X, Zhang H, et al. Sparse feature identification based on union of redundant dictionary for wind turbine gearbox fault diagnosis. IEEE Transactions on Industrial Electronics, 2015, 62 (10): 6594–6605
Chen X, Cai G, Cao H, et al. Condition assessment for automatic tool changer based on sparsity-enabled signal decomposition method. Mechatronics, 2015, 31: 50–59
Wang Y, Xiang J, Mo Q, et al. Compressed sparse time-frequency feature representation via compressive sensing and its applications in fault diagnosis. Measurement, 2015, 68: 70–81
Qiao B, Zhang X, Gao J, et al. Impact-force sparse reconstruction from highly incomplete and inaccurate measurements. Journal of Sound and Vibration, 2016, 376: 72–94
Feng Z, Liang M, Chu F. Recent advances in time-frequency analysis methods for machinery fault diagnosis: A review with application examples. Mechanical Systems and Signal Processing, 2013, 38(1): 165–205
Peng Z, Chu F. Application of the wavelet transform in machine condition monitoring and fault diagnostics: A review with bibliography. Mechanical Systems and Signal Processing, 2004, 18(2): 199–221
Yan R, Gao R X, Chen X. Wavelets for fault diagnosis of rotary machines: A review with applications. Signal Processing, 2014, 96: 1–15
Auger F, Flandrin P, Lin Y T, et al. Time-frequency reassignment and synchrosqueezing: An overview. IEEE Signal Processing Magazine, 2013, 30(6): 32–41
Daubechies I, Lu J,Wu H T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. Applied and Computational Harmonic Analysis, 2011, 30(2): 243–261
Li C, Liang M. Time-frequency signal analysis for gearbox fault diagnosis using a generalized synchrosqueezing transform. Mechanical Systems and Signal Processing, 2012, 26: 205–217
Li C, Liang M. A generalized synchrosqueezing transform for enhancing signal time-frequency representation. Signal Processing, 2012, 92(9): 2264–2274
Feng Z, Chen X, Liang M. Iterative generalized synchrosqueezing transform for fault diagnosis of wind turbine planetary gearbox under nonstationary conditions. Mechanical Systems and Signal Processing, 2015, 52–53: 360–375
Shi J, Liang M, Necsulescu D S, et al. Generalized stepwise demodulation transform and synchrosqueezing for time-frequency analysis and bearing fault diagnosis. Journal of Sound and Vibration, 2016, 368: 202–222
Cao H, Xi S, Chen X, et al. Zoom synchrosqueezing transform and iterative demodulation: Methods with application. Mechanical Systems and Signal Processing, 2016, 72–73: 695–711
Wang S, Chen X, Li G, et al. Matching demodulation transform with application to feature extraction of rotor rub-impact fault. IEEE Transactions on Instrumentation and Measurement, 2014, 63 (5): 1372–1383
Sheu Y L, Hsu L Y, Wu H T. Analysis of signals with fast-varying instantaneous frequency: Window selection and insights from synchrosqueezing transform. arXiv preprint arXiv:1512.04811, 2015
Wang S, Chen X, Tong C, et al. Matching synchrosqueezing wavelet transform and application to aeroengine vibration monitoring. IEEE Transactions on Instrumentation and Measurement, 2017, 66(2): 360–372
Wang S, Chen X, Wang Y, et al. Nonlinear squeezing timefrequency transform for weak signal detection. Signal Processing, 2015, 113: 195–210
Wang S, Yang L, Chen X, et al. Nonlinear squeezing timefrequency transform and application in rotor rub-impact fault diagnosis. Journal of Manufacturing Science and Engineering, 2017 (in press)
Peng Z, Meng G, Chu F, et al. Polynomial chirplet transform with application to instantaneous frequency estimation. IEEE Transactions on Instrumentation and Measurement, 2011, 60(9): 3222–3229
Yang Y, Zhang W, Peng Z, et al. Multicomponent signal analysis based on polynomial chirplet transform. IEEE Transactions on Industrial Electronics, 2013, 60(9): 3948–3956
Yang Y, Peng Z, Meng G, et al. Spline-kernelled Chirplet transform for the analysis of signals with time-varying frequency and its application. IEEE Transactions on Industrial Electronics, 2012, 59(3): 1612–1621
Yang Y, Peng Z, Meng G, et al. Characterize highly oscillating frequency modulation using generalized Warblet transform. Mechanical Systems and Signal Processing, 2012, 26: 128–140
Yang Y, Peng Z, Dong X, et al. General parameterized timefrequency transform. IEEE Transactions on Signal Processing, 2014, 62(11): 2751–2764
Yang Y, Peng Z, Dong X, et al. Application of parameterized timefrequency analysis on multicomponent frequency modulated signals. IEEE Transactions on Instrumentation and Measurement, 2014, 63(12): 3169–3180
Yang W, Tavner P J, Tian W. Wind turbine condition monitoring based on an improved spline-kernelled chirplet transform. IEEE Transactions on Industrial Electronics, 2015, 62(10): 6565–6574
Yang Y, Peng Z, Zhang W, et al. Dispersion analysis for broadband guided wave using generalized Warblet transform. Journal of Sound and Vibration, 2016, 367: 22–36
Yang Y, Peng Z, Dong X, et al. Nonlinear time-varying vibration system identification using parametric time-frequency transform with spline kernel. Nonlinear Dynamics, 2016, 85(3): 1679–1693
Wang S, Chen X, Cai G, et al. Matching demodulation transform and synchrosqueezing in time-frequency analysis. IEEE Transactions on Signal Processing, 2014, 62(1): 69–84
Bouzida A, Touhami O, Ibtiouen R, et al. Fault diagnosis in industrial induction machines through discrete wavelet transform. IEEE Transactions on Industrial Electronics, 2011, 58(9): 4385–4395
Bin G, Gao J, Li X, et al. Early fault diagnosis of rotating machinery based on wavelet packets—Empirical mode decomposition feature extraction and neural network. Mechanical Systems and Signal Processing, 2012, 27: 696–711
Seshadrinath J, Singh B, Panigrahi B K. Investigation of vibration signatures for multiple fault diagnosis in variable frequency drives using complex wavelets. IEEE Transactions on Power Electronics, 2014, 29(2): 936–945
Bayram I, Selesnick I W. Overcomplete discrete wavelet transforms with rational dilation factors. IEEE Transactions on Signal Processing, 2009, 57(1): 131–145
Bayram I, Selesnick I W. Frequency-domain design of overcomplete rational-dilation wavelet transforms. IEEE Transactions on Signal Processing, 2009, 57(8): 2957–2972
Selesnick I W. Wavelet transform with tunable Q-factor. IEEE Transactions on Signal Processing, 2011, 59(8): 3560–3575
Chen B, Zhang Z, Sun C, et al. Fault feature extraction of gearbox by using overcomplete rational dilation discrete wavelet transform on signals measured from vibration sensors. Mechanical Systems and Signal Processing, 2012, 33: 275–298
He W, Zi Y, Chen B, et al. Tunable Q-factor wavelet transform denoising with neighboring coefficients and its application to rotating machinery fault diagnosis. Science China. Technological Sciences, 2013, 56(8): 1956–1965
Wang H, Chen J, Dong G. Feature extraction of rolling bearing’s early weak fault based on EEMD and tunable Q-factor wavelet transform. Mechanical Systems and Signal Processing, 2014, 48 (1–2): 103–119
Wang X, Zi Y, He Z. Multiwavelet denoising with improved neighboring coefficients for application on rolling bearing fault diagnosis. Mechanical Systems and Signal Processing, 2011, 25 (1): 285–304
Yuan J, He Z, Zi Y, et al. Construction and selection of liftingbased multiwavelets for mechanical fault detection. Mechanical Systems and Signal Processing, 2013, 40(2): 571–588
Jiang H, Li C, Li H. An improved EEMD with multiwavelet packet for rotating machinery multi-fault diagnosis. Mechanical Systems and Signal Processing, 2013, 36(2): 225–239
Sun H, He Z, Zi Y, et al. Multiwavelet transform and its applications in mechanical fault diagnosis—A review. Mechanical Systems and Signal Processing, 2014, 43(1–2): 1–24
Lei Y, Lin J, He Z, et al. A review on empirical mode decomposition in fault diagnosis of rotating machinery. Mechanical Systems and Signal Processing, 2013, 35(1–2): 108–126
Babu T R, Srikanth S, Sekhar A S. Hilbert-Huang transform for detection and monitoring of crack in a transient rotor. Mechanical Systems and Signal Processing, 2008, 22(4): 905–914
Lin L, Chu F. HHT-based AE characteristics of natural fatigue cracks in rotating shafts. Mechanical Systems and Signal Processing, 2012, 26: 181–189
Guo D, Peng Z. Vibration analysis of a cracked rotor using Hilbert-Huang transform. Mechanical Systems and Signal Processing, 2007, 21(8): 3030–3041
Zhang K, Yan X. Multi-cracks identification method for cantilever beam structure with variable cross-sections based on measured natural frequency changes. Journal of Sound and Vibration, 2017, 387: 53–65
Chandra N H, Sekhar A. Fault detection in rotor bearing systems using time frequency techniques. Mechanical Systems and Signal Processing, 2016, 72–73: 105–133
Xu L. Study on fault detection of rolling element bearing based on translation-invariant denoising and Hilbert-Huang transform. Journal of Computers, 2012, 7(5): 1142–1146
Li Q, Wang H. A research review of Hilbert-Huang transform used for rolling bearing fault diagnosis. Applied Mechanics and Materials, 2013, 397–400: 2152–2155
Lei Y, He Z, Zi Y. Application of the EEMD method to rotor fault diagnosis of rotating machinery. Mechanical Systems and Signal Processing, 2009, 23(4): 1327–1338
Feng Z, Zuo M J, Hao R, et al. Ensemble empirical mode decomposition-based Teager energy spectrum for bearing fault diagnosis. Journal of Vibration and Acoustics, 2013, 135(3): 031013
Wu T Y, Chen J, Wang C. Characterization of gear faults in variable rotating speed using Hilbert-Huang transform and instantaneous dimensionless frequency normalization. Mechanical Systems and Signal Processing, 2012, 30: 103–122
Smith J S. The local mean decomposition and its application to EEG perception data. Journal of the Royal Society, Interface, 2005, 2(5): 443–454
Wang Y, He Z, Zi Y. A demodulation method based on improved local mean decomposition and its application in rub-impact fault diagnosis. Measurement Science and Technology, 2009, 20(2): 025704
Cheng J, Yang Y, Yang Y. A rotating machinery fault diagnosis method based on local mean decomposition. Digital Signal Processing, 2012, 22(2): 356–366
Feng Z, Zuo M J, Qu J, et al. Joint amplitude and frequency demodulation analysis based on local mean decomposition for fault diagnosis of planetary gearboxes. Mechanical Systems and Signal Processing, 2013, 40(1): 56–75
Liu H, Han M. A fault diagnosis method based on local mean decomposition and multi-scale entropy for roller bearings. Mechanism and Machine Theory, 2014, 75: 67–78
Wang Y, Markert R, Xiang J, et al. Research on variational mode decomposition and its application in detecting rub-impact fault of the rotor system. Mechanical Systems and Signal Processing, 2015, 60–61: 243–251
Widodo A, Yang B S. Support vector machine in machine condition monitoring and fault diagnosis. Mechanical Systems and Signal Processing, 2007, 21(6): 2560–2574
Jardine A K S, Lin D, Banjevic D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mechanical Systems and Signal Processing, 2006, 20(7): 1483–1510
Jia F, Lei Y, Lin J, et al. Deep neural networks: A promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data. Mechanical Systems and Signal Processing, 2016, 72–73: 303–315
Roemer M J, Hong C, Hesler S H. Machine health monitoring and life management using finite-element-based neural networks. Journal of Engineering for Gas Turbines and Power, 1996, 118 (4): 830–835
Li B, Chow M Y, Tipsuwan Y, et al. Neural-network-based motor rolling bearing fault diagnosis. IEEE Transactions on Industrial Electronics, 2000, 47(5): 1060–1069
Fan Y, Li C J. Diagnostic rule extraction from trained feedforward neural networks. Mechanical Systems and Signal Processing, 2002, 16(6): 1073–1081
Gebraeel N Z, Lawley M A. A neural network degradation model for computing and updating residual life distributions. IEEE Transactions on Automation Science and Engineering, 2008, 5(1): 154–163
Vyas N S, Satishkumar D. Artificial neural network design for fault identification in a rotor-bearing system. Mechanism and Machine Theory, 2001, 36(2): 157–175
Jack L, Nandi A. Comparison of neural networks and support vector machines in condition monitoring applications. In: Proceedings of 13th International Congress on Condition Monitoring and Diagnostic Engineering Management. 2000, 721–730
Saravanan N, Siddabattuni V K, Ramachandran K. Fault diagnosis of spur bevel gear box using artificial neural network (ANN), and proximal support vector machine (PSVM). Applied Soft Computing, 2010, 10(1): 344–360
Nguyen N T, Lee H H, Kwon J M. Optimal feature selection using genetic algorithm for mechanical fault detection of induction motor. Journal of Mechanical Science and Technology, 2008, 22 (3): 490–496
Spoerre J. Application of the cascade correlation algorithm (CCA) to bearing fault classification problems. Computers in Industry, 1997, 32(3): 295–304
Baillie D, Mathew J. A comparison of autoregressive modeling techniques for fault diagnosis of rolling element bearings. Mechanical Systems and Signal Processing, 1996, 10(1): 1–17
Li C J, Huang T Y. Automatic structure and parameter training methods for modeling of mechanical systems by recurrent neural networks. Applied Mathematical Modelling, 1999, 23(12): 933–944
Deuszkiewicz P, Radkowski S. On-line condition monitoring of a power transmission unit of a rail vehicle. Mechanical Systems and Signal Processing, 2003, 17(6): 1321–1334
Nyanteh Y D. Application of artificial intelligence to rotating machine condition monitoring. Dissertation for the Doctoral Degree. Tallahassee: The Florida State University, 2013
Samanta B. Artificial neural networks and genetic algorithms for gear fault detection. Mechanical Systems and Signal Processing, 2004, 18(5): 1273–1282
Wang C C, Too G P J. Rotating machine fault detection based on HOS and artificial neural networks. Journal of Intelligent Manufacturing, 2002, 13(4): 283–293
Wang H, Gao J, Jiang Z, et al. Rotating machinery fault diagnosis based on EEMD time-frequency energy and SOM neural network. Arabian Journal for Science and Engineering, 2014, 39(6): 5207–5217
Yang D, Liu Y, Li S, et al. Gear fault diagnosis based on support vector machine optimized by artificial bee colony algorithm. Mechanism and Machine Theory, 2015, 90: 219–229
Widodo A, Kim E Y, Son J D, et al. Fault diagnosis of low speed bearing based on relevance vector machine and support vector machine. Expert Systems with Applications, 2009, 36(3): 7252–7261
Guo L, Chen J, Li X. Rolling bearing fault classification based on envelope spectrum and support vector machine. Journal of Vibration and Control, 2009, 15(9): 1349–1363
Liu Z, Cao H, Chen X, et al. Multi-fault classification based on wavelet SVM with PSO algorithm to analyze vibration signals from rolling element bearings. Neurocomputing, 2013, 99: 399–410
Samanta B, Nataraj C. Use of particle swarm optimization for machinery fault detection. Engineering Applications of Artificial Intelligence, 2009, 22(2): 308–316
Seera M, Lim C P, Nahavandi S, et al. Condition monitoring of induction motors: A review and an application of an ensemble of hybrid intelligent models. Expert Systems with Applications, 2014, 41(10): 4891–4903
Shen C, Wang D, Kong F, et al. Fault diagnosis of rotating machinery based on the statistical parameters of wavelet packet paving and a generic support vector regressive classifier. Measurement, 2013, 46(4): 1551–1564
Tabrizi A, Garibaldi L, Fasana A, et al. Early damage detection of roller bearings using wavelet packet decomposition, ensemble empirical mode decomposition and support vector machine. Meccanica, 2015, 50(3): 865–874
Rajeswari C, Sathiyabhama B, Devendiran S, et al. Diagnostics of gear faults using ensemble empirical mode decomposition, hybrid binary bat algorithm and machine learning algorithms. Journal of Vibroengineering, 2015, 17(3): 1169–1187
Tran V T, AlThobiani F, Ball A. An approach to fault diagnosis of reciprocating compressor valves using Teager-Kaiser energy operator and deep belief networks. Expert Systems with Applications, 2014, 41(9): 4113–4122
Ma M, Chen X, Wang S, et al. Bearing degradation assessment based on weibull distribution and deep belief network. In: Proceedings of International Symposium on Flexible Automation (ISFA). Cleveland: IEEE, 382–385
Tao J, Liu Y, Yang D. Bearing fault diagnosis based on deep belief network and multisensor information fusion. Shock and Vibration, 2016, 2016: 1–9
Chen Z, Li C, Sánchez R V. Multi-layer neural network with deep belief network for gearbox fault diagnosis. Journal of Vibroengineering, 2015, 17(5): 2379–2392
Shao S, Sun W, Wang P, et al. Learning features from vibration signals for induction motor fault diagnosis. In Proceedings of International Symposium on Flexible Automation (ISFA). Cleveland: IEEE, 2016, 71–76
Tamilselvan P, Wang P. Failure diagnosis using deep belief learning based health state classification. Reliability Engineering & System Safety, 2013, 115: 124–135
Gan M, Wang C. Construction of hierarchical diagnosis network based on deep learning and its application in the fault pattern recognition of rolling element bearings. Mechanical Systems and Signal Processing, 2016, 72–73: 92–104
Li C, Sánchez R V, Zurita G, et al. Fault diagnosis for rotating machinery using vibration measurement deep statistical feature learning. Sensors (Basel), 2016, 16(6): 895
Guo X, Shen C, Chen L. Deep fault recognizer: An integrated model to denoise and extract features for fault diagnosis in rotating machinery. Applied Sciences, 2016, 7(1): 41
Ahmed H, Wong M D, Nandi A. Effects of deep neural network parameters on classification of bearing faults. In: Proceedings of 42nd Annual Conference of the IEEE on Industrial Electronics Society. IEEE, 2016, 6329–6334
Xin G, Antoni J, Hamzaoui N. An exploring study of hidden Markov model in rolling element bearing diagnostis. In: Proceedings of Surveillance 8. Roanne, 2015
Bunks C, McCarthy D, Al-Ani T. Condition-based maintenance of machines using hidden Markov models. Mechanical Systems and Signal Processing, 2000, 14(4): 597–612
Dong M, He D. Hidden semi-Markov models for machinery health diagnosis and prognosis transactions of NAMRI. Transactions of the North American Manufacturing Research Institute of SME, 2004, 32: 199–206
Xu Y, Ge M. Hidden Markov model-based process monitoring system. Journal of Intelligent Manufacturing, 2004, 15(3): 337–350
Ye D, Ding Q, Wu Z. New method for faults diagnosis of rotating machinery based on 2-dimension hidden Markov model. In: Proceedings of the International Symposium on Precision Mechanical Measurement. 2002, 391–395
Zhou H, Chen J, Dong G, et al. Detection and diagnosis of bearing faults using shift-invariant dictionary learning and hidden Markov model. Mechanical Systems and Signal Processing, 2016, 72–73: 65–79
Baydar N, Chen Q, Ball A, et al. Detection of incipient tooth defect in helical gears using multivariate statistics. Mechanical Systems and Signal Processing, 2001, 15(2): 303–321
Gómez González A, Fassois S D. A supervised vibration-based statistical methodology for damage detection under varying environmental conditions & its laboratory assessment with a scale wind turbine blade. Journal of Sound and Vibration, 2016, 366: 484–500
Mao Z, Todd M. A model for quantifying uncertainty in the estimation of noise-contaminated measurements of transmissibility. Mechanical Systems and Signal Processing, 2012, 28: 470–481
Song L, Chen P, Wang H, et al. Intelligent condition diagnosis method for rotating machinery based on probability density and discriminant analyses. IEEE Signal Processing Letters, 2016, 23 (8): 1111–1115
Lei Y, He Z, Zi Y. A new approach to intelligent fault diagnosis of rotating machinery. Expert Systems with Applications, 2008, 35 (4): 1593–1600
Wang C C, Kang Y, Liao C C. Using Bayesian networks in gear fault diagnosis. Applied Mechanics and Materials, 2013, 284–287: 2416–2420
Mao Z, Todd M D. A Bayesian recursive framework for ballbearing damage classification in rotating machinery. Structural Health Monitoring, 2016, 15(6): 668–684
Wang D, Sun S, Tse P W. A general sequential Monte Carlo method based optimal wavelet filter: A Bayesian approach for extracting bearing fault features. Mechanical Systems and Signal Processing, 2015, 52–53: 293–308
Wang D, Tsui K L, Zhou Q. Novel Gauss-Hermite integration based Bayesian inference on optimal wavelet parameters for bearing fault diagnosis. Mechanical Systems and Signal Processing, 2016, 72–73: 80–91
Qu L, Liu X, Peyronne G, et al. The holospectrum: A new method for rotor surveillance and diagnosis. Mechanical Systems and Signal Processing, 1989, 3(3): 255–267
Qu L, Qiu H, Xu G. Rotor balancing based on holospectrum analysis principle and practice. China Mechanical Engineering, 1998, 9(1): 60–63 (in Chinese)
Liu S, Qu L. A new field balancing method of rotor systems based on holospectrum and genetic algorithm. Applied Soft Computing, 2008, 8(1): 446–455
Li B, Chen X, Ma J, et al. Detection of crack location and size in structures using wavelet finite element methods. Journal of Sound and Vibration, 2005, 285(4–5): 767–782
Xiang J, Chen X, Li B, et al. Identification of a crack in a beam based on the finite element method of a B-spline wavelet on the interval. Journal of Sound and Vibration, 2006, 296(4–5): 1046–1052
Xiang J, Chen X, Mo Q, et al. Identification of crack in a rotor system based on wavelet finite element method. Finite Elements in Analysis and Design, 2007, 43(14): 1068–1081
Chen X, Yang S, Ma J, et al. The construction of wavelet finite element and its application. Finite Elements in Analysis and Design, 2004, 40(5–6): 541–554
Gao J, Ma B, Jiang Z. Research on fault self-recovery engineering. Journal of Dalian University of Technology, 2006, 46(3): 460–468 (in Chinese)
Gao J. Thinking about future plant medicine engineering. Engineering Science, 2003, 5(12): 30–35 (in Chinese)
Gao J. Research on the fault self-recovery principle of equipment system. Engineering Science, 2005, 7(5): 43–48 (in Chinese)
Wen B. Recent development of vibration utilization engineering. Frontiers of Mechanical Engineering in China, 2008, 3(1): 1–9
Wen B, Li Y, Zhang Y, et al. Vibration Utilization Engineering. Beijing: Science Press, 2005 (in Chinese)
Wen B, Zhao C, Su D, et al. Vibration Synchronization and Controlled Synchronization. Beijing: Science Press, 2003 (in Chinese)
Wen B, Liu S, He Q. Theory and Dynamic Design Methods of Vibrating Machinery. Beijing: Mechanical Industry Press, 2001 (in Chinese)
Wen B, Liu F. Theory of Vibrating Machines and Its Applications. Beijing: Machine Press, 1982 (in Chinese)
NSFC. 2017. Retrieved from http://npd.nsfc.gov.cn/
Center for Intelligent Maintenance Systems. 2017. Retrieved from http://www.imscenter.net/
Acknowledgements
This work was partly supported by the National Key Basic Research Program of China (Grant No. 2015CB057400), the National Natural Science Foundation of China (Grant Nos. 51421004 and 51605366), and by the Fundamental Research Funds for the Central Universities.
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is published with open access at link.springer.com and journal.hep.com.cn
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the appropriate credit is given to the original author(s) and the source, and a link is provided to the Creative Commons license, indicating if changes were made.
About this article
Cite this article
Chen, X., Wang, S., Qiao, B. et al. Basic research on machinery fault diagnostics: Past, present, and future trends. Front. Mech. Eng. 13, 264–291 (2018). https://doi.org/10.1007/s11465-018-0472-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11465-018-0472-3