Skip to main content
SpringerLink
Log in

A dynamic model of mobile concrete pump boom based on discrete time transfer matrix method

  • Research Article
  • Published:
Frontiers of Mechanical Engineering Aims and scope Submit manuscript

Abstract

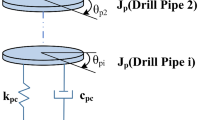
Mobile concrete pump boom is typical multibody large-scale motion manipulator. Due to posture constantly change in working process, kinematic rule and dynamic characteristic are difficult to solve. A dynamics model of a mobile concrete pump boom is established based on discrete time transfer matrix method (DTTMM). The boom system is divided into sub-structure A and substructure B. Sub-structure A is composed by the 1st boom and hydraulic actuator as well as the support. And substructure B is consists of the other three booms and corresponding hydraulic actuators. In the model, the booms and links are regarded as rigid elements and the hydraulic cylinders are equivalent to spring-damper. The booms are driven by the controllable hydraulic actuators. The overall dynamic equation and transfer matrix of the model can be assembled by sub-structures A and B. To get a precise result, step size and integration parameters are studied then. Next the tip displacement is calculated and compared with the result of ADAMS software. The displacement and rotation angle curves of the proposed method fit well with the ADAMS model. Besides it is convenient in modeling and saves time. So it is suitable for mobile concrete pump boom real-time monitoring and dynamic analysis. All of these provide reference to boom optimize and engineering application of such mechanisms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Rui X, He B, Lu Y, Lu W, Wang G. Discrete time transfer matrix method for multibody system dynamics. Multibody System Dynamics, 2005, 14(3–4): 317–344

    Article  MathSciNet  MATH  Google Scholar 

  2. Rui X, Wang G, Lu Y, Yun L. Transfer matrix method for linear multibody system. Multibody System Dynamics, 2008, 19(3): 179–207

    Article  MathSciNet  MATH  Google Scholar 

  3. Rui X T, Rong B, Wang G P, He B. Discrete time transfer matrix method for dynamics analysis of complex weapon systems. Science China Technological Sciences, 2011, 54(5): 1061–1071

    Article  MATH  Google Scholar 

  4. He B. Transfer matrix method for natural vibration analysis of tree system. Mathematical Problems in Engineering, 2012

    Google Scholar 

  5. Jiang G F, Chen ZB. Analysis of natural frequency characteristics by whole transfer matrix method for turboengine multi-rotors. Journal of Harbin Institute of Technology, 1998, 30(1): 32–35

    Google Scholar 

  6. Liu B G, Yin X G, Jian K L, Wu Y. Perturbation transfer matrix method for eigendata of one-dimensional structural system with parameter uncertainties. Applied Mathematics and Mechanics, 2003, 24(7): 801–807

    Article  MATH  Google Scholar 

  7. Gong J G, Ma Y S, Cui W S, Jin T. Numerical analysis on acoustic characteristics of automotive exhaust muffler by transfer matrix method. Journal of Vibration Engineering, 2010, 23(6): 636–641

    Google Scholar 

  8. Shi J, Tang S J, Gao F, Yang C L. Dynamics model for parachutesubmissile system based on discrete time transfer matrix method. Journal of Astronautics, 2012, 33(1): 13–18

    Google Scholar 

  9. Ding L H, Huang Q B, Wang J L, Zhang Q. Research of acoustic wave propagation characteristics in electrorheological fluids by transmission matrix method. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2010, 38(7): 5–7

    Google Scholar 

  10. Wu Q, Liu W J. Extended transfer matrix method for dynamic modeling of machine tools. Journal of Mechanical Engineering, 2010, 46(21): 69–75

    Article  Google Scholar 

  11. Dokainish M A. A new approach for plate vibrations: combination of transfer matrix and finite-element technique. Journal of Engineering for Industry, 1972, 94(2): 526–530

    Article  Google Scholar 

  12. Ohga M, Shigematsu T. Transient analysis of plates by a combined finite element-transfer matrix method. Computers & Structures, 1987, 26(4): 543–549

    Article  MATH  Google Scholar 

  13. Lee U. Vibration analysis of one-dimensional structures using the spectral transfer matrix method. Engineering Structures, 2000, 22(6): 681–690

    Article  Google Scholar 

  14. Horner G C, Pilkey W D. The Riccati Transfer Matrix Method. Virginia Univ Charlottesville Dept of Engineering Science and Systems, 1975

    Google Scholar 

  15. Kumar A S, Sankar T S. A new transfer matrix method for response analysis of large dynamic systems. Computers & Structures, 1986, 23(4): 545–552

    Article  MATH  Google Scholar 

  16. Ellakany A M, Elawadly K M, Alhamaky B N. A combined transfer matrix and analogue beam method for free vibration analysis of composite beams. Journal of Sound and Vibration, 2004, 277(4–5): 765–781

    Article  Google Scholar 

  17. Liu J, Chen X, He Z. Frequency domain active vibration control of a flexible plate based on neural networks. Frontiers of Mechanical Engineering, 2013, 8(2): 109–117

    Article  MATH  Google Scholar 

  18. Schadlbauer J, Husty M L, Caro S, Wengery P. Self-motions of 3-RPS manipulators. Frontiers of Mechanical Engineering, 2013, 8(1): 62–69

    Article  Google Scholar 

  19. Xia Q, Shi T L, Liu S Y, Wang M Y. A level set solution to the stress-based structural shape and topology optimization. Computers & Structures, 2012, 90–91: 55–64

    Article  Google Scholar 

  20. Wang E, Wu B, Hu Y, Yang S, Cheng Y. Dynamic parameter identification of tool-spindle interface based on RCSA and particle swarm optimization. Shock and Vibration, 2013, 20(1): 69–78

    Google Scholar 

  21. Wang M, Zan T, Yang Y, Fei R. Design and implementation of nonlinear TMD for chatter suppression: An application in turning processes. International Journal of Machine Tools & Manufacture, 2010, 50(5): 474–479

    Article  Google Scholar 

  22. Cheng Q, Zhang G, Gu P, Shao X. A product module identification approach based on axiomatic design and design structure matrix. Concurrent Engineering, 2012, 20(3): 185–194

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. State Key Laboratory for High Performance Complex Manufacturing, College of Mechanical and Electrical Engineering, Central South University, Changsha, 410083, China

    Wu Ren, Yunxin Wu & Zhaowei Zhang

Authors
  1. Wu Ren
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yunxin Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhaowei Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yunxin Wu.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ren, W., Wu, Y. & Zhang, Z. A dynamic model of mobile concrete pump boom based on discrete time transfer matrix method. Front. Mech. Eng. 8, 360–366 (2013). https://doi.org/10.1007/s11465-013-0280-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11465-013-0280-8

Keywords

Search

Navigation