Shape reconstruction of parallelogram flaw

Abstract

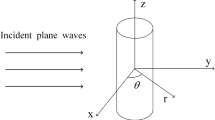
To reconstruct the shape of the scatterer in elastic media, the authors deduce the Born approximation solution of the two-dimensional scattering problem, which includes the shape factor that embodies all information about the shape of the scatterer. Accordingly, the change in the shape of the scatterer only necessitates the number of the corresponding new shape factors. For a parallelogram void in a long Al rod, its shape factor can be obtained. In view of the definition of a characteristic function, the shape factor has a corresponding integral representation. Obviously, the shape factor can be considered as a Fourier transform of the characteristic function, which is reconstructed from the inverse Fourier transform. The integral equation is considered as the basic equation to reconstruct the shape of the scatterer. The identification of the geometrical character of a flaw is then given by the two dimensional inverse Born approximation in a low-frequency range. For the parallelogram void, a theoretical calculating identification is performed. At the same time, the numerical results are obtained by the finite element method.