Abstract
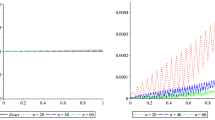
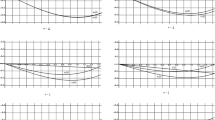
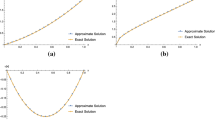
The definitions and properties of widely used fractional-order derivatives are summarized in this paper. The characteristic polynomials of the fractional-order systems are pseudo-polynomials whose powers of the complex variable are non-integers. This kind of systems can be approximated by high-order integer-order systems, and can be analyzed and designed by the sophisticated integer-order systems methodology. A new closed-form algorithm for fractional-order linear differential equations is proposed based on the definitions of fractional-order derivatives, and the effectiveness of the algorithm is illustrated through examples.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Magin R L. Fractional calculus in bioengineering. Critical Reviews in Biomedical Engineering, 2004, 32(1–2): 1–193
Podlubny I. Geometric and physical interpretation of fractional integration and fractional differentiation. Fractional Calculus & Applied Analysis, 2002, 5: 367–386
Zhao C N, Xue D Y, Chen Y Q. A fractional order PID tuning algorithm for a class of fractional order plants. In: Proceedings of the IEEE International Conference on Mechatronics and Automation, Niagara Falls. 2005, 1: 216–221
Petras I, Chen Y Q, Vinager B M. A robust stability test procedure for a class of uncertain LTI fractional order systems. In: Proceedings of International Carpathian Control Conference, Malenovice. 2002: 247–252
Xue D Y, Chen Y Q. A comparative introduction of four fractional order controllers. In: Proceedings of the 4th World Congress on Intelligent Control and Automation, Shanghai. 2002, 4: 3228–3235
Podlubny I. Fractional Differential Equations. San Diego: Academic Press, 1999
Petras I, Podlubny I, O’Leary P, et al. Analogue Realization of Fractional Order Controllers. Kosice: TU Kosice, 2002
Podlubny I. The Laplace Transform Method for Linear Differential Equations of the Fractional Order. Kosice: Slovak Academy of Science, 1994
Vinagre B M, Podlubny I, Hernández A, et al. Some approximations of fractional order operators used in control theory and applications. Fractional Calculus & Applied Analysis, 2000, 3: 231–248
Oustaloup A, Levron F, Mathieu B, et al. Frequency band complex noninteger differentiator: characterization and synthesis. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 2000, 47(1): 25–39
Chen Y Q, Vinagre B M. A new IIR-type digital fractional order differentiator. Signal Processing, 2003, 83(11): 2359–2365
Xue D, Chen Y Q. MATLAB Solutions to Advanced Mathematical Problems. Beijing: Tsinghua University Press, 2004 (in Chinese)
Author information
Authors and Affiliations
Corresponding author
Additional information
__________
Translated from Journal of Northeastern University (Natural Science), 2007, 28(1): 10–13 [译自: 东北大学学报(自然科学版)]
About this article
Cite this article
Zhao, C., Xue, D. Closed-form solutions to fractional-order linear differential equations. Front. Electr. Electron. Eng. Ch 3, 214–217 (2008). https://doi.org/10.1007/s11460-008-0025-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11460-008-0025-3