Skip to main content
SpringerLink
Log in

Fluid-driven transition from damage to fracture in anisotropic porous media: a multi-scale XFEM approach

  • Research Paper
  • Published:
Acta Geotechnica Aims and scope Submit manuscript

Abstract

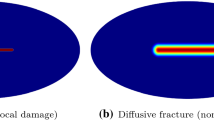
In this paper, a numerical method is proposed to simulate multi-scale fracture propagation driven by fluid injection in transversely isotropic porous media. Intrinsic anisotropy is accounted for at the continuum scale, by using a damage model in which two equivalent strains are defined to distinguish mechanical behavior in the direction parallel and perpendicular to the layer. Nonlocal equivalent strains are calculated by integration and are directly introduced in the damage evolution law. When the weighted damage exceeds a certain threshold, the transition from continuum damage to cohesive fracture is performed by dynamically inserting cohesive segments. Diffusion equations are used to model fluid flow inside the porous matrix and within the macro-fracture, in which conductivity is obtained by Darcy’s law and the cubic law, respectively. In the fractured elements, the displacement and pore pressure fields are discretized by using the XFEM technique. Interpolation on fracture elements is enriched with jump functions for displacements and with level set-based distance functions for fluid pressure, which ensures that displacements are discontinuous across the fracture, but that the pressure field remains continuous. After spatial and temporal discretization, the model is implemented in a Matlab code. Simulations are carried out in plane strain. The results validate the formulation and implementation of the proposed model and further demonstrate that it can account for material and stress anisotropy.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Abbreviations

\(\alpha (\beta )\) :

Mode I (mode II) cohesive law shape factor

\(\alpha (\varvec{x})\) :

Nonlocal weight function

\(\alpha _{ii}^t\) :

Material parameters controlling damage growth rate

\(\bar{p}\) :

Prescribed pore pressure

\(\bar{\varvec{t}}\) :

Prescribed traction on exterior boundary

\(\bar{\varvec{t}}_d\) :

Cohesive traction vector on fracture surfaces in global coordinate

\(\bar{\varvec{u}}\) :

Prescribed displacement

\(\bar{\epsilon }_i^{\rm eq}\) :

Nonlocal equivalent strain components

\(\bar{q}\) :

Prescribed flow rate

\(\bar{q}_d\) :

Flow rate difference across fracture

\(\varvec{\alpha }\) :

Biot coefficient tensor

\(\varvec{\epsilon }\) :

Strain tensor

\(\varvec{\omega }\) :

Damage variables

\(\varvec{\sigma }\) :

Stress tensor

\(\varvec{a}\) :

Enriched degree of freedom on displacement

\(\varvec{b}\) :

Enriched degree of freedom on pore pressure

\(\varvec{g}\) :

Gravity vector

\(\varvec{m}_{\varGamma _d}\) :

Unit tangent vector along fracture

\(\varvec{n}_{\varGamma _d}\) :

Unit normal vector along fracture

\(\varvec{q}\) :

Fluid flow rate

\(\varvec{s}\) :

Fracture natural coordinate

\(\varvec{v}\) :

Fluid velocity

\(\varvec{\kappa }_{\rm m}\) :

Matrix permeability tensor

\(\varDelta _n(\varDelta _t)\) :

Separations in the normal (shear) direction at current time

\(\delta _n(\delta _t)\) :

Separations in the normal (shear) direction at failure

\(\epsilon _i^{\rm eq}\) :

Local equivalent strain components

\(\epsilon _{12}^{s0}\) :

Initial out-of-bedding-plane shear strain threshold

\(\epsilon _{ii}^{t0}\) :

Initial tensile strain thresholds

\(\varGamma _{n}(\varGamma _{t})\) :

Mode I (mode II) energy constants

\(\kappa _i\) :

Internal state variables controlling damage evolution

\(\lambda _{n}(\lambda _{t})\) :

Mode I (mode II) initial slope indicator

\(\mathbb {C}\) :

Stiffness tensor

\(\mathbf M\) :

Damage operator in Voigt notation

\(\mathbf {S/C}\) :

Compliance/stiffness matrix in Voigt notation

\(\mu\) :

Fluid viscosity

\(\phi\) :

Matrix porosity

\(\phi (\varvec{x})\) :

Level set function

\(\phi _n(\phi _t)\) :

Mode I (mode II) cohesive energy release rate

\(\rho _{\text {f}}\) :

Fluid density

\(\sigma _{max}(\tau _{max})\) :

Mode I (mode II) cohesive strength

c :

Fracture hydraulic conductivity

\(H_s\) :

Helmholtz free energy

\(H_{\varGamma _d}\) :

Heaviside jump function

\(K_{\text {f}}\) :

Fluid bulk modulus

\(l_c\) :

Nonlocal internal length parameter

M :

Biot modulus

m(n):

Mode I (mode II) non-dimensional exponents

\(m_{\text {f}}\) :

Fluid mass

N :

Biot skeleton modulus

\(N_{ui}(N_{pi})\) :

Shape functions for displacement (pore pressure)

p :

Pore pressure

\(Q_{\rm in}\) :

Fluid injection rate

\(T_n(T_t)\) :

Normal (shear) cohesive traction in local coordinate

w :

Fracture aperture

References

  1. Abe H, Keer L, Mura T (1979) Theoretical study of hydraulically fractured penny-shaped cracks in hot, dry rocks. Int J Numer Anal Methods Geomech 3(1):79–96

    MATH  Google Scholar 

  2. Abe H, Keer LM, Mura T (1976) Growth rate of a penny-shaped crack in hydraulic fracturing of rocks, 2. J Geophys Res 81(35):6292–6298

    Google Scholar 

  3. Adachi JI, Detournay E (2002) Self-similar solution of a plane-strain fracture driven by a power-law fluid. Int J Numer Anal Methods Geomech 26(6):579–604

    MATH  Google Scholar 

  4. Adachi JI, Detournay E (2008) Plane strain propagation of a hydraulic fracture in a permeable rock. Eng Fract Mech 75(16):4666–4694

    Google Scholar 

  5. Advani S, Lee T, Lee J (1990) Three-dimensional modeling of hydraulic fractures in layered media: Part I—finite element formulations. J Energy Resourc Technol 112(1):1–9

    Google Scholar 

  6. Biot MA (1941) General theory of three-dimensional consolidation. J Appl Phys 12(2):155–164

    MATH  Google Scholar 

  7. Bunger AP, Detournay E (2005) Asymptotic solution for a penny-shaped near-surface hydraulic fracture. Eng Fract Mech 72(16):2468–2486

    Google Scholar 

  8. Bunger AP, Detournay E (2007) Early-time solution for a radial hydraulic fracture. J Eng Mech 133(5):534–540

    Google Scholar 

  9. Carter B, Desroches J, Ingraffea A, Wawrzynek P (2000) Simulating fully 3d hydraulic fracturing. Model Geomech 200:525–557

    Google Scholar 

  10. Chen Z (2012) Finite element modelling of viscosity-dominated hydraulic fractures. J Pet Sci Eng 88:136–144

    Google Scholar 

  11. Cohen CE, Kresse O, Weng X et al (2015) A new stacked height growth model for hydraulic fracturing simulation. In: 49th US rock mechanics/geomechanics symposium. American Rock Mechanics Association

  12. Comi C, Mariani S, Perego U (2007) An extended fe strategy for transition from continuum damage to mode i cohesive crack propagation. Int J Numer Anal Methods Geomech 31(2):213

    MATH  Google Scholar 

  13. Coussy O (2004) Poromechanics. Wiley, New York

    MATH  Google Scholar 

  14. Cuvilliez S, Feyel F, Lorentz E, Michel-Ponnelle S (2012) A finite element approach coupling a continuous gradient damage model and a cohesive zone model within the framework of quasi-brittle failure. Comput Methods Appl Mech Eng 237:244–259

    MathSciNet  MATH  Google Scholar 

  15. De Borst R, Réthoré J, Abellan MA (2006) A numerical approach for arbitrary cracks in a fluid-saturated medium. Arch Appl Mech 75(10–12):595–606

    MATH  Google Scholar 

  16. Desroches J, Detournay E, Lenoach B, Papanastasiou P, Pearson JRA, Thiercelin M, Cheng A (1994) The crack tip region in hydraulic fracturing. Proc R Soc Lond A 447(1929):39–48

    MATH  Google Scholar 

  17. Detournay E (2004) Propagation regimes of fluid-driven fractures in impermeable rocks. Int J Geomech 4(1):35–45

    Google Scholar 

  18. Detournay E, Peirce A (2014) On the moving boundary conditions for a hydraulic fracture. Int J Eng Sci 84:147–155

    MATH  Google Scholar 

  19. Dontsov E, Peirce A (2015) An enhanced pseudo-3d model for hydraulic fracturing accounting for viscous height growth, non-local elasticity, and lateral toughness. Eng Fract Mech 142:116–139

    Google Scholar 

  20. Dontsov E, Peirce A (2015) A non-singular integral equation formulation to analyse multiscale behaviour in semi-infinite hydraulic fractures. J Fluid Mech 781:R1

    MathSciNet  MATH  Google Scholar 

  21. Dontsov E, Peirce A (2016) Implementing a universal tip asymptotic solution into an implicit level set algorithm (ilsa) for multiple parallel hydraulic fractures. In: 50th US rock mechanics/geomechanics symposium. American Rock Mechanics Association

  22. Dontsov E, Peirce A (2017) A multiscale implicit level set algorithm (ilsa) to model hydraulic fracture propagation incorporating combined viscous, toughness, and leak-off asymptotics. Comput Methods Appl Mech Eng 313:53–84

    MathSciNet  Google Scholar 

  23. Dormieux L, Kondo D, Ulm FJ (2006) Microporomechanics. Wiley, New York

    MATH  Google Scholar 

  24. Faivre M, Paul B, Golfier F, Giot R, Massin P, Colombo D (2016) 2d coupled hm-xfem modeling with cohesive zone model and applications to fluid-driven fracture network. Eng Fract Mech 159:115–143

    Google Scholar 

  25. Fries TP (2008) A corrected xfem approximation without problems in blending elements. Int J Numer Methods Eng 75(5):503–532

    MathSciNet  MATH  Google Scholar 

  26. Gallant C, Zhang J, Wolfe CA, Freeman J, Al-Bazali TM, Reese M et al (2007) Wellbore stability considerations for drilling high-angle wells through finely laminated shale: a case study from terra nova. In: SPE annual technical conference and exhibition. Society of Petroleum Engineers

  27. Garagash D (2006) Transient solution for a plane-strain fracture driven by a shear-thinning, power-law fluid. Int J Numer Anal Methods Geomech 30(14):1439–1475

    MATH  Google Scholar 

  28. Garagash DI (2006) Plane-strain propagation of a fluid-driven fracture during injection and shut-in: asymptotics of large toughness. Eng Fract Mech 73(4):456–481

    Google Scholar 

  29. Garagash DI, Detournay E (2005) Plane-strain propagation of a fluid-driven fracture: small toughness solution. J Appl Mech 72(6):916–928

    MATH  Google Scholar 

  30. Garagash DI, Detournay E, Adachi J (2011) Multiscale tip asymptotics in hydraulic fracture with leak-off. J Fluid Mech 669:260–297

    MathSciNet  MATH  Google Scholar 

  31. Geers M, De Borst R, Brekelmans W, Peerlings R (1998) Strain-based transient-gradient damage model for failure analyses. Comput Methods Appl Mech Eng 160(1):133–153

    MATH  Google Scholar 

  32. Geertsma J, De Klerk F et al (1969) A rapid method of predicting width and extent of hydraulically induced fractures. J Pet Technol 21(12):1–571

    Google Scholar 

  33. Gordeliy E, Peirce A (2013) Coupling schemes for modeling hydraulic fracture propagation using the xfem. Comput Methods Appl Mech Eng 253:305–322

    MathSciNet  MATH  Google Scholar 

  34. Gordeliy E, Peirce A (2013) Implicit level set schemes for modeling hydraulic fractures using the xfem. Comput Methods Appl Mech Eng 266:125–143

    MathSciNet  MATH  Google Scholar 

  35. Gordeliy E, Peirce A (2015) Enrichment strategies and convergence properties of the xfem for hydraulic fracture problems. Comput Methods Appl Mech Eng 283:474–502

    MathSciNet  MATH  Google Scholar 

  36. Green A, Sneddon I (1950) The distribution of stress in the neighbourhood of a flat elliptical crack in an elastic solid. In: Mathematical Proceedings of the Cambridge Philosophical Society, vol 46. Cambridge University Press, pp. 159–163

  37. Gupta P, Duarte CA (2014) Simulation of non-planar three-dimensional hydraulic fracture propagation. Int J Numer Anal Methods Geomech 38(13):1397–1430

    Google Scholar 

  38. Hu J, Garagash DI (2010) Plane-strain propagation of a fluid-driven crack in a permeable rock with fracture toughness. J Eng Mech 136(9):1152–1166

    Google Scholar 

  39. Jin W (2018) Computational modeling of the transition from damage to fracture in intrinsically anisotropic porous media. Ph.D. thesis, Georgia Institute of Technology

  40. Jin W, Arson C (2017) Modeling of tensile and compressive damage in layered sedimentary rock: a direction dependent non-local model. In: 51st US Rock Mechanics/Geomechanics Symposium. American Rock Mechanics Association

  41. Jin W, Arson C (2018) Anisotropic nonlocal damage model for materials with intrinsic transverse isotropy. Int J Solids Struct 139:29–42

    Google Scholar 

  42. Jin W, Arson C (2019) Xfem to couple nonlocal micromechanics damage with discrete mode i cohesive fracture. Comput Methods Appl Mech Eng (under review)

  43. Jirasek M (1998) Nonlocal models for damage and fracture: comparison of approaches. Int J Solids Struct 35(31):4133–4145

    MathSciNet  MATH  Google Scholar 

  44. Jirásek M, Patzák B (2002) Consistent tangent stiffness for nonlocal damage models. Comput Struct 80(14):1279–1293

    Google Scholar 

  45. Jirasek M, Zimmermann T (2001) Embedded crack model. Part II: combination with smeared cracks. Int J Numer Methods Eng 50(6):1291–1305

    MATH  Google Scholar 

  46. Khoei A, Vahab M, Hirmand M (2016) Modeling the interaction between fluid-driven fracture and natural fault using an enriched-fem technique. Int J Fract 197(1):1–24

    Google Scholar 

  47. Khoei A, Vahab M, Hirmand M (2018) An enriched-fem technique for numerical simulation of interacting discontinuities in naturally fractured porous media. Comput Methods Appl Mech Eng 331:197–231

    MathSciNet  Google Scholar 

  48. Khoei AR, Hirmand M, Vahab M, Bazargan M (2015) An enriched fem technique for modeling hydraulically driven cohesive fracture propagation in impermeable media with frictional natural faults: Numerical and experimental investigations. Int J Numer Methods Eng 104(6):439–468

    MathSciNet  MATH  Google Scholar 

  49. Khoei AR, Vahab M, Haghighat E, Moallemi S (2014) A mesh-independent finite element formulation for modeling crack growth in saturated porous media based on an enriched-fem technique. Int J Fract 188(1):79–108

    Google Scholar 

  50. Khristianovic S, Zheltov Y (1955) Formation of vertical fractures by means of highly viscous fluids. In: Proceedings of 4th world petroleum congress, Rome, vol 2, pp 579–586

  51. Kresse O, Weng X, Gu H, Wu R (2013) Numerical modeling of hydraulic fractures interaction in complex naturally fractured formations. Rock Mech Rock Eng 46(3):555–568

    Google Scholar 

  52. Leclerc J, Wu L, Nguyen VD, Noels L (2018) A damage to crack transition model accounting for stress triaxiality formulated in a hybrid nonlocal implicit discontinuous galerkin-cohesive band model framework. Int J Numer Methods Eng 113(3):374–410

    MathSciNet  Google Scholar 

  53. Lenoach B (1995) The crack tip solution for hydraulic fracturing in a permeable solid. J Mech Phys Solids 43(7):1025–1043

    MATH  Google Scholar 

  54. Li C, Caner FC, Chau VT, Bažant ZP (2017) Spherocylindrical microplane constitutive model for shale and other anisotropic rocks. J Mech Phys Solids 103:155–178

    MathSciNet  Google Scholar 

  55. McLennan JD, Picardy JC et al (1985) Pseudo-three-dimensional fracture growth modeling. In: The 26th US Symposium on Rock Mechanics (USRMS). American Rock Mechanics Association

  56. Miehe C, Mauthe S, Teichtmeister S (2015) Minimization principles for the coupled problem of darcy-biot-type fluid transport in porous media linked to phase field modeling of fracture. J Mech Phys Solids 82:186–217

    MathSciNet  Google Scholar 

  57. Mohammadnejad T, Andrade J (2016) Numerical modeling of hydraulic fracture propagation, closure and reopening using xfem with application to in-situ stress estimation. Int J Numer Anal Methods Geomech 40(15):2033–2060

    Google Scholar 

  58. Mohammadnejad T, Khoei A (2013) An extended finite element method for fluid flow in partially saturated porous media with weak discontinuities; the convergence analysis of local enrichment strategies. Comput Mech 51(3):327–345

    MathSciNet  MATH  Google Scholar 

  59. Mohammadnejad T, Khoei A (2013) An extended finite element method for hydraulic fracture propagation in deformable porous media with the cohesive crack model. Finite Elements Anal Des 73:77–95

    MathSciNet  MATH  Google Scholar 

  60. Nordgren R et al (1972) Propagation of a vertical hydraulic fracture. Soc Pet Eng J 12(04):306–314

    Google Scholar 

  61. Palmer I, Carroll Jr H et al (1983) Numerical solution for height and elongated hydraulic fractures. In: SPE/DOE Low Permeability Gas Reservoirs Symposium. Society of Petroleum Engineers

  62. Park K, Choi H, Paulino GH (2016) Assessment of cohesive traction-separation relationships in abaqus: a comparative study. Mech Res Commun 78:71–78

    Google Scholar 

  63. Park K, Paulino GH (2011) Cohesive zone models: a critical review of traction-separation relationships across fracture surfaces. Appl Mech Rev 64(6):060802

    Google Scholar 

  64. Park K, Paulino GH (2012) Computational implementation of the ppr potential-based cohesive model in abaqus: educational perspective. Eng Fract Mech 93:239–262

    Google Scholar 

  65. Park K, Paulino GH, Roesler JR (2009) A unified potential-based cohesive model of mixed-mode fracture. J Mech Phys Solids 57(6):891–908

    Google Scholar 

  66. Peirce A (2015) Modeling multi-scale processes in hydraulic fracture propagation using the implicit level set algorithm. Comput Methods Appl Mech Eng 283:881–908

    MathSciNet  MATH  Google Scholar 

  67. Peirce A, Detournay E (2008) An implicit level set method for modeling hydraulically driven fractures. Comput Methods Appl Mech Eng 197(33–40):2858–2885

    MATH  Google Scholar 

  68. Perkins T, Kern L et al (1961) Widths of hydraulic fractures. J Pet Technol 13(09):937–949

    Google Scholar 

  69. Remij E, Remmers J, Huyghe J, Smeulders D (2015) The enhanced local pressure model for the accurate analysis of fluid pressure driven fracture in porous materials. Comput Methods Appl Mech Eng 286:293–312

    MathSciNet  MATH  Google Scholar 

  70. Roth SN, Léger P, Soulaïmani A (2015) A combined xfem-damage mechanics approach for concrete crack propagation. Comput Methods Appl Mech Eng 283:923–955

    MathSciNet  MATH  Google Scholar 

  71. Salimzadeh S, Khalili N (2015) A three-phase xfem model for hydraulic fracturing with cohesive crack propagation. Comput Geotech 69:82–92

    Google Scholar 

  72. Savitski A, Detournay E (2002) Propagation of a penny-shaped fluid-driven fracture in an impermeable rock: asymptotic solutions. Int J Solids Struct 39(26):6311–6337

    MATH  Google Scholar 

  73. Semnani SJ, White JA, Borja RI (2016) Thermoplasticity and strain localization in transversely isotropic materials based on anisotropic critical state plasticity. Int J Numer Anal Methods Geomech 40(18):2423–2449

    Google Scholar 

  74. Settari A, Cleary MP et al (1986) Development and testing of a pseudo-three-dimensional model of hydraulic fracture geometry. SPE Prod Eng 1(06):449–466

    Google Scholar 

  75. Siebrits E, Peirce AP (2002) An efficient multi-layer planar 3d fracture growth algorithm using a fixed mesh approach. Int J Numer Methods Eng 53(3):691–717

    MATH  Google Scholar 

  76. Simone A, Askes H, Sluys LJ (2004) Incorrect initiation and propagation of failure in non-local and gradient-enhanced media. Int J Solids Struct 41(2):351–363

    MATH  Google Scholar 

  77. Simone A, Wells GN, Sluys LJ (2003) From continuous to discontinuous failure in a gradient-enhanced continuum damage model. Comput Methods Appl Mech Eng 192(41):4581–4607

    MATH  Google Scholar 

  78. Sneddon IN (1946) The distribution of stress in the neighbourhood of a crack in an elastic solid. Proc R Soc Lond A 187(1009):229–260

    MathSciNet  Google Scholar 

  79. Song SH, Paulino GH, Buttlar WG (2006) A bilinear cohesive zone model tailored for fracture of asphalt concrete considering viscoelastic bulk material. Eng Fract Mech 73(18):2829–2848

    Google Scholar 

  80. Spence DA, Sharp P (1985) Self-similar solutions for elastohydrodynamic cavity flow. Proc R Soc Lond A 400(1819):289–313

    MathSciNet  MATH  Google Scholar 

  81. Tien YM, Kuo MC (2001) A failure criterion for transversely isotropic rocks. Int J Rock Mech Mining Sci 38(3):399–412

    Google Scholar 

  82. Turon A, Davila CG, Camanho PP, Costa J (2007) An engineering solution for mesh size effects in the simulation of delamination using cohesive zone models. Eng Fract Mech 74(10):1665–1682

    Google Scholar 

  83. Vahab M, Khalili N (2018) X-fem modeling of multizone hydraulic fracturing treatments within saturated porous media. Rock Mech Rock Eng 51:3219–3239

    Google Scholar 

  84. Vandamme L, Curran JH (1989) A three-dimensional hydraulic fracturing simulator. Int J Numer Methods Eng 28(4):909–927

    Google Scholar 

  85. Wang Y, Waisman H (2016) From diffuse damage to sharp cohesive cracks: a coupled xfem framework for failure analysis of quasi-brittle materials. Comput Methods Appl Mech Eng 299:57–89

    MathSciNet  MATH  Google Scholar 

  86. Wells G, Sluys L, De Borst R (2002) Simulating the propagation of displacement discontinuities in a regularized strain-softening medium. Int J Numer Methods Eng 53(5):1235–1256

    Google Scholar 

  87. Zienkiewicz OC, Zhu JZ (1992) The superconvergent patch recovery and a posteriori error estimates. Part 1: the recovery technique. Int J Numer Methods Eng 33(7):1331–1364

    MATH  Google Scholar 

Download references

Acknowledgements

Financial support for this research was provided by the U.S. National Science Foundation, under Grant 1552368: “CAREER: Multiphysics Damage and Healing of Rocks for Performance Enhancement of Geo-Storage Systems—A Bottom–Up Research and Education Approach”

Author information

Authors and Affiliations

  1. Energy and Environment Science & Technology Directorate, Idaho National Laboratory, Idaho Falls, ID, USA

    Wencheng Jin

  2. School of Civil and Environmental Engineering, Georgia Institute of Technology, Atlanta, GA, USA

    Chloé Arson

Authors
  1. Wencheng Jin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chloé Arson
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chloé Arson.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jin, W., Arson, C. Fluid-driven transition from damage to fracture in anisotropic porous media: a multi-scale XFEM approach. Acta Geotech. 15, 113–144 (2020). https://doi.org/10.1007/s11440-019-00813-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11440-019-00813-x

Keywords

Search

Navigation