Skip to main content
SpringerLink
Log in

Analytical derivation of water retention for random monodisperse granular media

  • Research Paper
  • Published:
Acta Geotechnica Aims and scope Submit manuscript

Abstract

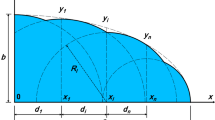
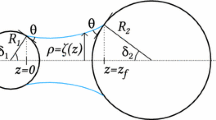
The mechanics of water retention in unsaturated granular media is of critical importance to a broad range of disciplines including soil science, geotechnical engineering, hydrology and agriculture. Fundamental to water retention is the relationship between degree of saturation and suction, referred to as the water retention curve (WRC). The majority of WRC models are empirically based and seldom incorporate physically meaningful parameters. This study presents an analytical model for the WRC that considers separate contributions from fully filled pores and partially filled pores containing liquid bridges. A recently established unique k-gamma pore volume distribution function for randomly assembled monodisperse granular materials is adopted to determine the contributions of fully filled pores. Calculation of the contribution of residual pore water retained in partially filled pores is undertaken by representing pores as individual cells shaped as platonic shapes of various sizes and determining the volume of all liquid bridges suspended between particles within the pore cells. Weighting factors for the various cell types are obtained from the pore volume distribution to determine the relative contribution of different pore cell geometries to the total residual pore water. The combined model accurately describes experimental data for monodisperse spherical glass beads for both wetting and drying, even though the underlying assumptions do not reflect exactly the complex, interconnected and highly irregular geometry of the pore space. A single parameter provides the lateral shift between the wetting and drying curves. The results of this study provide a geometric understanding of the mechanisms of water retention in granular media.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Aste T, Di Matteo T (2008) Emergence of Gamma distributions in granular materials and packing models. Phys Rev E 77(2):021309

    Article  Google Scholar 

  2. Aste T, Di Matteo T, Saadatfar M, Senden TJ, Schröter M, Swinney HL (2007) An invariant distribution in static granular media. Europhys Lett 79(2):24003

    Article  Google Scholar 

  3. Beckett CTS, Augarde CE (2013) Prediction of soil water retention properties using pore-size distribution and porosity. Can Geotech J 50(4):435–450

    Article  Google Scholar 

  4. Bird NRA, Perrier E, Rieu M (2000) The water retention function for a model of soil structure with pore and solid fractal distributions. Eur J Soil Sci 51(1):55–63

    Article  Google Scholar 

  5. Birle E, Heyer D, Vogt N (2008) Influence of the initial water content and dry density on the soil-water retention curve and the shrinkage behaviour of a compacted clay. Acta Geotech 3:191–200

    Article  Google Scholar 

  6. Blonquist JM, Jones SB, Lebron I, Robinson D (2006) Microstructural and phase configurational effects determining water content: dielectric relationships of aggregated porous media. Water Resour Res 42(5):1–13

    Article  Google Scholar 

  7. Brooks RH, Corey AT (1964) Hydraulic properties of porous media. Hydrology Paper No. 3, Civil Engineering Department, Colorado State University, Fort Collins, Colorado

  8. Casini F, Vaunat J, Romero E, Desideri A (2012) Consequences on water retention properties of double-porosity features in a compacted silt. Acta Geotech 7:139–150

    Article  Google Scholar 

  9. Della Vecchia G, Dieudonné A-C, Jommi C, Charlier R (2015) Accounting for evolving pore size distribution in water retention models for compacted clays. Int J Numer Anal Meth Geomech 39:702–723

    Article  Google Scholar 

  10. Dury O, Fischer U, Schulin R (1998) Dependence of hydraulic and pneumatic characteristics of soils on a dissolved organic compound. J Contam Hydrol 33(1–2):39–57

    Article  Google Scholar 

  11. Finney JL (1970) Random packings and the structure of simple liquids. I. The geometry of random close packing. Proc R Soc Lond 319:479–493

    Article  Google Scholar 

  12. Fredlund DG, Sheng D, Zhao J (2011) Estimation of soil suction from the soil-water characteristic curve. Can Geotech J 48:186–198

    Article  Google Scholar 

  13. Fredlund DG, Xing A (1994) Equations for the soil-water characteristic curve. Can J Geotechn Eng 31:521–532

    Article  Google Scholar 

  14. Gimenez D, Perfect E, Rawls WJ, Packepsky Y (1997) Fractal models for predicting soil hydraulic properties: a review. J Eng Geol 48(3–4):161–183

    Article  Google Scholar 

  15. Haines WB (1930) Studies in the physical properties of soil. V. The hysteresis effect in capillary properties and the modes of moisture distribution associated therewith. J Agric Sci 20(1):97–116

    Article  Google Scholar 

  16. Hu R, Chen YF, Liu HH, Zhon CB (2013) A water retention curve and unsaturated hydraulic conductivity model for deformable soils: consideration of the change in pore-size distribution. Géotechnique 63(16):1389–1405

    Article  Google Scholar 

  17. Kasangaki GJ, Medero GM, Ooi JY (2012) Factors influencing water retention characteristics of granular materials. In: Laloui L, Ferrari A (eds) Multiphysical testing of soils and shales. Springer, Berlin, pp 111–116

    Google Scholar 

  18. Khalili N, Habte MA, Zargarbashi S (2008) A fully coupled flow deformation model for cyclic analysis of unsaturated soils including hydraulic and mechanical hysteresis. Comput Geotech 35(6):872–889

    Article  Google Scholar 

  19. Klein T et al (2014) Quantifying transpirable soil water and its relations to tree water use dynamics in a water-limited pine forest. Ecohydrology 7(2):409–419

    Article  Google Scholar 

  20. Laloui L, Salager S, Rizzi M (2013) Retention behaviour of natural clayey materials at different temperatures. Acta Geotech 2013:537–546

    Article  Google Scholar 

  21. Likos WJ (2009) Pore-Scale model for water retention in unsaturated sand. In: AIP conference proceedings, vol 1145, pp 907–910

  22. Likos WJ, Jaafar R (2013) Pore-scale model for water retention and fluid partitioning of partially saturated granular soil. J Geotech Geoenviron Eng 139:724–737

    Article  Google Scholar 

  23. Mah K-C, Tan Y-C, Chem C-H (2011) The influence of water retention curve hysteresis on the stability of unsaturated soil slopes. Hydrol Process 25:3563–3574

    Article  Google Scholar 

  24. Megias-Alguacil D, Gauckler JL (2009) Capillary forces between two solid spheres linked by a concave liquid bridge: regions of existence and forces mapping. Wiley InterScience, Zurich

    Google Scholar 

  25. Millington RJ, Quirk JP (1959) Permeability of porous media. Nature 183:387–388

    Article  Google Scholar 

  26. Mualem Y (1976) A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour Res 12(3):513–522

    Article  Google Scholar 

  27. Nimmo JR (2004) Porosity and pore size distribution. In: Hillel D (ed) Encyclopedia of soils in the environment. Elsevier, London, pp 295–393

    Google Scholar 

  28. Nimmo JR, Miller EE (1986) The temperature dependence of isothermal moisture vs potential characteristics of soil. Soil Sci Soc Am 50:1105–1113

    Article  Google Scholar 

  29. Or D, Tuller M (1999) Liquid retention and interfacial area in variably saturated porous media: upscaling from single-pore to sample-scale model. Water Resour Res 32(12):3591–3605

    Article  Google Scholar 

  30. Russell AR (2010) Water retention characteristics of double porosity soils. Eur J Soil Sci 61(3):412–424

    Article  Google Scholar 

  31. Russell AR, Buzzi O (2012) A fractal basis for soil water characteristic curves with hydraulic hysteresis. Géotechnique 62(3):269–274

    Article  Google Scholar 

  32. Russell AR (2014) How water retention in fractal soils depends on particle and pore sizes, shapes, volumes and surface areas. Geotechnique 64(5):379–390

    Article  Google Scholar 

  33. Sufian A, Russell A, Whittle A, Saadatfar M (2015) Pore shapes, volume distribution and orientations in monodisperse granular assemblies. Granul Matter 17(6):1–16

    Article  Google Scholar 

  34. To HD, Scheuermann A, Williams DJ (2012) A new simple model for the determination of the pore constriction size distribution. In: International conference on scour and erosion, Paris

  35. van Genuchten MT (1980) A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci Soc Am J 44(5):892–898

    Article  Google Scholar 

  36. Vincens E, Witt KJ, Homberg U (2015) Approaches to determine the constriction size distribution for understanding filtration phenomena in granular materials. Acta Geotech 10(3):291–303

    Article  Google Scholar 

  37. Wang X, Li J (2015) A novel liquid bridge model for estimating SWCC and permeability of granular material. Powder Technol 275:121–130

    Article  Google Scholar 

  38. Yang H, Khoshgalb A, Russell AR (2014) Fractal-based estimation of hydraulic conductivity from soil-water characteristic curves considering hysteresis. Goetech Lett 4:1–10

    Google Scholar 

Download references

Acknowledgements

Thanks go to the Australian Research Council for funding through Grant DP150104123.

Author information

Authors and Affiliations

  1. Centre for Infrastructure Engineering and Safety, School of Civil and Environmental Engineering, The University of New South Wales, Sydney, NSW, 2052, Australia

    Anthony Ferraro, Adnan Sufian & Adrian R. Russell

Authors
  1. Anthony Ferraro
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Adnan Sufian
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Adrian R. Russell
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Adrian R. Russell.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ferraro, A., Sufian, A. & Russell, A.R. Analytical derivation of water retention for random monodisperse granular media. Acta Geotech. 12, 1319–1328 (2017). https://doi.org/10.1007/s11440-017-0546-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11440-017-0546-0

Keywords

Search

Navigation