A simple hypoplastic model for normally consolidated clay

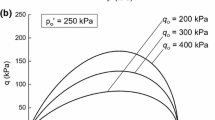
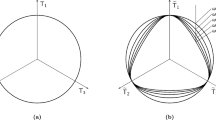
Abstract

The paper presents a simple constitutive model for normally consolidated clay. A mathematical formulation, using a single tensor-valued function to define the incrementally nonlinear stress–strain relation, is proposed based on the basic concept of hypoplasticity. The structure of the tensor-valued function is determined in the light of the response envelope. Particular attention is paid towards incorporating the critical state and to the capability for capturing undrained behaviour of clayey soils. With five material parameters that can be determined easily from isotropic consolidation and triaxial compression tests, the model is shown to provide good predictions for the response of normally consolidated clay along various stress paths, including drained true triaxial tests and undrained shear tests.

Appendix

Here we present a brief description of the hypoplastic model proposed by Mašín [12]. The constitutive equation is

$$\dot{\varvec{\sigma} } = f_{\rm s} \,{\mathbf {L}}:\dot{\varvec{\varepsilon} } + f_{\rm s} f_{\rm d} {\user2{N}}\left\|\dot{\varvec{\varepsilon} }\right\|\,.$$

Here the fourth order tensor L takes the form

$$\,{\mathbf {L}}\, = 3(c_{1} \,{\mathbf {I}}\, + c_{2}a^{2} \hat{\varvec{\sigma} } \otimes \hat{\varvec{\sigma} }),$$

and the second order tensor N is given as

$${\user2 {N}} = {\mathbf {L}}:\left(- Y\frac{{\user2 {m}}}{{\left\|{\user2 {m}}\right\|}}\right),$$

with m being defined by

$${\user2 {m}} = - \frac{a}{F}{\left[ {\frac{{(F/a)^{2} - \hat{\varvec{\sigma} }_{\rm d}:\hat{\varvec{\sigma} }_{\rm d} }}{{(F/a)^{2} + \hat{\varvec{\sigma} }:\hat{\varvec{\sigma} }}}\hat{\varvec{\sigma} } + \hat{\varvec{\sigma} }_{\rm d} } \right]}.$$

In these equations, the parameters a and F are related to the critical friction angle φ_c and the Lode angle θ through the relation [21]

$$a = \frac{{{\sqrt 3 }\,(3 - \sin\,\varphi_{\rm c})}}{{2{\sqrt 2 }\,\sin\,\varphi_{\rm c} }},\quad F = {\sqrt {\frac{1}{8}\tan ^{2} \psi + \frac{{2 - \tan ^{2} \psi }}{{2 + {\sqrt 2 }\tan \psi \cos (3\theta)}}} } - \frac{1}{{2{\sqrt 2 }}}\tan \psi$$

with $\tan \psi = {\sqrt 3 }|\hat{\varvec{\sigma} }_{\rm d} \,|.$ The parameter Y in expression for N, known as the degree of nonlinearity [16], has the following form:

$$Y = {\left({\frac{{{\sqrt 3 }a}}{{3 + a^{2} }} - 1} \right)}\frac{{(I_{1} I_{2} + 9I_{3})(1 - \sin ^{2} \varphi_{\rm c})}}{{8I_{3} \sin ^{2} \varphi_{\rm c} }} + \frac{{{\sqrt 3 }a}}{{3 + a^{2} }},$$

where I ₁, I ₂ and I ₃ are the first, second and third stress invariants, respectively:

$$I_{1} = \operatorname{tr} \varvec{\sigma}, \quad I_{2} = \frac{1}{2}[\varvec{\sigma}:\varvec{\sigma} - (I_{1})^{2} ]\,,\quad I_{3} = \det \varvec{\sigma}.$$

The factors f _s and f _d in Eq. 29 are defined by

$$f_{\rm s} = - \frac{{\operatorname{tr} \varvec{\sigma} }}{{\lambda^{*} }}(3 + a^{2} - 2^{\alpha } a{\sqrt 3 })^{{ - 1}}, \quad f_{\rm d} = {\left[ { - \frac{1}{2}\operatorname{tr} \varvec{\sigma} \exp {\left({\frac{{\log (1 + e) - N^{*} }}{{\lambda ^{*} }}} \right)}} \right]}^{\alpha },$$

where the scalar parameter α can be determined from

$$\alpha = \frac{1}{{\ln 2}}\ln {\left[ {\frac{{\lambda ^{*} - \kappa ^{*} }}{{\lambda ^{*} + \kappa ^{*} }}\frac{{3 + a}}{{{\sqrt 3 }a}}} \right]}.$$

The factors c ₁ and c ₂ in above equation are related to other parameters via

$$c_{1} = \frac{{2(3 + a^{2} - 2^{\alpha } a{\sqrt 3 })}}{{9r}}\,,\quad c_{2} = 1 + (1 - c_{1})\frac{3}{{a^{2} }}.$$

The model contains five parameters: φ_c, λ^*, κ^*, r and N ^*, where φ_c is the critical state friction angle, λ^* and κ^* has the same meaning as in Eq.10a, b, r is the ratio of the bulk modulus over the shear modulus at an isotropic stress state, r=K ⁺ _i /G _i , and N ^* represents the logarithmic specific volume at a mean pressure of 1 kPa so that N ^*=ln (1+e) |_p=1 kPa.