Abstract
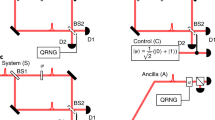
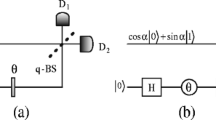
In this paper, a realistic interpretation (REIN) of the wave function in quantum mechanics is briefly presented. We demonstrate that in the REIN, the wave function of a microscopic object is its real existence rather than a mere mathematical description. Specifically, the quantum object can exist in disjointed regions of space just as the wave function is distributed, travels at a finite speed, and collapses instantly upon a measurement. Furthermore, we analyze the single-photon interference in a Mach-Zehnder interferometer (MZI) using the REIN. Based on this, we propose and experimentally implement a generalized delayed-choice experiment, called the encounter-delayed-choice experiment, where the second beam splitter is decided whether or not to insert at the encounter of two sub-waves along the arms of the MZI. In such an experiment, the parts of the sub-waves, which do not travel through the beam splitter, show a particle nature, whereas the remaining parts interfere and thus show a wave nature. The predicted phenomenon is clearly demonstrated in the experiment, thus supporting the REIN idea.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Change history
20 March 2018
The article Realistic interpretation of quantum mechanics and encounter-delayed-choice experiment, written by GuiLu Long, Wei Qin, Zhe Yang, and Jun-Lin Li, was originally published online without open access. After publication in volume 61, issue 3: 030311 the author decided to opt for Open Choice and to make the article an open access publication. Therefore, the copyright of the article has been changed to © The Author(s) 2017 and the article is forthwith distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
The original article has been corrected.
References
K. F. Weizsäcker, Z. Phys. 70, 114 (1931).
C. F. von Weizsäcker, Z. Phys. 118, 489 (1941).
J. A. Wheeler, in: Mathematical Foundations of Quantum Theory, edited by A. R. Marlow (Academic Press, Cambridge, 1978), pp. 9–48.
T. Hellmuth, H. Walther, A. Zajonc, and W. Schleich, Phys. Rev. A 35, 2532 (1987).
B. J. Lawson-Daku, R. Asimov, O. Gorceix, C. Miniatura, J. Robert, and J. Baudon, Phys. Rev. A 54, 5042 (1996).
Y. H. Kim, R. Yu, S. P. Kulik, Y. Shih, and M. O. Scully, Phys. Rev. Lett. 84, 1 (2000).
V. Jacques, E. Wu, F. Grosshans, F. Treussart, P. Grangier, A. Aspect, and J. F. Roch, Science 315, 966 (2007).
V. Jacques, E. Wu, F. Grosshans, F. Treussart, P. Grangier, A. Aspect, and J. F. Roch, Phys. Rev. Lett. 100, 220402 (2008).
X. Ma, S. Zotter, J. Kofler, R. Ursin, T. Jennewein, Brukner, and A. Zeilinger, Nat. Phys. 8, 480 (2012).
R. Ionicioiu, and D. R. Terno, Phys. Rev. Lett. 107, 230406 (2011).
M. Schirber, Physics 4, 102 (2011).
S. S. Roy, A. Shukla, and T. S. Mahesh, Phys. Rev. A 85, 022109 (2012).
R. Auccaise, R. M. Serra, J. G. Filgueiras, R. S. Sarthour, I. S. Oliveira, and L. C. Céleri, Phys. Rev. A 85, 032121 (2012).
A. Peruzzo, P. Shadbolt, N. Brunner, S. Popescu, and J. L. OBrien, Science 338, 634 (2012).
F. Kaiser, T. Coudreau, P. Milman, D. B. Ostrowsky, and S. Tanzilli, Science 338, 637 (2012).
J. S. Tang, Y. L. Li, X. Y. Xu, G. Y. Xiang, C. F. Li, and G. C. Guo, Nat. Photon. 6, 602 (2012).
G. Adesso, and D. Girolami, Nat. Photon. 6, 579 (2012).
L. C. Céleri, R. M. Gomes, R. Ionicioiu, T. Jennewein, R. B. Mann, and D. R. Terno, Found. Phys. 44, 576 (2014).
R. Ionicioiu, T. Jennewein, R. B. Mann, and D. R. Terno, Nat. Commun. 5, 3997 (2014).
J. S. Lundeen, B. Sutherland, A. Patel, C. Stewart, and C. Bamber, Nature 474, 188 (2011).
S. Kocsis, B. Braverman, S. Ravets, M. J. Stevens, R. P. Mirin, L. K. Shalm, and A. M. Steinberg, Science 332, 1170 (2011).
W. P. Schleich, M. Freyberger, and M. S. Zubairy, Phys. Rev. A 87, 014102 (2013).
L. D. Landau, and E. M. Lifshitz, Quantum Mechanics: Non-Relativistic Theory in Course of Theoretical Physics Vol. 3, 3rd ed, (Pergamon Press, Oxford, 1989), p. 6.
C. Cohen-Tannoudji, B. Diu, and F. Laloe, Quantum Mechanics Vol. 1 (Wiley-Interscience, New York, 2006), p. 19.
N. D. Mermin, Phys. Today 62, 8 (2009).
G. L. Long, Sci. Bull. 62, 1355 (2017).
G. L. Long, Commun. Theor. Phys. 45, 825 (2006).
G. L. Long, and L. Yang, Commun. Theor. Phys. 50, 1303 (2008).
G. L. Long, L. Yang, and W. Chuan, Commun. Theor. Phys. 51, 65 (2009).
S. Gudder, Quant. Inf. Process. 6, 37 (2007).
G. L. Long, Quant. Inf. Process. 6, 49 (2007).
G. L. Long, and L. Yang, Commun. Theor. Phys. 50, 1303 (2008).
G. L. Long, Int. J. Theor. Phys. 50, 1305 (2011).
C. Y. Li, W. Y. Wang, C. Wang, S.Y. Song, and G. L. Long, in: Duality Quantum Information and Duality Quantum Communication: Proceedings of the International Conference on Advances in Quantum Theory, edited by G. Jaeger, A. Khrennikov, M. Schlosshauer, and G. Weihs (AIP Publishing, Växjö, 2011) pp. 158–165.
A. M. Childs, and N. Wiebe, arXiv: 1202.5822.
Z. Y. Zhou, Z. H. Zhu, S. L. Liu, Y. H. Li, S. Shi, D. S. Ding, L. X. Chen, W. Gao, G. C. Guo, and B. S. Shi, Sci. Bull. 62, 1185 (2017).
D. W. Berry, A. M. Childs, R. Cleve, R. Kothari, and R. D. Somma, Phys. Rev. Lett. 114, 090502 (2015).
S. J. Wei, and G. L. Long, Quant. Inf. Process. 15, 1189 (2016).
S. J. Wei, D. Ruan, and G. L. Long, Sci. Rep. 6, 30727 (2016).
A. W. Harrow, A. Hassidim, and S. Lloyd, Phys. Rev. Lett. 103, 150502 (2009).
S. J. Wei, Z. R. Zou, D. Ruan, and G. L. Long, in Realization of the Algorithm for System of Linear Equations in Duality Quantum Computing: Proceeding of IEEE 85th Vehicular Technology Conference (Spring, Sydney, 2017).
X. Qiang, X. Zhou, K. Aungskunsiri, H. Cable, and J. L. OBrien, Quant. Sci. Technol. 2, 045002 (2017).
R. J. Marshman, A. P. Lund, P. P. Rohde, and T. C. Ralph, arXiv: 1709.02157.
Author information
Authors and Affiliations
Corresponding author
Additional information
The original version of this article was revised due to a retrospective Open Access order.
A correction to this article is available at https://doi.org/10.1007/s11433-018-9198-0
An erratum to this article is available at https://doi.org/10.1007/s11433-018-9198-0.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
About this article
Cite this article
Long, G., Qin, W., Yang, Z. et al. Realistic interpretation of quantum mechanics and encounter-delayed-choice experiment. Sci. China Phys. Mech. Astron. 61, 030311 (2018). https://doi.org/10.1007/s11433-017-9122-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11433-017-9122-2