Skip to main content
SpringerLink
Log in

The refined theory of deep rectangular beams based on general solutions of elasticity

  • Published:
Science in China Series G Aims and scope Submit manuscript

Abstract

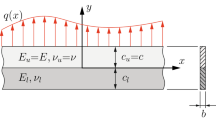
The problem of deducing one-dimensional theory from two-dimensional theory for a homogeneous isotropic beam is investigated. Based on elasticity theory, the refined theory of rectangular beams is derived by using Papkovich-Neuber solution and Lur’e method without ad hoc assumptions. It is shown that the displacements and stresses of the beam can be represented by the angle of rotation and the deflection of the neutral surface. Based on the refined beam theory, the exact equations for the beam without transverse surface loadings are derived and consist of two governing differential equations: the fourth-order equation and the transcendental equation. The approximate equations for the beam under transverse loadings are derived directly from the refined beam theory and are almost the same as the governing equations of Timoshenko beam theory. In two examples, it is shown that the new theory provides better results than Levinson’s beam theory when compared with those obtained from the linear theory of elasticity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Timoshenko S P. On the correction for shear of the differential equation for transverse vibration of prismatic bars. Phi Mag, 1921, 41: 744–746

    Google Scholar 

  2. Cowper G R. The shear coefficients in Timoshenko’s beam theory. J Appl Mech, 1966, 33: 335–340

    MATH  Google Scholar 

  3. Levinson M. A new rectangular beam theory. J Sound Vib, 1981, 74(1): 81–87

    Article  MATH  ADS  Google Scholar 

  4. Bickford W B. A consistent higher order beam theory. Developments in Theoretical and Appl Mech, 1982, 11: 137–150

    Google Scholar 

  5. Tutek Z, Aganović I. A justification of the one-dimensional linear model of elastic beam. Math Meth Appl Sci, 1986, 8: 502–515

    MATH  Google Scholar 

  6. Lewiński T. On the twelfth-order theory of elastic plates. Mech Res Commun, 1990, 17(6): 375–382

    Article  MATH  Google Scholar 

  7. Fan H, Widera G E O. Refined engineering beam theory based on the asymptotic expansion approach. AIAA J, 1992, 29(3): 444–449

    Article  ADS  Google Scholar 

  8. Tullini N, Savoia M. Elasticity interior solution for orthotropic strips and the accuracy of beam theories. J Appl Mech, 1999, 66(2): 368–373

    MathSciNet  Google Scholar 

  9. Cheng S. Elasticity theory of plates and a refined theory. J Appl Mech, 1979, 46(2): 644–650

    MATH  Google Scholar 

  10. Lur’e A I. Three-Dimensional Problems of the Theory of Elasticity. New York: Interscience, 1964

    MATH  Google Scholar 

  11. Barrett K E, Ellis S. An exact theory of elastic plates. Int J Solids Struct, 1988, 24: 859–880

    Article  MathSciNet  MATH  Google Scholar 

  12. Gregory R D, Wan F Y M. Decaying states of plane strain in a semi-infinite strip and boundary conditions for plate theory. J Elast, 1984, 14: 27–64

    Article  MathSciNet  MATH  Google Scholar 

  13. Gregory R D, Wan F Y M. On plate theories and Saint-Venant’s principle. Int J Solids Struct, 1985, 21: 1005–1024

    Article  MathSciNet  MATH  Google Scholar 

  14. Wang W, Shi M X. Thick plate theory based on general solutions of elasticity. Acta Mech, 1997, 123: 27–36

    Article  MathSciNet  MATH  Google Scholar 

  15. Yin H M, Wang W. A refined theory of transversely isotropic plates. Acta Sci Natur Univ Pek, 2001, 37(1): 23–33

    MathSciNet  MATH  Google Scholar 

  16. Xu S P, Wang W. A refined theory of transversely isotropic piezoelectric plates. Acta Mech, 2004, 171: 15–27

    Article  MATH  Google Scholar 

  17. Gao Y, Wang M Z. The refined theory of magnetoelastic rectangular beams. Acta Mech, 2004, 173(1–4): 147–161

    Article  MathSciNet  MATH  Google Scholar 

  18. Gao Y, Wang M Z. A refined theory of thermoelastic beams under steady temperature. Eng Mech, 2006, 23(2):34–40

    MathSciNet  Google Scholar 

  19. Dym C L, Shames I H. Solid Mechanics: A Variational Approach. New York: McGraw-Hill, 1973

    Google Scholar 

  20. Wang M Z, Xu X S. A generalization of Almansi’s theorem and its application. App Math Modell, 1990, 14: 275–279

    Article  MathSciNet  MATH  Google Scholar 

  21. Wang W, Wang M Z. On single-valuedness of the Papkovich-Neuber solution in two-dimensional elasticity. Mech Res Commun, 1990, 17: 403–408

    Article  ADS  MATH  Google Scholar 

  22. Wang W, Wang M Z. Constructivity and completeness of the general solutions in elastodynamics. Acta Mechanica, 1992, 91: 209–214

    Article  MathSciNet  MATH  Google Scholar 

  23. Fan H, Widera G E O. On the proper boundary conditions for a beam. J Appl Mech, 1992, 59: 915–922

    MathSciNet  MATH  Google Scholar 

  24. Timoshenko S P, Goodier J C. Theory of Elasticity. New York: McGraw-Hill, 1970

    MATH  Google Scholar 

  25. Zhao B S, Wang M Z. The equivalence of the refined theory and the decomposed theorem of an elastic plate. Appl Math Mech, 2005, 26: 486–494

    MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Science, China Agricultural University, Beijing, 100083, China

    Gao Yang

  2. State Key Laboratory for Turbulence and Complex Systems and Department of Mechanics and Engineering Science, Peking University, Beijing, 100871, China

    Wang Minzhong

Authors
  1. Gao Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Wang Minzhong
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Gao Yang.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Gao, Y., Wang, M. The refined theory of deep rectangular beams based on general solutions of elasticity. SCI CHINA SER G 49, 291–303 (2006). https://doi.org/10.1007/s11433-006-0291-0

Download citation

  • Received:

  • Accepted:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11433-006-0291-0

Keywords

Search

Navigation