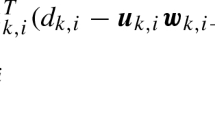Abstract
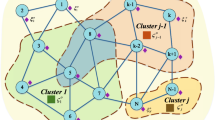
In this paper, we study the problem of distributed normalized least-mean squares (NLMS) estimation over multi-agent networks, where all nodes collaborate to estimate a common parameter of interest. We consider the situations that all nodes in the network are corrupted by both input and output noise. This yields into biased estimates by the distributed NLMS algorithms. In our analysis, we take all the noise into consideration and prove that the bias is dependent on the input noise variance. Therefore, we propose a bias compensation method to remove the noise-induced bias from the estimated results. In our development, we first assume that the variances of the input noise are known a priori and develop a series of distributed-based bias-compensated NLMS (BCNLMS) methods. Under various practical scenarios, the input noise variance is usually unknown a priori, therefore it is necessary to first estimate for its value before bias removal. Thus, we develop a real-time estimation method for the input noise variance, which overcomes the unknown property of this noise. Moreover, we perform some main analysis results of the proposed distributed BCNLMS algorithms. Furthermore, we illustrate the performance of the proposed distributed bias compensation method via graphical simulation results.
Similar content being viewed by others
References
Golub G H, van Loan C F. An analysis of the total least squares problem. SIAM J Numer Anal, 1980, 17: 883–893
Feng D Z, Zhang X D, Chang D X, et al. A fast recursive total least squares algorithm for adaptive FIR filtering. IEEE Trans Signal Process, 2004, 52: 2729–2737
So H C. Modified LMS algorithm for unbiased impulse response estimation in nonstationary noise. Electron Lett, 1999, 35: 791–792
Feng D Z, Bao Z, Zhang X D. Modified RLS algorithm for unbiased estimation of FIR system with input and output noise. Electron Lett, 2000, 36: 273–274
Sardellitti S, Barbarossa S. Distributed RLS estimation for cooperative sensing in small cell networks. In: Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICCASP), Vancouver, 2013. 5283–5287
Lorenzo P D, Isufi E, Banelli P, et al. Distributed recursive least squares strategies for adaptive reconstruction of graph signals. In: Proceedings of the 25th European Signal Processing Conference (EUSIPCO), Kos, 2017. 2289–2293
He X K, Xue W C, Fang H T. Consistent distributed state estimation with global observability over sensor network. 2017. ArXiv:1711.04993
He X K, Hu C, Xue W C, et al. On event-based distributed Kalman filter with information matrix triggers. IFAC-PapersOnLine, 2017, 50: 14308–14313
Lopes C G, Sayed A H. Incremental adaptive strategies over distributed networks. IEEE Trans Signal Process, 2007, 55: 4064–4077
Mostafapour E, Hoseini A, Nourinia J, et al. Channel estimation with adaptive incremental strategy over distributed sensor networks. In: Proceedings of the 2nd International Conference on Knowledge-Based Engineering and Innovation (KBEI), Tehran, 2015. 803–807
Lopes C G, Sayed A H. Distributed adaptive incremental strategies: formulation and performance analysis. In: Proceedings of IEEE International Conference on Acoustics Speech and Signal Processing Proceedings (ICASSP), Toulouse, 2006. 584–587
Shi L, Zhao H Q. Variable step-size distributed incremental normalised LMS algorithm. Electron Lett, 2016, 52: 519–521
Schizas I D, Mateos G, Giannakis G B. Distributed LMS for consensus-based in-network adaptive processing. IEEE Trans Signal Process, 2009, 57: 2365–2382
Braca P, Marano S, Matta V. Running consensus in wireless sensor networks. In: Proceedings of the 11th International Conference on Information Fusion (ICIF), Cologne, 2008
Kar S, Moura J M F. Distributed consensus algorithms in sensor networks with imperfect communication: link failures and channel noise. IEEE Trans Signal Process, 2009, 57: 355–369
Bogdanović N, Plata-Chaves J, Berberidis K. Distributed diffusion-based LMS for node-specific parameter estimation over adaptive networks. In: Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, 2014. 7223–7227
Nassif R, Richard C, Chen J, et al. Diffusion LMS over multitask networks with noisy links. In: Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, 2016. 4583–4587
Lee H S, Kim S E, Lee J W, et al. A variable step-size diffusion LMS algorithm for distributed estimation. IEEE Trans Signal Process, 2015, 63: 1808–1820
Cattivelli F S, Lopes C G, Sayed A H. Diffusion recursive least-squares for distributed estimation over adaptive networks. IEEE Trans Signal Process, 2008, 56: 1865–1877
Lopes C G, Sayed A H. Diffusion least-mean squares over adaptive networks: formulation and performance analysis. IEEE Trans Signal Process, 2008, 56: 3122–3136
Mateos G, Schizas I D, Giannakis G B. Distributed recursive least-squares for consensus-based in-network adaptive estimation. IEEE Trans Signal Process, 2009, 57: 4583–4588
Cattivelli F S, Sayed A H. Diffusion LMS strategies for distributed estimation. IEEE Trans Signal Process, 2010, 58: 1035–1048
Bertrand A, Moonen M, Sayed A H. Diffusion bias-compensated RLS estimation over adaptive networks. IEEE Trans Signal Process, 2011, 59: 5212–5224
Bertrand A, Moonen M. Consensus-based distributed total least squares estimation in Ad hoc wireless sensor networks. IEEE Trans Signal Process, 2011, 59: 2320–2330
Bertrand A, Moonen M, Sayed A H. Diffusion-based bias-compensated RLS for distributed estimation over adaptive sensor networks. In: Proceedings of the 19th European Signal Processing Conference (EUSIPCO), Barcelona, 2011. 1025–1029
Abdolee R, Champagne B, Sayed A H. A diffusion LMS strategy for parameter estimation in noisy regressor applications. In: Proceedings of the 20th European Signal Processing Conference (EUSIPCO), Bucharest, 2012. 749–753
Sayed A H. Adaptive Filters. Hoboken: Wiley, 2008
Haykin S. Adaptive Filter Theory. Englewood Cliffs: Prentice-Hall, 2002
Nagumo J, Noda A. A learning method for system identification. IEEE Trans Autom Control, 1967, 12: 282–287
Lou J, Jia L J, Tao R, et al. Distributed incremental bias-compensated RLS estimation over multi-agent networks. Sci China Inf Sci, 2017, 60: 032204
Acknowledgements
This work was supported by National Natural Science Foundation of China (Grant No. 61421001).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Fan, L., Jia, L., Tao, R. et al. Distributed bias-compensated normalized least-mean squares algorithms with noisy input. Sci. China Inf. Sci. 61, 112210 (2018). https://doi.org/10.1007/s11432-018-9461-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11432-018-9461-3