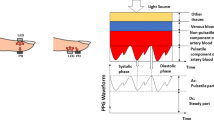
Abstract
One of the most important applications of photoplethysmography (PPG) signal is heartrate (HR) estimation. For its applications in wearable devices, motion artifact (MA) may be the most serious challenge for randomness both in format and temporal distribution. This paper proposes an advanced time-frequency analysis framework based on empirical mode decomposition (EMD) to select specific time slices for signal reconstruction. This framework operates with a type of pre-processing called variance characterization series (VCS), EMD, singular value decomposition (SVD), and a precise and adaptive 2-D filtration reported first. This filtration is based on Harr wavelet transform (HWT) and 3rd order cumulant analysis, to make it have resolution in both the time domain and different components. The simulation results show that the proposed method gains 1.07 in absolute average error (AAE) and 1.87 in standard deviation (SD); AAEs’ 1st and 3rd quartiles are 0.12 and 1.41, respectively. This framework is tested by the PhysioBank MIMIC II waveform database.
Similar content being viewed by others
References
Selvaraj N, Jaryal A, Santhosh J, et al. Assessment of heart rate variability derived from finger-tip photoplethysmography as compared to electrocardiography. J Med Eng Technol, 2008, 32: 479–484
Petersen C L, Chen T P, Ansermino J M, et al. Design and evaluation of a low-cost smartphone pulse oximeter. Sensors, 2013, 13: 16882–16893
Lee J, Jung W. Design the filter to reject motion artifact of pulse oximetry. Elsevier Comput Sci, 2003, 26: 241–249
Zhang Z, Pi Z, Liu B. TROIKA: a general framework for heart rate monitoring using wrist-type photoplethysmographic signals during intensive physical exercise. IEEE Trans Biomed Eng, 2015, 62: 522–531
Murthy N K L, Madhusudana P C, Suresha P, et al. Multiple spectral peak tracking for heart rate monitoring from photoplethysmography signal during intensive physical exercise. IEEE Signal Process Lett, 2015, 22: 2391–2395
Komaty A, Boudraa A O, Augier B, et al. EMD-based filtering using similarity measure between probability density functions of IMFs. IEEE Trans Instrum Meas, 2014, 63: 27–34
Yang G, Liu Y, Wang Y, et al. EMD interval thresholding denoising based on similarity measure to select relevant modes. Signal Process, 2015, 109: 95–109
Sung P, Syed Z, Guttag J. Quantifying morphology changes in time series data with skew. In: Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing, ICASSP 2009, Taipei, 2009. 477–480
Wu Z, Huang N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method. Adv Adapt Data Anal, 2009, 1: 1–41
Motin M A, Karmakar C, Palaniswami M. Ensemble empirical mode decomposition with principal component analysis: a novel approach for extracting respiratory rate and heart rate from photoplethysmographic signal. IEEE J Biomed Health Inf, 2017. doi: 10.1109/JBHI.2017.2679108
Pang B, Liu M, Zhang X, et al. Advanced EMD method using variance characterization for PPG with motion artifact. In: Proceedings of 2016 IEEE Biomedical Circuits and Systems Conference (BioCAS), Shanghai, 2016. 196–199
Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc Math Phys Eng Sci, 1998, 454: 903–995
Li P, Liu M, Zhang X, et al. A low-complexity ECG processing algorithm based on the Haar wavelet transform for portable health-care devices. Sci China Inf Sci, 2014, 57: 122303
Gao Y, Ge G, Sheng Z, et al. Analysis and solution to the mode mixing phenomenon in EMD. Congress Image Signal Process, 2008, 5: 223–227
Dimitrakopoulos R, Mustapha H, Gloaguen E. High-order statistics of spatial random fields: exploring spatial cumulants for modeling complex non-Gaussian and non-linear phenomena. Math Geosci, 2010, 42: 65–99
Donoho D L. De-noising by soft-thresholding. IEEE Trans Inf Theory, 1995, 41: 613–627
Li X, Zhang X, Li P, et al. An 8.12 W wavelet denoising chip for PPG detection and portable heart rate monitoring in 0.18 µm CMOS. J Semicond, 2016, 37: 055006
Zhang Z. Photoplethysmography-based heart rate monitoring in physical activities via joint sparse spectrum reconstruction. IEEE Trans Biomed Eng, 2015, 62: 1902–1910
Acknowledgments
This work was supported by National Natural Science Foundation of China (Grant Nos. 61634006, 61372060, 61335010, 61474107, 81300803), National Key Technologies R&D Program (Grant Nos. 2016YFB0401303, 2016YFB0402405), Basic Research Project of Shanghai Science and Technology Commission (Grant No. 16JC1400101), and Key Research Program of Frontier Science, Chinese Academy of Sciences (Grant No. QYZDY-SSW-JSC004).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Pang, B., Liu, M., Zhang, X. et al. A novel approach framework based on statistics for reconstruction and heartrate estimation from PPG with heavy motion artifacts. Sci. China Inf. Sci. 61, 022312 (2018). https://doi.org/10.1007/s11432-017-9168-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11432-017-9168-2