Abstract
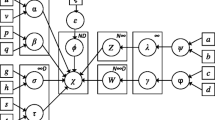
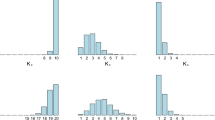
This study presents a novel approach to unsupervised learning for clustering with missing data. We first extend a finite mixture model to the infinite case by considering Dirichlet process mixtures, which can automatically determine the number of mixture components or clusters. Furthermore, we view the missing features as latent variables and compute the posterior distributions using the variational Bayesian expectation maximization algorithm, which optimizes the evidence lower bound on the complete-data log marginal likelihood. We demonstrate the performance on several artificial data sets with missing values. The experimental results indicate that the proposed method outperforms some classic imputation methods. We finally present an application to seabed hydrothermal sulfide color images analysis problem.
创新点
本文提出了一种能够用于处理缺失数据的无监督聚类学习方法。首先,我们将Dirichlet过程作为先验分布引入到有限混合模型中,实现聚类数目或混合成分数的自动识别。其次,针对观测样本不同维度数据存在缺失的问题,我们将缺失成分当成隐变量参数,利用变分贝叶斯期望最大化算法优化完全观测数据边际似然函数的下界,对参数的后验分布进行求解。通过和几种典型的插补方法进行对比实验,验证了本文所提出方法的有效性。最后,将该方法应用于深海热液硫化物图像分析,完成图像的自动分类任务。
Similar content being viewed by others
References
Li C Z, Xu Z B, Qiao C, et al. Hierarchical clustering driven by cognitive features. Sci China Inf Sci, 2014, 57: 012109
Wu C M, Chou S C, Liaw H T. A trend based investment decision approach using clustering and heuristic algorithm. Sci China Inf Sci, 2014, 57: 092117
McLachlan G, Peel D. Finite Mixture Models. Hoboken: John Wiley and Sons, 2004
Fan W, Bouguila N. Variational learning of a Dirichlet process of generalized Dirichlet distributions for simultaneous clustering and feature selection. Pattern Recogn, 2013, 46: 2754–2769
Figueiredo M A T, Jain A K. Unsupervised learning of finite mixture models. IEEE Trans Pattern Anal Mach Intell, 2002, 24: 381–396
Neal R M. Markov chain sampling methods for Dirichlet process mixture models. J Comput Graph Stat, 2000, 9: 249–265
Blei D M, Jordan M I. Variational inference for Dirichlet process mixtures. Bayesian Anal, 2006, 1: 121–143
Kim S, Tadesse M G, Vannucci M. Variable selection in clustering via Dirichlet process mixture models. Biometrika, 2006, 93: 877–893
Orbanz P, Buhmann J M. Nonparametric Bayesian image segmentation. Int J Comput Vision, 2008, 77: 25–45
García-Laencina P J, Sancho-Gómez J L, Figueiras-Vidal A R. Pattern classification with missing data: a review. Neural Comput Appl, 2010, 19: 263–282
Wang C, Liao X, Carin L, et al. Classification with incomplete data using Dirichlet process priors. J Mach Learn Res, 2010, 11: 3269–3311
Williams D, Liao X J, Xue Y, et al. On classification with incomplete data. IEEE Trans Pattern Anal Mach Intell, 2007, 29: 427–436
Schafer J L, Graham J W. Missing data: our view of the state of the art. Psychol Method, 2002, 7: 147–177
Little R J A, Rubin D B. Statistical Analysis with Missing Data. 2nd ed. Hoboken: John Wiley and Sons, 2002
Chechik G, Heitz G, Elidan G, et al. Max-margin classification of data with absent features. J Mach Learn Res, 2008, 9: 1–21
Fidler S, Skocaj D, Leonardis A. Combining reconstructive and discriminative subspace methods for robust classification and regression by subsampling. IEEE Trans Pattern Anal Mach Intell, 2006, 28: 337–350
Chan K, Lee T W, Sejnowski T J. Variational learning of clusters of undercomplete nonsymmetric independent components. J Mach Learn Res, 2003, 3: 99–114
Teh Y W, Jordan M I, Beal M J, et al. Hierarchical dirichlet processes. J Amer Stat Assoc, 2006, 101: 1566–1581
Sethuraman J. A constructive definition of Dirichlet priors. Stat Sin, 1994, 4: 639–650
Ghahramani Z, Beal M J. Propagation algorithms for variational Bayesian learning. In: Leen T K, Dietterich T, Tresp V, eds. Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2001. 507–513
Hughes M C, Sudderth E. Memoized online variational inference for Dirichlet process mixture models. In: Burges C J C, Bottou L, Welling M, et al, eds. Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2013. 1133–1141
Bishop C M. Pattern Recognition and Machine Learning. New York: springer, 2006
Lin T I, Lee J C, Ho H J. On fast supervised learning for normal mixture models with missing information. Pattern Recogn, 2006, 39: 1177–1187
Collins L M, Schafer J L, Kam C M. A comparison of inclusive and restrictive strategies in modern missing data procedures. Psychol Method, 2001, 6: 330–351
Meng X L, Rubin D B. Maximum likelihood estimation via the ECM algorithm: a general framework. Biometrika, 1993, 80: 267–278
Ueda N, Nakano R. Deterministic annealing EM algorithm. Neural Netw, 1998, 11: 271–282
Barnard K, Duygulu P, Forsyth D, et al. Matching words and pictures. J Mach Learn Res, 2003, 3: 1107–1135
Herzig P M, Hannington M D. Polymetallic massive sulfides at the modern seafloor a review. Ore Geol Rev, 1995, 10: 95–115
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Zhang, X., Song, S., Zhu, L. et al. Unsupervised learning of Dirichlet process mixture models with missing data. Sci. China Inf. Sci. 59, 1–14 (2016). https://doi.org/10.1007/s11432-015-5429-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11432-015-5429-0