Abstract
In this paper, we propose a range reconstruction method for a frequency-band shared multipleinput multiple-output (MIMO) orthogonal frequency-division multiplexing (OFDM) radar with sufficient cyclic prefix (CP) by using real orthogonal designs. Compared with the application of complex orthogonal designs in our previous work, the application of real orthogonal designs can significantly reduce the number of the all-zero-valued pulses in a coherent processing interval (CPI) for each transmitter and increase the efficiency of radar transmitters. Meanwhile, it still maintains the advantages of full spatial diversity without inter-range-cell interference (IRCI). We also apply the rate-1 real orthogonal designs for different numbers of transmitters and pulses for range reconstruction without any idleness of radar transmitters. Simulation results are presented to illustrate the performances of the OFDM pulse design and the CP-based MIMO OFDM radar using real orthogonal designs.
摘要
创新点
-
1.
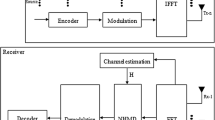
在共享频谱的情况下, 提出了基于循环前缀的MIMO OFDM 雷达回波模型。
-
2.
提出了 MIMO OFDM 雷达联合脉冲压缩和脉冲相干积累算法, 当循环前缀长度充足时, 在不同发射信号共享频谱的情况下, 实现不同发射信号频域子带的正交性, 并实现无距离旁瓣脉冲压缩。
-
3.
结合实正交设计, 提出了基于 Paraunitary 滤波器组和迭代 Clipping 加滤波的两种 MIMO OFDM 波形设计算法, 实现了任意长度 MIMO OFDM 发射脉冲的联合脉冲压缩和脉冲相干积累, 并保持了不同发射信号的无互扰和无距离旁瓣脉冲压缩。
Similar content being viewed by others
References
Li J, Stoica P. MIMO radar with colocated antennas. IEEE Signal Process Mag, 2007, 24: 106–114
Li J, Stoica P. MIMO Radar Signal Processing. New York: Wiley Online Library, 2008
Wu X H, Kishk A A, Glisson A W. MIMO-OFDM radar for direction estimation. IET Radar Sonar Nav, 2010, 4: 28–36
Cao Y-H, Xia X-G, Wang S-H. IRCI free co-located MIMO radar based on sufficient cyclic prefix OFDM waveforms. IEEE Trans Aerosp Electron Syst, 2015, 51: 2107–2120
Cao Y-H, Xia X-G. IRCI-free MIMO-OFDM SAR using circularly shifted Zadoff-Chu sequences. IEEE Geosci Remote Sens Lett, 2015, 12: 1126–1130
Meng C Z, Xu J, Xia X-G, et al. MIMO-SAR waveforms separation based on virtual polarization filter. Sci China Inf Sci, 2015, 58: 042301
He F, Chen Q, Dong Z, et al. Modeling and high-precision processing of the azimuth shift variation for spaceborne HRWS SAR. Sci China Inf Sci, 2013, 56: 102304
Haimovich A M, Blum R S, Cimini L J. MIMO radar with widely separated antennas. IEEE Signal Process Mag, 2008, 25: 116–129
Chernyak V. Multisite radar systems composed of MIMO radars. IEEE Aerospace Electron Syst Mag, 2014, 29: 28–37
Xu J, Dai X-Z, Xia X-G, et al. Optimizations of multisite radar system with MIMO radars for target detection. IEEE Trans Aerospace Electron Syst, 2011, 47: 2329–2343
Antonio G S, Fuhrmann D R, Robey F C. MIMO radar ambiguity functions. IEEE J Sel Topics Signal Process, 2007, 1: 167–177
Somaini U. Binary sequences with good autocorrelation and cross correlation properties. IEEE Trans Aerospace Electron Syst, 1975, 11: 1226–1231
Deng H. Synthesis of binary sequences with good autocorrelation and crosscorrelation properties by simulated annealing. IEEE Trans Aerospace Electron Syst, 1996, 32: 98–107
Deng H. Polyphase code design for orthogonal netted radar systems. IEEE Trans Signal Process, 2004, 52: 3126–3135
Khan H A, Zhang Y Y, Ji C L, et al. Optimizing polyphase sequences for orthogonal netted radar. IEEE Signal Process Lett, 2006, 13: 589–592
He H, Stoica P, Li J. Designing unimodular sequence sets with good correlations-Including an application to MIMO radar. IEEE Trans Signal Process, 2009, 57: 4391–4405
Song X F, Zhou S L, Willett P. Reducing the waveform cross correlation of MIMO radar with space-time coding. IEEE Trans Signal Process, 2010, 58: 4213–4224
Xu L, Liang Q L. Zero correlation zone sequence pair sets for MIMO radar. IEEE Trans Aerospace Electron Syst, 2012, 48: 2100–2113
Jin Y, Wang H, Jiang W, et al. Complementary-based chaotic phase-coded waveforms design for MIMO radar. IET Radar Sonar Nav, 2013, 7: 371–382
Xia X-G, Zhang T X, Kong L J. MIMO OFDM radar IRCI free range reconstruction with sufficient cyclic prefix. IEEE Trans Aerospace Electron Syst, 2015, 51: 2276–2293
Zhang T X, Xia X-G. OFDM synthetic aperture radar imaging with sufficient cyclic prefix. IEEE Trans Geosci Remote Sens, 2015, 53: 394–404
Zhang T X, Xia X-G, Kong L J. IRCI free range reconstruction for SAR imaging with arbitrary length OFDM pulse. IEEE Trans Signal Process, 2014, 62: 4748–4759
Kim J-H, Younis M, Moreira A, et al. A novel OFDM chirp waveform scheme for use of multiple transmitters in SAR. IEEE Geosci Remote Sens Lett, 2013, 10: 568–572
Sit Y L, Sturm C, Baier J, et al. Direction of arrival estimation using the MUSIC algorithm for a MIMO OFDM radar. In: Proceedings of IEEE Radar Conference, Atlanta, 2012. 0226–0229
Sen S, Nehorai A. OFDM MIMO radar with mutual-information waveform design for low-grazing angle tracking. IEEE Trans Signal Process, 2010, 58: 3152–3162
Lu K J, Fu S L, Xia X-G. Closed-form designs of complex orthogonal space-time block codes of rates (k + 1)/(2k) for 2k - 1 or 2k transmit antennas. IEEE Trans Inf Theory, 2005, 51: 4340–4347
Liang X-B. Orthogonal designs with maximal rates. IEEE Trans Inf Theory, 2003, 49: 2468–2503
Geramita A V, Seberry J. Orthogonal Designs, Quadratic Forms and Hadamard Matrices, Lecture Notes in Pure and Applied Mathematics, Vol. 43. New York and Basel: Marcel Dekker, 1979
Armstrong J. Peak-to-average power reduction for OFDMby repeated clipping and frequency domain filtering. Electron Lett, 2002, 38: 246–247
Han S H, Lee J H. An overview of peak-to-average power ratio reduction techniques for multicarrier transmission. IEEE Wirel Commun, 2005, 12: 56–65
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Zhang, T., Xia, XG. & Kong, L. CP-based MIMO OFDM radar IRCI free range reconstruction using real orthogonal designs. Sci. China Inf. Sci. 60, 022301 (2017). https://doi.org/10.1007/s11432-015-0979-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11432-015-0979-5
Keywords
- cyclic prefix (CP)
- inter-range-cell interference (IRCI)
- multiple-input multiple-output (MIMO) radar
- real orthogonal designs
- orthogonal frequency division multiplexing (OFDM) pulse