Skip to main content
SpringerLink
Log in

Neural FIR adaptive Laguerre equalizer with a gradient adaptive amplitude for nonlinear channel in communication systems

  • Published:
Science in China Series F: Information Sciences Aims and scope Submit manuscript

Abstract

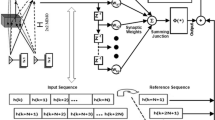
To mitigate the linear and nonlinear distortions in communication systems, two novel nonlinear adaptive equalizers are proposed on the basis of the neural finite impulse response (FIR) filter, decision feedback architecture and the characteristic of the Laguerre filter. They are neural FIR adaptive decision feedback equalizer (SNNDFE) and neural FIR adaptive Laguerre equalizer (LSNN). Of these two equalizers, the latter is simple and with characteristics of both infinite impulse response (IIR) and FIR filters; it can use shorter memory length to obtain better performance. As confirmed by theoretical analysis, the novel LSNN equalizer is stable (0 <a<1). Furthermore, simulation results show that the SNNDFE can get better equalized performance than SNN equalizer, while the latter exhibits better performance than others in terms of convergence speed, mean square error (MSE) and bit error rate (BER). Therefore, it can reduce the input dimension and eliminate linear and nonlinear interference effectively. In addition, it is very suitable for hardware implementation due to its simple structure.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Proakis J G. Digital Communications. 4th ed. New York: McGraw-Hill, 2000

    Google Scholar 

  2. Haykin S. Adaptive Filter Theory. 4th ed. Englewood Cliffs, NJ: Prentice-Hall, 2001

    Google Scholar 

  3. Qureshi S. Adaptive equalization. Proc IEEE, 1985, 73(9): 1349–1387

    Article  Google Scholar 

  4. Gibson G J, Sin S, Cowan C F N. Application of multilayer perceptions as adaptive equalizer. In: Proc of IEEE Int Conf on ASSP, Glasgow, Scotland, 1989. 1183–1186

  5. Gibson G J, Sin S, Cowan C F N. The application of nonlinear structures to the reconstruction of binary signals. IEEE Trans Signal Process, 1991, 39(8): 1877–1885

    Article  Google Scholar 

  6. Chen S, Gibson G. J, Cowan C F N, et al. Reconstruction of binary of signals using an adaptive radial-basis-function equalizer. Signal Process, 1991, 22(1): 77–93

    Article  Google Scholar 

  7. Cha I, Kassam S A. Channel equalization using adaptive complex radial basis function networks. IEEE J Select Area Commun, 1995, 13(1): 122–131

    Article  Google Scholar 

  8. Chen S, Mulgrew B, Grant P M. A clustering technique for digital communication channel equalization using radial basis function networks. IEEE Trans Neural Netw, 1993, 4(4): 570–579

    Article  Google Scholar 

  9. Chen S, Mulgrrew B. Overcoming co-channel interference using an adaptive radial basis function equalizer. Signal Process, 1992, 28: 91–107

    Article  Google Scholar 

  10. Kechriotis G, Zervas E, Manolakos E S. Using recurrent neural networks for adaptive communication channel equalization. IEEE Trans Neural Netw, 1994, 5(2): 267–278

    Article  Google Scholar 

  11. Mandic D P. NNGD algorithm for neural adaptive filters. Electron Lett, 2000, 39(9): 845–846

    Article  Google Scholar 

  12. Mandic D P, Hanna A I, Razaz M. A normalized gradient descent algorithm for nonlinear adaptive filters using gradient adaptive step size. IEEE Signal Process Lett, 2001, 8(11): 295–297

    Article  Google Scholar 

  13. Hanna A I, Mandic D P. Nonlinear FIR adaptive filters with a gradient adaptive amplitude in the nonlinearity. IEEE Signal Process Lett, 2002, 9(8): 253–255

    Article  Google Scholar 

  14. Mandic D P, Krcmar I R. Stability of NNGD algorithm for nonlinear system identification. Electron Lett, 2001, 37(3): 200–202

    Article  Google Scholar 

  15. Wahlberg B. System identification using Laguerre models. IEEE Trans Autom Control, 1991, 36: 551–562

    Article  MATH  MathSciNet  Google Scholar 

  16. Makila P M. Approximation of stable systems by Laguerre filters. Automatica, 1990, 26: 333–345

    Article  MathSciNet  Google Scholar 

  17. Silva O T. On the determination of the optimal pole position of Laguerre filters. IEEE Trans Signal Process, 1995, 43(9): 2079–2087

    Article  Google Scholar 

  18. Wang L, Cluett W R. Optimal choice of time-scaling factors for linear system approximations using Laguerre models. IEEE Trans Autom Control, 1994, 39(7): 1463–1467

    Article  MATH  MathSciNet  Google Scholar 

  19. Hung F Y, Zhang J S. A novel nonlinear adaptive prediction filter for narrowband interference suppression in DS-SS communication. J Electron Inf Tech, 2007, 29(6): 1328–1331

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Key Laboratory of Signal and Information Processing of Sichuan Province, Southwest Jiaotong University, Chengdu, 610031, China

    HaiQuan Zhao & JiaShu Zhang

Authors
  1. HaiQuan Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. JiaShu Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to HaiQuan Zhao.

Additional information

Supported partially by the National Natural Science Foundation of China (Grant No. 60971104), the Program for New Century Excellent Talents in University of China (Grant No. NCET-05-0794), and the Doctoral Innovation Fund of Southwest Jiaotong University

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zhao, H., Zhang, J. Neural FIR adaptive Laguerre equalizer with a gradient adaptive amplitude for nonlinear channel in communication systems. Sci. China Ser. F-Inf. Sci. 52, 1881–1890 (2009). https://doi.org/10.1007/s11432-009-0148-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11432-009-0148-z

Keywords

Search

Navigation