Skip to main content
SpringerLink
Log in

A novel obstacle avoidance heuristic algorithm of continuum robot based on FABRIK

  • Article
  • Published:
Science China Technological Sciences Aims and scope Submit manuscript

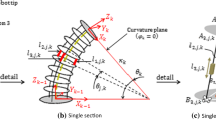
Abstract

Obstacle avoidance and path planning of continuum robots are challenging tasks due to the hyper-redundant degree of freedoms (DOFs) and restricted working environments. Meanwhile, most current heuristic algorithm-based obstacle avoidance algorithms exist with low computational efficiency, complex solution process, and inability to add global constraints. This paper proposes a novel obstacle avoidance heuristic algorithm based on the forward and backward reaching inverse kinematics (FABRIK) algorithm The update of key nodes in this algorithm is modeled as the movement of charges in an electric field, avoiding complex nonlinear operations The algorithm achieves the robustness of inverse kinematics and path tracking in complex environments by imposing constraints on key nodes and determining the location of obstacles in advance This algorithm is characterized by a high convergence rate, low computational cost, and can be used for real-time applications. The proposed approach also has wide applicability and can be applied to both mobile and fixed-base continuum robots And it can be further extended to the field of hyper-redundant robots. The algorithm’s effectiveness is further validated by simulating the path tracking and obstacle avoidance of a five-segment continuum robot in various environments and comparisons with classical methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Webster Iii R J, Jones B A. Design and kinematic modeling of constant curvature continuum robots: A review. Int J Robot Res, 2010, 29: 1661–1683

    Article  Google Scholar 

  2. Xu K, Zhao J, Fu M. Development of the SJTU unfoldable robotic system (SURS) for single port laparoscopy. IEEE ASME Trans Mechatron, 2014, 20: 2133–2145

    Article  Google Scholar 

  3. Burgner-Kahrs J, Rucker D C, Choset H. Continuum robots for medical applications: A survey. IEEE Trans Robot, 2015, 31: 1261–1280

    Article  Google Scholar 

  4. Buckingham R, Chitrakaran V, Conkie R, et al. Snake-arm robots: A new approach to aircraft assembly. SAE Technical Paper. Los Angeles, 2007

  5. Gong Z, Fang X, Chen X, et al. A soft manipulator for efficient delicate grasping in shallow water: Modeling, control, and real-world experiments. Int J Robot Res, 2021, 40: 449–469

    Article  Google Scholar 

  6. Buckingham R O, Graham A C. Dexterous manipulators for nuclear inspection and maintenance—Case study. In: 2010 1st International Conference on Applied Robotics for the Power Industry. Montreal, 2010. 1–6

  7. Tang L, Huang J, Zhu L M, et al. Path tracking of a cable-driven snake robot with a two-level motion planning method. IEEE ASME Trans Mechatron, 2019, 24: 935–946

    Article  Google Scholar 

  8. Li S, Hao G. Current trends and prospects in compliant continuum robots: A survey. Actuators, 2021, 10: 145

    Article  Google Scholar 

  9. Dulęba I, Opałka M. A comparison of Jacobian-based methods of inverse kinematics for serial robot manipulators. Int J Appl Math Comput Sci, 2013, 23: 373–382

    Article  MathSciNet  MATH  Google Scholar 

  10. Lee K K, Buss M. Obstacle avoidance for redundant robots using Jacobian transpose method. In: 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems. San Diego, 2007. 3509–3514

  11. Aristidou A, Lasenby J, Chrysanthou Y, et al. Inverse kinematics techniques in computer graphics: A survey. Comput Graphics Forum, 2018, 37: 35–58

    Article  Google Scholar 

  12. Thuruthel T G, Shih B, Laschi C, et al. Soft robot perception using embedded soft sensors and recurrent neural networks. Sci Robot, 2019, 4: eaav1488

    Article  Google Scholar 

  13. Tutsoy O, Erol Barkana D, Colak S. Learning to balance an NAO robot using reinforcement learning with symbolic inverse kinematic. Trans Inst Meas Control, 2017, 39: 1735–1748

    Article  Google Scholar 

  14. Wu J, Zhang B B, Wang L P, et al. An iterative learning method for realizing accurate dynamic feedforward control of an industrial hybrid robot. Sci China Tech Sci, 2021, 64: 1177–1188

    Article  Google Scholar 

  15. George Thuruthel T, Ansari Y, Falotico E, et al. Control strategies for soft robotic manipulators: A survey. Soft Robot, 2018, 5: 149–163

    Article  Google Scholar 

  16. Gao Y, Takagi K, Kato T, et al. Continuum robot with follow-the-leader motion for endoscopic third ventriculostomy and tumor biopsy. IEEE Trans Biomed Eng, 2019, 67: 379–390

    Article  Google Scholar 

  17. Cho C N, Jung H, Son J, et al. An intuitive control algorithm for a snake-like natural orifice transluminal endoscopic surgery platform: A preliminary simulation study. Biomed Eng Lett, 2016, 6: 39–46

    Article  Google Scholar 

  18. Palmer D, Cobos-Guzman S, Axinte D. Real-time method for tip following navigation of continuum snake arm robots. Robot Auton Syst, 2014, 62: 1478–1485

    Article  Google Scholar 

  19. Kenwright B. Inverse kinematics—Cyclic coordinate descent (CCD). J Graphics Tools, 2012, 16: 177–217

    Article  Google Scholar 

  20. Mahmudi M, Kallmann M. Feature-based locomotion with inverse branch kinematics. In: International Conference on Motion in Games. Heidelberg, 2011. 39–50

  21. Muller-Cajar R, Mukundan R. Triangualation: A new algorithm for inverse kinematics. In: Proceedings of Image and Vision Computing New Zealand 2007. Hamilton, 2007. 181–186

  22. Aristidou A, Lasenby J. FABRIK: A fast, iterative solver for the inverse kinematics problem. Graphical Model, 2011, 73: 243–260

    Article  Google Scholar 

  23. Ananthanarayanan H, Ordóñez R. Real-time inverse kinematics of (2n +1) DOF hyper-redundant manipulator arm via a combined numerical and analytical approach. Mech Mach Theory, 2015, 91: 209–226

    Article  Google Scholar 

  24. Liu T, Yang T, Xu W, et al. Efficient inverse kinematics and planning of a hybrid active and passive cable-driven segmented manipulator. IEEE Trans Syst Man Cybern Syst, 2022, 52: 4233–4246

    Article  Google Scholar 

  25. Dong G, Huang P, Wang Y, et al. A modified forward and backward reaching inverse kinematics based incremental control for space manipulators. Chin J Aeronaut, 2021, doi: https://doi.org/10.1016/j.cja.2021.08.014

  26. Kavraki L E, Svestka P, Latombe J C, et al. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans Robot Automat, 1996, 12: 566–580

    Article  Google Scholar 

  27. Kuffner J J, LaValle S M. RRT-connect: An efficient approach to single-query path planning. In: Proceedings 2000 ICRA. Millennium Conference. IEEE International Conference on Robotics and Automation. San Francisco, 2000. 995–1001

  28. Niu G, Wang L, Gao Q, et al. Path-tracking algorithm for aircraft fuel tank inspection robots. Int J Adv Robot Syst, 2014, 11: 82

    Article  Google Scholar 

  29. Niu G, Zhang Y, Li W. Path planning of continuum robot based on path fitting. J Control Sci Eng, 2020, 2020: 8826749

    Article  MATH  Google Scholar 

  30. Tao S, Yang Y. Collision-free motion planning of a virtual arm based on the FABRIK algorithm. Robotica, 2017, 35: 1431–1450

    Article  Google Scholar 

  31. Coelho F O, Pinto M F, Souza J P C, et al. Hybrid methodology for path planning and computational vision applied to autonomous mission: A new approach. Robotica, 2020, 38: 1000–1018

    Article  Google Scholar 

  32. Huang Y, Ding H, Zhang Y, et al. A motion planning and tracking framework for autonomous vehicles based on artificial potential field elaborated resistance network approach. IEEE Trans Ind Electron, 2019, 67: 1376–1386

    Article  Google Scholar 

  33. Tian Y, Zhu X, Meng D, et al. An overall configuration planning method of continuum hyper-redundant manipulators based on improved artificial potential field method. IEEE Robot Autom Lett, 2021, 6: 4867–4874

    Article  Google Scholar 

  34. Gerget O M, Kolpashchikov D Y. Collision avoidance for continuum robot using FABRIK algorithm. In: 2019 Twelfth International Conference “Management of large-scale system development” (MLSD). Moscow, 2019. 1–4

  35. Santos P C, Freire R C S, Carvalho E A N, et al. M-FABRIK: A new inverse kinematics approach to mobile manipulator robots based on FABRIK. IEEE Access, 2020, 8: 208836–208849

    Article  Google Scholar 

  36. Ju R, Zhang D, Xu J, et al. Design, modeling, and kinematics analysis of a modular cable-driven manipulator. J Mech Robot, 2022, 14: 060903

    Article  Google Scholar 

  37. Wu J, Wang X, Zhang B, et al. Multi-objective optimal design of a novel 6-DOF spray-painting robot. Robotica, 2021, 39: 2268–2282

    Article  Google Scholar 

  38. Deng J, Meng B H, Kanj I, et al. Near-optimal smooth path planning for multisection continuum arms. In: Proceedings of 2nd IEEE International Conference on Soft Robotics (RoboSoft). Seoul: IEEE, 2009. 416–421

  39. Santoso J, Onal C D. An origami continuum robot capable of precise motion through torsionally stiff body and smooth inverse kinematics. Soft Robot, 2021, 8: 371–386

    Article  Google Scholar 

  40. Mohammad A, Russo M, Fang Y, et al. An efficient follow-the-leader strategy for continuum robot navigation and coiling. IEEE Robot Autom Lett, 2021, 6: 7493–7500

    Article  Google Scholar 

  41. Jones B A, Walker I D. Kinematics for multisection continuum robots. IEEE Trans Robot, 2006, 22: 43–55

    Article  Google Scholar 

  42. Jones B A, Walker I D. Practical kinematics for real-time implementation of continuum robots. IEEE Trans Robot, 2006, 22: 1087–1099

    Article  Google Scholar 

  43. Mahl T, Hildebrandt A, Sawodny O. A variable curvature continuum kinematics for kinematic control of the bionic handling assistant. IEEE Trans Robot, 2014, 30: 935–949

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Robotics Institute, Beihang University, Beijing, 100191, China

    HaoRan Wu, JingJun Yu & Jie Pan

  2. Department of Mechanical Design, Beihang University, Beijing, 100191, China

    Xu Pei

Authors
  1. HaoRan Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. JingJun Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jie Pan
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Xu Pei
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xu Pei.

Additional information

This work was supported by the National Natural Science Foundation of China (Grant No. U1813221) and the National Key Research and Development Program of China (Grant No. 2019YFB1311200).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wu, H., Yu, J., Pan, J. et al. A novel obstacle avoidance heuristic algorithm of continuum robot based on FABRIK. Sci. China Technol. Sci. 65, 2952–2966 (2022). https://doi.org/10.1007/s11431-022-2179-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11431-022-2179-9

Search

Navigation