Skip to main content
SpringerLink
Log in

Adaptive neural control of nonlinear periodic time-varying parameterized mixed-order multi-agent systems with unknown control coefficients

  • Article
  • Published:
Science China Technological Sciences Aims and scope Submit manuscript

Abstract

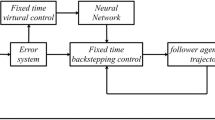
In this paper, we first consider the adaptive leader-following consensus problem for a class of nonlinear parameterized mixed-order multi-agent systems with unknown control coefficients and time-varying disturbance parameters of the same period. Neural networks and Fourier series expansions are used to describe the unknown nonlinear periodic time-varying parameterized function. A distributed control protocol is designed based on adaptive control, matrix theory, and Nussbaum function. The robustness of the distributed control protocol is analyzed by combining the stability analysis theory of closed-loop systems. On this basis, this paper discusses the case of time-varying disturbance parameters with non-identical periods, expanding the application scope of this control protocol. Finally, the effectiveness of the algorithm is verified by a simulation example.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Burgon R, Roberts P C E, Roberts J A, et al. Maneuver planning optimization for spacecraft formation flying missions. J Astronaut Sci, 2008, 56: 545–571

    Article  Google Scholar 

  2. Whitbrook A M, Aickelin U, Garibaldi J M. Idiotypic immune networks in mobile-robot control. IEEE Trans Syst Man Cybern B, 2007, 37: 1581–1598

    Article  Google Scholar 

  3. Sundar K, Rathinam S. Algorithms for routing an unmanned aerial vehicle in the presence of refueling depots. IEEE Trans Automat Sci Eng, 2014, 11: 287–294

    Article  Google Scholar 

  4. Li Z, Ren W, Liu X, et al. Distributed containment control of multi-agent systems with general linear dynamics in the presence of multiple leaders. Int J Robust Nonlin Control, 2013, 23: 534–547

    Article  MathSciNet  MATH  Google Scholar 

  5. Ren W, Beard R W, Atkins E M. Information consensus in multivehicle cooperative control. IEEE Control Syst Mag, 2007, 27: 71–82

    Article  Google Scholar 

  6. Liu W, Zhou S, Qi Y, et al. Leaderless consensus of multi-agent systems with Lipschitz nonlinear dynamics and switching topologies. Neurocomputing, 2016, 173: 1322–1329

    Article  Google Scholar 

  7. Gao R, Huang J, Wang L. Leaderless consensus control of uncertain multi-agents systems with sensor and actuator attacks. Inf Sci, 2019, 505: 144–156

    Article  MathSciNet  MATH  Google Scholar 

  8. Cui Q, Huang J, Gao T. Adaptive leaderless consensus control of uncertain multiagent systems with unknown control directions. Int J Robust Nonlin Control, 2020, 30: 6229–6240

    Article  MathSciNet  Google Scholar 

  9. Ao W, Huang J, Xue F. Adaptive leaderless consensus control of a class of strict-feedback nonlinear multi-agent systems with unknown control directions: a non-Nussbaum function based approach. J Franklin Inst, 2020, 357: 12180–12196

    Article  MathSciNet  MATH  Google Scholar 

  10. Zhang H, Lewis F L. Adaptive cooperative tracking control of higher-order nonlinear systems with unknown dynamics. Automatica, 2012, 48: 1432–1439

    Article  MathSciNet  MATH  Google Scholar 

  11. Chen J, Li J, Yuan X. Global fuzzy adaptive consensus control of unknown nonlinear multiagent systems. TREE Trans Fuzzy Syst, 2020, 28: 510–522

    Article  Google Scholar 

  12. He X Y, Wang Q Y, Hao Y Q. Finite-time adaptive formation control for multi-agent systems with uncertainties under collision avoidance and connectivity maintenance. Sci China Tech Sci, 2020, 63: 2305–2314

    Article  Google Scholar 

  13. Wang X X, Liu Z X, Chen Z Q. Event-triggered fault-tolerant consensus control with control allocation in leader-following multi-agent systems. Sci China Tech Sci, 2021, 64: 879–889

    Article  Google Scholar 

  14. You X, Hua C, Li K, et al. Fixed-time leader-following consensus for high-order time-varying nonlinear multiagent systems. IEEE Trans Automat Contr, 2020, 65: 5510–5516

    Article  MathSciNet  MATH  Google Scholar 

  15. Hua C, You X, Guan X. Adaptive leader-following consensus for second-order time-varying nonlinear multiagent systems. IEEE Trans Cybern, 2017, 47: 1532–1539

    Article  Google Scholar 

  16. Su H, Chen M Z Q, Wang X, et al. Semiglobal observer-based leader-following consensus with input saturation. IEEE Trans Ind Electron, 2014, 61: 2842–2850

    Article  Google Scholar 

  17. Dong X, Zhou Y, Ren Z, et al. Time-varying formation tracking for second-order multi-agent systems subjected to switching topologies with application to quadrotor formation flying. IEEE Trans Ind Electron, 2017, 64: 5014–5024

    Article  Google Scholar 

  18. Chen J, Li J, Yuan X. Distributed fuzzy adaptive consensus for high-order multi-agent systems with an imprecise communication topology structure. Fuzzy Sets Syst, 2021, 402: 1–15

    Article  MathSciNet  MATH  Google Scholar 

  19. Chen W, Li X, Ren W, et al. Adaptive consensus of multi-agent systems with unknown identical control directions based on a novel Nussbaum-type function. IEEE Trans Automat Contr, 2014, 59: 1887–1892

    Article  MathSciNet  MATH  Google Scholar 

  20. Li J, Ho D W C, Li J. Distributed adaptive repetitive consensus control framework for uncertain nonlinear leader-follower multi-agent systems. J Franklin Inst, 2015, 352: 5342–5360

    Article  MathSciNet  MATH  Google Scholar 

  21. Yang N, Li J. New distributed adaptive protocols for uncertain nonlinear leader-follower multi-agent systems via a repetitive learning control approach. J Franklin Inst, 2019, 356: 6571–6590

    Article  MathSciNet  MATH  Google Scholar 

  22. Chen J, Li J, Yang N. Globally repetitive learning consensus control of unknown nonlinear multi-agent systems with uncertain time-varying parameters. Appl Math Model, 2021, 89: 348–362

    Article  MathSciNet  MATH  Google Scholar 

  23. Jin X. Adaptive iterative learning control for high-order nonlinear multi-agent systems consensus tracking. Syst Control Lett, 2016, 89: 16–23

    Article  MathSciNet  MATH  Google Scholar 

  24. Shen D, Xu J X. Distributed learning consensus for heterogenous high-order nonlinear multi-agent systems with output constraints. Automatica, 2018, 97: 64–72

    Article  MathSciNet  MATH  Google Scholar 

  25. Wang W, Wen C, Huang J. Distributed adaptive asymptotically consensus tracking control of nonlinear multi-agent systems with unknown parameters and uncertain disturbances. Automatica, 2017, 77: 133–142

    Article  MathSciNet  MATH  Google Scholar 

  26. Liu C L, Liu F. Stationary consensus of heterogeneous multi-agent systems with bounded communication delays. Automatica, 2011, 47: 2130–2133

    Article  MathSciNet  MATH  Google Scholar 

  27. Zheng Y, Wang L. Finite-time consensus of heterogeneous multi-agent systems with and without velocity measurements. Syst Control Lett, 2012, 61: 871–878

    Article  MathSciNet  MATH  Google Scholar 

  28. Yin X, Yue D. Event-triggered tracking control for heterogeneous multi-agent systems with Markov communication delays. J Franklin Inst, 2013, 350: 1312–1334

    Article  MathSciNet  MATH  Google Scholar 

  29. Wen G, Huang J, Wang C, et al. Group consensus control for heterogeneous multi-agent systems with fixed and switching topologies. Int J Control, 2016, 89: 259–269

    Article  MathSciNet  MATH  Google Scholar 

  30. Wen G, Yu Y, Peng Z, et al. Dynamical group consensus of heterogenous multi-agent systems with input time delays. Neurocomputing, 2016, 175: 278–286

    Article  Google Scholar 

  31. Zhao Q, Zheng Y, Zhu Y Consensus of hybrid multi-agent systems with heterogeneous dynamics. Int J Control, 2020, 93: 2848–2858

    Article  MathSciNet  MATH  Google Scholar 

  32. Li X, Shi P, Wang Y Distributed cooperative adaptive tracking control for heterogeneous systems with hybrid nonlinear dynamics. Nonlin Dyn, 2019, 95: 2131–2141

    Article  MATH  Google Scholar 

  33. Li X, Shi P. Cooperative fault-tolerant tracking control of heterogeneous hybrid-order mechanical systems with actuator and amplifier faults. Nonlin Dyn, 2019, 98: 447–462

    Article  Google Scholar 

  34. Li X, Shi P, Wang Y, et al. Cooperative tracking control of heterogeneous mixed-order multiagent systems with higher-order nonlinear dynamics. IEEE Trans Cybern, 2022, 52: 5498–5507

    Article  Google Scholar 

  35. Chen J, Li J. Globally fuzzy leader-follower consensus of mixed-order nonlinear multi-agent systems with partially unknown direction control. Inf Sci, 2020, 523: 184–196

    Article  MathSciNet  MATH  Google Scholar 

  36. Chen J, Li J, Guo Y, et al. Consensus control of mixed-order nonlinear multiagent systems: framework and case study. IEEE Trans Cybern, 2021, doi: https://doi.org/10.1109/TCYB.2021.3100643

  37. Liuzzo S, Marino R, Tomei P. Adaptive learning control of nonlinear systems by output error feedback. IEEE Trans Automat Contr, 2007, 52: 1232–1248

    Article  MathSciNet  MATH  Google Scholar 

  38. Khalil H K. Nonliear Systems. Upper Saddle River: Prentice-Hall, 1996

    Google Scholar 

  39. Chen C, Wen C, Liu Z, et al. Adaptive consensus of nonlinear multi-agent systems with non-identical partially unknown control directions and bounded modelling errors. IEEE Trans Automat Contr, 2017, 62: 4654–4659

    Article  MathSciNet  MATH  Google Scholar 

  40. Li Y, Liu Y, Tong S. Observer-based neuro-adaptive optimized control of strict-feedback nonlinear systems with state constraints. IEEE Trans Neural Netw Learn Syst, 2022, 33: 3131–3145

    Article  MathSciNet  Google Scholar 

  41. Li Y, Zhang J, Liu W, et al. Observer-based adaptive optimized control for stochastic nonlinear systems with input and state constraints. IEEE Trans Neural Netw Learn Syst, 2021, doi: https://doi.org/10.1109/TNNLS.2021.3087796

  42. Xu K, Wang H, Liu X, et al. Adaptive fuzzy fast finite-time tracking control for nonlinear systems in pure-feedback form with unknown disturbance. Complexity, 2020, 2020: 1–11

    Google Scholar 

  43. Wang H, Bai W, Zhao X, et al. Finite-time-prescribed performance-based adaptive fuzzy control for strict-feedback nonlinear systems with dynamic uncertainty and actuator faults. IEEE Trans Cybern, 2022, 52: 6959–6971

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Xidian University, Xi’an, 710071, China

    JiaXi Chen & JunMin Li

  2. School of Aerospace Science and Technology, Xidian University, Xi’an, 710071, China

    WeiSheng Chen

  3. Science and Technology on Antennas and Microwave Laboratory, Xidian University, Xi’an, 710071, China

    Shuai Zhang

Authors
  1. JiaXi Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. WeiSheng Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. JunMin Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Shuai Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to WeiSheng Chen or Shuai Zhang.

Additional information

This work was supported by the National Natural Science Foundation of China (Grant Nos. 62063031, 62106186, 62073254, 62103136), the Fundamental Research Funds for the Central Universities (Grant Nos. XJS18012, QTZX22049, XJS220704, and 20101196862), and the Young Talent Fund of University Association for Science and Technology in Shaanxi, China (Grant No. 20180502).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chen, J., Chen, W., Li, J. et al. Adaptive neural control of nonlinear periodic time-varying parameterized mixed-order multi-agent systems with unknown control coefficients. Sci. China Technol. Sci. 65, 1675–1684 (2022). https://doi.org/10.1007/s11431-021-2056-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11431-021-2056-5

Keywords

Search

Navigation