Skip to main content
SpringerLink
Log in

Three-dimensionally nonlocal tensile nanobars incorporating surface effect: A self-consistent variational and well-posed model

  • Article
  • Published:
Science China Technological Sciences Aims and scope Submit manuscript

Abstract

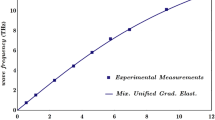
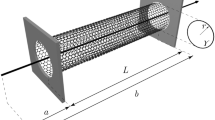
A naturally discrete nanobar implies that the continuum axiom is failed, and its surface-to-volume ratio is very large. The nonlocal theory of elasticity releasing the continuum axiom and the surface theory of elasticity are therefore employed to model tensile nanobars in this work. As commonly believed in the current practice, the axial nonlocal effect is only taken in account to analyze the mechanical behaviors of nanobars, regardless of their three-dimensional inherent atomistic interactions. In this study, a three-dimensional nonlocal constitutive law is developed to model the true nonlocal effect of nanobars, and based on which, a self-consistent variational bar model is proposed. It has been revealed for the first time how both the cross-sectional nonlocal interactions and the axial nonlocality affect the tensile behaviors of nanobars. It is found that the nonlocal influence predicted by the currently axial nonlocal bar model is grossly underestimated. Both the nonlocal cross-sectional and axial interactions become significant when the length-to-height ratio of nanobars is small. If the length-to-height ratio is relatively large (slender bars), the main nonlocal effect stems, however, from the nonlocal cross-sectional effect, rather than the axial nonlocal effect. This work also shows that it is possible to overcome the ill-posed problem of the pure nonlocal integral elasticity by employing both the pure nonlocal integral elasticity and surface elasticity. A well-posed size-dependent governing equation has been established for modeling nanobars under tension, and closed-form solutions are derived for their displacements. Based on the closed-form solutions, the effective elastic modulus is obtained and will be useful for calibrating the physical quantities in the “discretecontinuum” transition region for a span-scale modeling approach. It is shown that the effective elastic modulus may be softening or hardening, depending on the competition between the surface (modulus-hardening) and nonlocal (modulus-softening) effects.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Cowley E R. Lattice dynamics of silicon with empirical many-body potentials. Phys Rev Lett, 1988, 60: 2379–2381

    Article  Google Scholar 

  2. Yakobson B I, Brabec C J, Bernholc J. Nanomechanics of carbon tubes: Instabilities beyond linear response. Phys Rev Lett, 1996, 76: 2511-2514

    Article  Google Scholar 

  3. Admal N C, Tadmor E B. A Unified interpretation of stress in molecular systems. J Elast, 2010, 100: 63–143

    Article  MathSciNet  MATH  Google Scholar 

  4. Duan K, He Y, Li Y, et al. Machine-learning assisted coarse-grained model for epoxies over wide ranges of temperatures and cross-linking degrees. Mater Design, 2019, 183: 108130

    Article  Google Scholar 

  5. Li L, Lin R, Ng T Y. A fractional nonlocal time-space viscoelasticity theory and its applications in structural dynamics. Appl Math Model, 2020, 84: 116–136

    Article  MathSciNet  MATH  Google Scholar 

  6. Eringen A C. Nonlocal Continuum Field Theories. New York: Springer Science & Business Media, 2002

    MATH  Google Scholar 

  7. Aydogdu M. Axial vibration of the nanorods with the nonlocal continuum rod model. Physica E-Low-dimensional Syst NanoStruct, 2009, 41: 861–864

    Article  Google Scholar 

  8. Adhikari S, Murmu T, McCarthy M A. Frequency domain analysis of nonlocal rods embedded in an elastic medium. Physica E-Lowdimensional Syst NanoStruct, 2014, 59: 33–40

    Article  Google Scholar 

  9. Li L, Hu Y, Li X. Longitudinal vibration of size-dependent rods via nonlocal strain gradient theory. Inter J Mech Sci, 2016, 115: 135–144

    Article  Google Scholar 

  10. Angela Pisano A, Fuschi P. Closed form solution for a nonlocal elastic bar in tension. Int J Solids Struct, 2003, 40: 13–23

    Article  MathSciNet  MATH  Google Scholar 

  11. Zhu X, Li L. Closed form solution for a nonlocal strain gradient rod in tension. Int J Eng Sci, 2017, 119: 16–28

    Article  MathSciNet  MATH  Google Scholar 

  12. Zhu X, Li L. Longitudinal and torsional vibrations of size-dependent rods via nonlocal integral elasticity. Int J Mech Sci, 2017, 133: 639–650

    Article  Google Scholar 

  13. Zhu X, Li L. On longitudinal dynamics of nanorods. Int J Eng Sci, 2017, 120: 129–145

    Article  Google Scholar 

  14. Faghidian S A, Mohammad-Sedighi H. Dynamics of nonlocal thick nano-bars. Eng Comput, 2020, doi: https://doi.org/10.1007/s00366-020-01216-3

    Google Scholar 

  15. Li L, Lin R, Hu Y. Cross-section effect on mechanics of nonlocal beams. Archive Appl Mech, 2021, 91: 1541–1556

    Article  Google Scholar 

  16. Eringen A C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J Appl Phys, 1983, 54: 4703–4710

    Article  Google Scholar 

  17. Uzun B, Kafkas U, Yaylı M Ö. Axial dynamic analysis of a bishop nanorod with arbitrary boundary conditions. ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik, 2020, 100: e202000039

    MathSciNet  Google Scholar 

  18. Reddy J N. Nonlocal theories for bending, buckling and vibration of beams. Int J Eng Sci, 2007, 45: 288–307

    Article  MATH  Google Scholar 

  19. Li L, Hu Y. Buckling analysis of size-dependent nonlinear beams based on a nonlocal strain gradient theory. Int J Eng Sci, 2015, 97: 84–94

    Article  MathSciNet  MATH  Google Scholar 

  20. Wu H, Liu H. Nonlinear thermo-mechanical response of temperaturedependent FG sandwich nanobeams with geometric imperfection. Eng Comput, 2020, doi: https://doi.org/10.1007/s00366-020-01005-y

    Google Scholar 

  21. Ghayesh M H, Farajpour A. Nonlinear coupled mechanics of nanotubes incorporating both nonlocal and strain gradient effects. Mech Adv Mater Struct, 2020, 27: 373–382

    Article  Google Scholar 

  22. Civalek Ö, Uzun B, Yaylı M Ö, et al. Size-dependent transverse and longitudinal vibrations of embedded carbon and silica carbide nanotubes by nonlocal finite element method. Eur Phys J Plus, 2020, 135: 381

    Article  Google Scholar 

  23. Tang H, Li L, Hu Y. Coupling effect of thickness and shear deformation on size-dependent bending of micro/nano-scale porous beams. Appl Math Model, 2019, 66: 527–547

    Article  MathSciNet  MATH  Google Scholar 

  24. Shahraki H, Tajmir Riahi H, Izadinia M, et al. Buckling and vibration analysis of FG-CNT-reinforced composite rectangular thick nanoplates resting on Kerr foundation based on nonlocal strain gradient theory. J Vib Control, 2020, 26: 277–305

    Article  MathSciNet  Google Scholar 

  25. Karami B, Shahsavari D, Janghorban M, et al. On the resonance of functionally graded nanoplates using bi-Helmholtz nonlocal strain gradient theory. Int J Eng Sci, 2019, 144: 103143

    Article  MathSciNet  MATH  Google Scholar 

  26. Karami B, Janghorban M. On the mechanics of functionally graded nanoshells. Int J Eng Sci, 2020, 153: 103309

    Article  MathSciNet  MATH  Google Scholar 

  27. Xu X, Karami B, Janghorban M. On the dynamics of nanoshells. Int J Eng Sci, 2021, 158: 103431

    Article  MathSciNet  MATH  Google Scholar 

  28. Gurtin M E, Ian Murdoch A. Surface stress in solids. Int J Solids Struct, 1978, 14: 431–440

    Article  MATH  Google Scholar 

  29. Steigmann D J, Ogden RW. Elastic surface substrate interactions. Proceed R Soc London Ser A, 1999, 455: 437–474

    Article  MathSciNet  MATH  Google Scholar 

  30. Gao X, Huang Z, Qu J, et al. A curvature-dependent interfacial energybased interface stress theory and its applications to nano-structured materials: (I) General theory. J Mech Phys Solids, 2014, 66: 59–77

    Article  MathSciNet  MATH  Google Scholar 

  31. He J, Lilley C M. Surface effect on the elastic behavior of static bending nanowires. Nano Lett, 2008, 8: 1798–1802

    Article  Google Scholar 

  32. Eremeyev V A. On effective properties of materials at the nano- and microscales considering surface effects. Acta Mech, 2016, 227: 29–42

    Article  MathSciNet  MATH  Google Scholar 

  33. Duan H L, Wang J X, Karihaloo B L. Theory of elasticity at the nanoscale. Adv Appl Mech, 2009, 42: 1–68

    Article  Google Scholar 

  34. Kiani K. Free dynamic analysis of functionally graded tapered nanorods via a newly developed nonlocal surface energy-based integrodifferential model. Composite Struct, 2016, 139: 151–166

    Article  Google Scholar 

  35. Kiani K, Żur K K. Vibrations of double-nanorod-systems with defects using nonlocal-integral-surface energy-based formulations. Composite Struct, 2021, 256: 113028

    Article  Google Scholar 

  36. Yuan Y, Xu K, Kiani K. Torsional vibration of nonprismatically nonhomogeneous nanowires with multiple defects: Surface energy-nonlocalintegro-based formulations. Appl Math Model, 2020, 82: 17–44

    Article  MathSciNet  MATH  Google Scholar 

  37. Kiani K, Żur K K. Dynamic behavior of magnetically affected rod-like nanostructures with multiple defects via nonlocal-integral/differentialbased models. Nanomaterials, 2020, 10: 2306

    Article  Google Scholar 

  38. Li L, Lin R, Ng T Y. Contribution of nonlocality to surface elasticity. Int J Eng Sci, 2020, 152: 103311

    Article  MathSciNet  MATH  Google Scholar 

  39. Ruzsicska B P, Jodhan A, Choi H K J, et al. Chemistry of carbynes: Reaction of CF, CCl, and CBr with alkenes. J Am Chem Soc, 1983, 105: 2489–2490

    Article  Google Scholar 

  40. Zhu X, Li L. Twisting statics of functionally graded nanotubes using Eringen’s nonlocal integral model. Composite Struct, 2017, 178: 87–96

    Article  Google Scholar 

  41. Bažant Z P, Jirásek M. Nonlocal integral formulations of plasticity and damage: Survey of progress. J Eng Mech, 2002, 128: 1119–1149

    Google Scholar 

  42. Srinivasa A R, Reddy J N. An overview of theories of continuum mechanics with nonlocal elastic response and a general framework for conservative and dissipative systems. Appl Mech Rev, 2017, 69: 030802

    Article  Google Scholar 

  43. Kiani K. Nonlocal-integro-differential modeling of vibration of elastically supported nanorods. Physica E-Low-dimensional Syst NanoStruct, 2016, 83: 151–163

    Article  Google Scholar 

  44. Fernández-Sáez J, Zaera R, Loya J A, et al. Bending of Euler-Bernoulli beams using Eringen’s integral formulation: A paradox resolved. Int J Eng Sci, 2016, 99: 107–116

    Article  MathSciNet  MATH  Google Scholar 

  45. Eringen A C. Linear theory of nonlocal elasticity and dispersion of plane waves. Int J Eng Sci, 1972, 10: 425–435

    Article  MATH  Google Scholar 

  46. Farajpour A, Howard C Q, Robertson W S P. On size-dependent mechanics of nanoplates. Int J Eng Sci, 2020, 156: 103368

    Article  MathSciNet  MATH  Google Scholar 

  47. Darban H, Luciano R, Caporale A, et al. Higher modes of buckling in shear deformable nanobeams. Int J Eng Sci, 2020, 154: 103338

    Article  MathSciNet  MATH  Google Scholar 

  48. Barretta R, Faghidian S A, de Sciarra F M. A consistent variational formulation of bishop nonlocal rods. Contin Mech Thermodyn, 2020, 32: 1311–1323

    Article  MathSciNet  Google Scholar 

  49. Benvenuti E, Simone A. One-dimensional nonlocal and gradient elasticity: Closed-form solution and size effect. Mech Res Commun, 2013, 48: 46–51

    Article  Google Scholar 

  50. Wang Y B, Zhu X W, Dai H H. Exact solutions for the static bending of Euler-Bernoulli beams using Eringen’s two-phase local/nonlocal model. AIP Adv, 2016, 6: 085114

    Article  Google Scholar 

  51. Polyanin A D, Manzhirov A V. Handbook of Integral Equations. New York: CRC Press, 2008

    Book  MATH  Google Scholar 

  52. Altenbach H, Eremeyev V A, Lebedev L P. On the existence of solution in the linear elasticity with surface stresses. Z angew Math Mech, 2010, 90: 231–240

    Article  MathSciNet  MATH  Google Scholar 

  53. Zhu Y. Mechanics of crystalline nanowires: An experimental perspective. Appl Mech Rev, 2017, 69: 010802

    Article  Google Scholar 

  54. Shen J P, Li C. A semi-continuum-based bending analysis for extremethin micro/nano-beams and new proposal for nonlocal differential constitution. Composite Struct, 2017, 172: 210–220

    Article  Google Scholar 

  55. Li C, Shen Q, Yao L, et al. Lateral bending vibration of nanoscale ultrathin beams using a semi-continuum model. J Comput Theor Nanosci, 2015, 12: 2507–2514

    Article  Google Scholar 

  56. Tang H, Li L, Hu Y, et al. Vibration of nonlocal strain gradient beams incorporating Poisson’s ratio and thickness effects. Thin-Walled Struct, 2019, 137: 377–391

    Article  Google Scholar 

  57. Li C, Zheng Z J, Yu J L, et al. Static analysis of ultra-thin beams based on a semi-continuum model. Acta Mech Sin, 2011, 27: 713–719

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Statistics and Mathematics, Zhongnan University of Economics and Law, Wuhan, 430073, China

    XiaoWu Zhu

  2. State Key Laboratory of Digital Manufacturing Equipment and Technology, School of Mechanical Science and Engineering, Huazhong University of Science and Technology, Wuhan, 430074, China

    Li Li

Authors
  1. XiaoWu Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Li Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Li Li.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhu, X., Li, L. Three-dimensionally nonlocal tensile nanobars incorporating surface effect: A self-consistent variational and well-posed model. Sci. China Technol. Sci. 64, 1–14 (2021). https://doi.org/10.1007/s11431-021-1822-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11431-021-1822-0

Keywords

Search

Navigation