Skip to main content
SpringerLink
Log in

A hybrid method to select morphometric features using tensor completion and F-score rank for gifted children identification

  • Article
  • Published:
Science China Technological Sciences Aims and scope Submit manuscript

Abstract

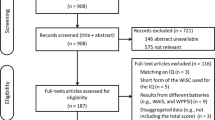
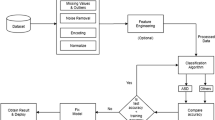
Gifted children are able to learn in a more advanced way than others, probably due to neurophysiological differences in the communication efficiency in neural pathways. Topological features contribute to understanding the correlation between the brain structure and intelligence. Despite decades of neuroscience research using MRI, methods based on brain region connectivity patterns are limited by MRI artifacts, which therefore leads to revisiting MRI morphometric features, with the aim of using them to directly identify gifted children instead of using brain connectivity. However, the small, high-dimensional morphometric feature dataset with outliers makes the task of finding good classification models challenging. To this end, a hybrid method is proposed that combines tensor completion and feature selection methods to handle outliers and then select the discriminative features. The proposed method can achieve a classification accuracy of 93.1%, higher than other existing algorithms, which is thus suitable for the small MRI datasets with outliers in supervised classification scenarios.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Navas-Sánchez F J, Carmona S, Alemán-Gómez Y, et al. Cortical morphometry in frontoparietal and default mode networks in math-gifted adolescents. Hum Brain Mapp, 2016, 37: 1893–1902

    Article  Google Scholar 

  2. Gross M U M. Exceptionally gifted children: Long-term outcomes of academic acceleration and nonacceleration. J Education Gifted, 2006, 29: 404–429

    Article  Google Scholar 

  3. Navas-Sánchez F J, Alemán-Gómez Y, Sánchez-Gonzalez J, et al. White matter microstructure correlates of mathematical giftedness and intelligence quotient. Hum Brain Mapp, 2014, 35: 2619–2631

    Article  Google Scholar 

  4. Hales P W, d’Arco F, Cooper J, et al. Arterial spin labelling and diffusion-weighted imaging in paediatric brain tumours. Neurolmage-Clin, 2019, 22: 101696

    Article  Google Scholar 

  5. Raja R, Rosenberg G, Caprihan A. Review of diffusion MRI studies in chronic white matter diseases. Neurosci Lett, 2019, 694: 198–207

    Article  Google Scholar 

  6. Assaf Y, Johansen-Berg H, Thiebaut de Schotten M. The role of diffusion MRI in neuroscience. NMR Biomed, 2019, 32: e3762

    Article  Google Scholar 

  7. Yun J Y, Boedhoe P S W, Vriend C, et al. Brain structural covariance networks in obsessive-compulsive disorder: A graph analysis from the ENIGMA Consortium. Brain, 2020, 143: 684–700

    Google Scholar 

  8. Qi T, Schaadt G, Cafiero R, et al. The emergence of long-range language network structural covariance and language abilities. NeuroImage, 2019, 191: 36–48

    Article  Google Scholar 

  9. DuPre E, Spreng R N. Structural covariance networks across the life span, from 6 to 94 years of age. Network Neurosci, 2017, 1: 302–323

    Article  Google Scholar 

  10. Walker L, Gozzi M, Lenroot R, et al. Diffusion tensor imaging in young children with autism: Biological effects and potential confounds. Biol Psychiatry, 2012, 72: 1043–1051

    Article  Google Scholar 

  11. Maier-Hein K H, Neher P, Houde J-C, et al. Tractography-based connectomes are dominated by false-positive connections. bioRxiv, 2016, doi: https://doi.org/10.1101/084137

  12. Solé-Casals J, Serra-Grabulosa J M, Romero-Garcia R, et al. Structural brain network of gifted children has a more integrated and versatile topology. Brain Struct Funct, 2019, 224: 2373–2383

    Article  Google Scholar 

  13. Bethlehem R A I, Romero-Garcia R, Mak E, et al. Structural covariance networks in children with autism or ADHD. Cerebral Cortex, 2017, 27: 4267–4276

    Article  Google Scholar 

  14. Seidlitz J, Váša F, Shinn M, et al. Morphometric similarity networks detect microscale cortical organization and predict inter-individual cognitive variation. Neuron, 2018, 97: 231–247.e7

    Article  Google Scholar 

  15. Yang J H, Zhao X L, Ji T Y, et al. Low-rank tensor train for tensor robust principal component analysis. Appl Math Computation, 2020, 367: 124783

    Article  MathSciNet  Google Scholar 

  16. Zhao X L, Xu W H, Jiang T X, et al. Deep plug-and-play prior for low-rank tensor completion. Neurocomputing, 2020, 400: 137–149

    Article  Google Scholar 

  17. Huang H, Liu Y, Liu J, et al. Provable tensor ring completion. Signal Processing, 2020, 171: 107486

    Article  Google Scholar 

  18. Lacroix T, Obozinski G, Usunier N. Tensor decompositions for temporal knowledge base completion. 2020, arXiv: 2004.04926

  19. Lu C, Peng X, Wei Y. Low-rank tensor completion with a new tensor nuclear norm induced by invertible linear transforms. In: Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Long Beach, 2019

  20. Chen Y L, C THsu, Liao H Y M. Simultaneous tensor decomposition and completion using factor priors. IEEE Trans Pattern Anal Mach Intell, 2014, 36: 577–591

    Article  Google Scholar 

  21. Balažević I, Allen C, Hospedales T M. Tucker: Tensor factorization for knowledge graph completion. In: EMNLP-IJCNLP 2019–2019 Conference on Empirical Methods in Natural Language Processing and 9th International Joint Conference on Natural Language Processing, Proceedings of the Conference. Hong Kong, 2020

  22. Najafi M, He L, Yu P S. Outlier-robust multi-aspect streaming tensor completion and factorization. In: IJCAI International Joint Conference on Artificial Intelligence. Macao, 2019

  23. Ko C Y, Batselier K, Daniel L, et al. Fast and accurate tensor completion with total variation regularized tensor trains. IEEE Trans Image Process, 2020, 29: 6918–6931

    Article  MathSciNet  Google Scholar 

  24. Solé-Casals J, Caiafa C F, Zhao Q, et al. Brain-computer interface with corrupted EEG data: A tensor completion approach. Cogn Comput, 2018, 10: 1062–1074

    Article  Google Scholar 

  25. Feng D, Hao J, Zhenglu Y, et al. On the Robustness of EEG Tensor Completion Methods. Sci China Tech Sci, 2021, doi: https://doi.org/10.1007/s11431-020-1839-5

  26. Gárate-Escamila A K, Hajjam El Hassani A, Andrès E. Classification models for heart disease prediction using feature selection and PCA. Inf Med Unlocked, 2020, 19: 100330

    Article  Google Scholar 

  27. Chen Y W, Lin C J. Combining SVMs with various feature selection strategies. In: Guyon I, Nikravesh M, Gunn S, et al. (eds). Feature Extraction. Studies in Fuzziness and Soft Computing. Vol 207. Berlin, Heidelberg: Springer, 2006

    Chapter  Google Scholar 

  28. Tsagris M, Lagani V, Tsamardinos I. Feature selection for high-dimensional temporal data. BMC BioInf, 2018, 19: 17

    Article  Google Scholar 

  29. Ang J C, Mirzal A, Haron H, et al. Supervised, unsupervised, and semi-supervised feature selection: A review on gene selection. IEEE ACM Trans Comput Biol Bioinf, 2016, 13: 971–989

    Article  Google Scholar 

  30. Rouhi A, Nezamabadi-Pour H. Feature selection in high-dimensional data. In: Amini M, ed. Advances in Intelligent Systems and Computing. Vol. 1123. Cham: Springer, 2020. 85–128

    Google Scholar 

  31. Limiñana Gras R M, Bordoy M, Ballesta G J, et al. Creativity, intelectual abilities and response styles: Implications for academic performance in the secondary school. Anales de Psicología/Annals of Psychology, 2010, 26: 212–219

    Google Scholar 

  32. Romero-Garcia R, Atienza M, Clemmensen L H, et al. Effects of network resolution on topological properties of human neocortex. NeuroImage, 2012, 59: 3522–3532

    Article  Google Scholar 

  33. Desikan R S, Ségonne F, Fischl B, et al. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. NeuroImage, 2006, 31: 968–980

    Article  Google Scholar 

  34. Li Z, Sergin N D, Yan H, et al. Tensor completion for weakly-dependent data on graph for metro passenger flow prediction. 2019, arXiv: 1912.05693v1

  35. van den Heuvel M P, Scholtens L H, Feldman Barrett L, et al. Bridging cytoarchitectonics and connectomics in human cerebral cortex. J Neurosci, 2015, 35: 13943–13948

    Article  Google Scholar 

Download references

Author information

Author notes

  1. These authors contributed equally to this work.

Authors and Affiliations

  1. College of Computer Science, Nankai University, Tianjin, 300350, China

    Jin Zhang & TianYi Han

  2. Department of Artificial Intelligence, Nankai University, Tianjin, 300350, China

    Fan Feng, Feng Duan, Cesar F. Caiafa & Jordi Solé-Casals

  3. Computational Engineering Applications Unit, Head Office for Information Systems and Cybersecurity, RIKEN, 351-0198, Saitama, Japan

    Zhe Sun

  4. Instituto Argentino de Radioastronomía—CCT La Plata, CONICET/CIC-PBA/UNLP, 1894, V. Elisa, Argentina

    Cesar F. Caiafa

  5. Department of Psychiatry, University of Cambridge, Cambridge, CB2 0SZ, UK

    Jordi Solé-Casals

  6. Data and Signal Processing Group, University of Vic—Central University of Catalonia, 08500, Vic, Catalonia, Spain

    Jordi Solé-Casals

Authors
  1. Jin Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Fan Feng
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. TianYi Han
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Feng Duan
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Zhe Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Cesar F. Caiafa
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Jordi Solé-Casals
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Feng Duan, Zhe Sun or Jordi Solé-Casals.

Additional information

This work was supported by the National Key R&D Program of China (Grant No. 2017YFE0129700), the National Natural Science Foundation of China (Key Program) (Grant No. 11932013), the National Natural Science Foundation of China (Grant No. 61673224), the Tianjin Natural Science Foundation for Distinguished Young Scholars (Grant No. 18JCJQJC46100), and the Tianjin Science and Technology Plan Project (Grant No. 18ZXJMTG00260). J.S-C. work is also based upon work from COST Action CA18106, supported by COST (European Cooperation in Science and Technology). C.F.C work was supported by grants PICT 2017-3208 and UBACYT 20020170100192BA (Argentina).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, J., Feng, F., Han, T. et al. A hybrid method to select morphometric features using tensor completion and F-score rank for gifted children identification. Sci. China Technol. Sci. 64, 1863–1871 (2021). https://doi.org/10.1007/s11431-020-1876-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11431-020-1876-3

Search

Navigation