Skip to main content
SpringerLink
Log in

Memristor initial-boosted coexisting plane bifurcations and its extreme multi-stability reconstitution in two-memristor-based dynamical system

  • Article
  • Published:
Science China Technological Sciences Aims and scope Submit manuscript

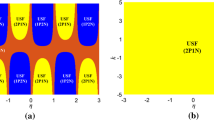
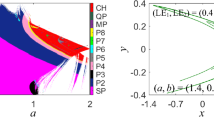
Abstract

Initial-dependent extreme multi-stability and offset-boosted coexisting attractors have been significantly concerned recently. This paper constructs a novel five-dimensional (5-D) two-memristor-based dynamical system by introducing two memristors with cosine memductance into a three-dimensional (3-D) linear autonomous dissipative system. Through theoretical analyses and numerical plots, the memristor initial-boosted coexisting plane bifurcations are found and the memristor initial-dependent extreme multi-stability is revealed in such a two-memristor-based dynamical system with plane equilibrium. Furthermore, a dimensionality reduction model with the determined equilibrium is established via an integral transformation method, upon which the memristor initial-dependent extreme multi-stability is reconstituted theoretically and expounded numerically Finally, physically circuit-implemented PSIM (power simulation) simulations are carried out to validate the plane offset-boosted coexisting behaviors.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Eshraghian K, Kavehei O, Cho K R, et al. Memristive device fundamentals and modeling: Applications to circuits and systems simulation. Proc IEEE, 2012, 100: 1991–2007

    Google Scholar 

  2. Li Q, Hu S, Tang S, et al. Hyperchaos and horseshoe in a 4D memristive system with a line of equilibria and its implementation. Int J Circ Theor Appl, 2014, 42: 1172–1188

    Google Scholar 

  3. Zhou L, Wang C, Zhou L. Generating four-wing hyperchaotic attractor and two-wing, three-wing, and four-wing chaotic attractors in 4D memristive system. Int J Bifurcation Chaos, 2017, 27: 1750027

    MathSciNet  MATH  Google Scholar 

  4. Bao B, Jiang T, Wang G, et al. Two-memristor-based Chua’s hyperchaotic circuit with plane equilibrium and its extreme multi-stability. Nonlinear Dyn, 2017, 89: 1157–1171

    Google Scholar 

  5. Prousalis D A, Volos C K, Stouboulos I N, et al. Hyperchaotic memristive system with hidden attractors and its adaptive control scheme. Nonlinear Dyn, 2017, 90: 1681–1694

    MathSciNet  Google Scholar 

  6. Pham V T, Jafari S, Vaidyanathan S, et al. A novel memristive neural network with hidden attractors and its circuitry implementation. Sci China Tech Sci, 2016, 59: 358–363

    Google Scholar 

  7. Njitacke Z T, Kengne J, Fotsin H B, et al. Coexistence of multiple attractors and crisis route to chaos in a novel memristive diode bidge-based Jerk circuit. Chaos Soliton Fract, 2016, 91: 180–197

    MATH  Google Scholar 

  8. Xu Q, Zhang Q L, Qian H, et al. Crisis-induced coexisting multiple attractors in a second-order nonautonomous memristive diode bridge-based circuit. Int J Circ Theor Appl, 2018, 46: 1917–1927

    Google Scholar 

  9. Corinto F, Forti M. Memristor circuits: Bifurcations without parameters. IEEE Trans Circuits Syst I, 2017, 64: 1540–1551

    Google Scholar 

  10. Chen M, Sun M, Bao H, et al. Flux-charge analysis of two-memristor-based Chua’s circuit: Dimensionality decreasing model for detecting extreme multistability. IEEE Trans Ind Electron, 2019, doi: https://doi.org/10.1109/TIE.2019.2907444

    Google Scholar 

  11. Zhang Y, Liu Z, Wu H, et al. Two-memristor-based chaotic system and its extreme multistability reconstitution via dimensionality reduction analysis. Chaos Soliton Fract, 2019, 127: 354–363

    MathSciNet  Google Scholar 

  12. Bao B C, Shi G D, Xu J P, et al. Dynamics analysis of chaotic circuit with two memristors. Sci China Tech Sci, 2011, 54: 2180–2187

    MATH  Google Scholar 

  13. Ishaq Ahamed A, Lakshmanan M. Nonsmooth bifurcations, transient hyperchaos and hyperchaotic beats in a memristive Murali-Laksh-manan-Chua circuit. Int J Bifurcation Chaos, 2013, 23: 1350098

    MATH  Google Scholar 

  14. Bao B C, Wu P Y, Bao H, et al. Numerical and experimental confirmations of quasi-periodic behavior and chaotic bursting in third-order autonomous memristive oscillator. Chaos Soliton Fract, 2018, 106: 161–170

    MathSciNet  Google Scholar 

  15. Wu H, Ye Y, Chen M, et al. Extremely slow passages in low-pass filter-based memristive oscillator. Nonlinear Dyn, 2019, 97: 2339–2353

    Google Scholar 

  16. Sah M P, Hyongsuk Kim M P, Chua L O. Brains are made of memristors. IEEE Circuits Syst Mag, 2014, 14: 12–36

    Google Scholar 

  17. Ma W, Zidan M A, Lu W D. Neuromorphic computing with memristive devices. Sci China Inf Sci, 2018, 61: 060422

    Google Scholar 

  18. Ma J, Tang J. A review for dynamics in neuron and neuronal network. Nonlinear Dyn, 2017, 89: 1569–1578

    MathSciNet  Google Scholar 

  19. Bao H, Hu A H, Liu W B, et al. Hidden bursting firings and bifurcation mechanisms in memristive neuron model with threshold electromagnetic induction. IEEE Trans Neural Netw Learn Syst, 2019, doi: https://doi.org/10.1109/TNNLS.2019.2905137

  20. Ge M, Jia Y, Xu Y, et al. Mode transition in electrical activities of neuron driven by high and low frequency stimulus in the presence of electromagnetic induction and radiation. Nonlinear Dyn, 2018, 91: 515–523

    Google Scholar 

  21. Bao H, Liu W, Hu A. Coexisting multiple firing patterns in two adjacent neurons coupled by memristive electromagnetic induction. Nonlinear Dyn, 2019, 95: 43–56

    Google Scholar 

  22. Lu L L, Jia Y, Xu Y, et al. Energy dependence on modes of electric activities of neuron driven by different external mixed signals under electromagnetic induction. Sci China Tech Sci, 2019, 62: 427–440

    Google Scholar 

  23. Rajamani V, Kim H, Chua L. Morris-Lecar model of third-order barnacle muscle fiber is made of volatile memristors. Sci China Inf Sci, 2018, 61: 060426

    MathSciNet  Google Scholar 

  24. Hu M, Li H, Chen Y, et al. Memristor crossbar-based neuromorphic computing system: A case study. IEEE Trans Neural Netw Learn Syst, 2014, 25: 1864–1878

    Google Scholar 

  25. Ntinas V, Vourkas I, Abusleme A, et al. Experimental study of artificial neural networks using a digital memristor simulator. IEEE Trans Neural Netw Learn Syst, 2018, 29: 5098–5110

    Google Scholar 

  26. Du L, Cao Z L, Lei Y M, et al. Electrical activities of neural systems exposed to sinusoidal induced electric field with random phase. Sci China Tech Sci, 2019, 62: 1141–1150

    Google Scholar 

  27. Bao B, Hu A, Bao H, et al. Three-dimensional memristive hindmarshrose neuron model with hidden coexisting asymmetric behaviors. Complexity, 2018, 3872573

  28. Lv M, Ma J, Yao Y G, et al. Synchronization and wave propagation in neuronal network under field coupling. Sci China Tech Sci, 2019, 62: 448–457

    Google Scholar 

  29. Parastesh F, Rajagopal K, Alsaadi F E, et al. Birth and death of spiral waves in a network of Hindmarsh-Rose neurons with exponential magnetic flux and excitable media. Appl Math Comput, 2019, 354: 377–384

    MathSciNet  MATH  Google Scholar 

  30. Yan J, Zhang Q, Yin P. RNA editing machinery in plant organelles. Sci China Life Sci, 2018, 61: 162–169

    Google Scholar 

  31. Wu F, Wang C, Jin W, et al. Dynamical responses in a new neuron model subjected to electromagnetic induction and phase noise. Physica A, 2017, 469: 81–88

    MathSciNet  MATH  Google Scholar 

  32. Li C, Min F, Jin Q, et al. Extreme multistability analysis of memristor-based chaotic system and its application in image decryption. AIP Adv, 2017, 7: 125204

    Google Scholar 

  33. Chen M, Sun M, Bao B, et al. Controlling extreme multistability of memristor emulator-based dynamical circuit in flux-charge domain. Nonlinear Dyn, 2018, 91: 1395–1412

    Google Scholar 

  34. Chen M, Feng Y, Bao H, et al. Hybrid state variable incremental integral for reconstructing extreme multistability in memristive jerk system with cubic nonlinearity. Complexity, 2019, 8549472

  35. Jafari S, Ahmadi A, Panahi S, et al. Extreme multi-stability: When imperfection changes quality. Chaos Soliton Fract, 2018, 108: 182–186

    Google Scholar 

  36. Njitacke Z T, Kengne J, Tapche R W, et al. Uncertain destination dynamics of a novel memristive 4D autonomous system. Chaos Soliton Fract, 2018, 107: 177–185

    MathSciNet  MATH  Google Scholar 

  37. Yuan F, Deng Y, Li Y, et al. The amplitude, frequency and parameter space boosting in a memristor-meminductor-based circuit. Nonlinear Dyn, 2019, 96: 389–405

    Google Scholar 

  38. Bao B C, Bao H, Wang N, et al. Hidden extreme multistability in memristive hyperchaotic system. Chaos Soliton Fract, 2017, 94: 102–111

    MathSciNet  MATH  Google Scholar 

  39. Bao H, Liu W, Chen M. Hidden extreme multistability and dimensionality reduction analysis for an improved non-autonomous memristive FitzHugh-Nagumo circuit. Nonlinear Dyn, 2019, 96: 1879–1894

    Google Scholar 

  40. Li C, Sprott J C, Mei Y. An infinite 2-D lattice of strange attractors. Nonlinear Dyn, 2017, 89: 2629–2639

    MathSciNet  Google Scholar 

  41. Li C, Joo-Chen Thio W, Sprott J C, et al. Constructing infinitely many attractors in a programmable chaotic circuit. IEEE Access, 2018, 6: 29003–29012

    Google Scholar 

  42. Li C, Sprott J C. An infinite 3-D quasiperiodic lattice of chaotic attractors. Phys Lett A, 2018, 382: 581–587

    MathSciNet  MATH  Google Scholar 

  43. Li C, Xu Y, Chen G, et al. Conditional symmetry: Bond for attractor growing. Nonlinear Dyn, 2019, 95: 1245–1256

    Google Scholar 

  44. Sun J, Zhao X, Fang J, et al. Autonomous memristor chaotic systems of infinite chaotic attractors and circuitry realization. Nonlinear Dyn, 2018, 94: 2879–2887

    Google Scholar 

  45. Strelioff C C, Hübler A W. Medium-term prediction of chaos. Phys Rev Lett, 2006, 96: 044101

    Google Scholar 

  46. Chen C, Chen J, Bao H, et al. Coexisting multi-stable patterns in memristor synapse-coupled Hopfield neural network with two neurons. Nonlinear Dyn, 2019, 95: 3385–3399

    Google Scholar 

  47. He S, Sun K, Banerjee S. Dynamical properties and complexity in fractional-order diffusionless Lorenz system. Eur Phys J Plus, 2016, 131: 254

    Google Scholar 

  48. Fortuna L, Baglio S, Arena P, et al. Hyperchaos from cellular neural networks. Electron Lett, 1995, 31: 250–251

    Google Scholar 

  49. Caponetto R, Dongola G, Fortuna L, et al. New results on the synthesis of FO-PID controllers. Commun Nonlinear Sci Numer Simul, 2010, 15: 997–1007

    MathSciNet  MATH  Google Scholar 

  50. Wang N, Li C, Bao H, et al. Generating multi-scroll Chua’s attractors via simplified piecewise-linear Chua’s diode. IEEE Trans Circuits Syst I, 2019, doi: https://doi.org/10.1109/TCSI.2019.2933365

  51. Buscarino A, Fortuna L, Frasca M. Experimental robust synchronization of hyperchaotic circuits. Physica D-Nonlinear Phenomena, 2009, 238: 1917–1922

    MATH  Google Scholar 

  52. Bao H, Wang N, Bao B, et al. Initial condition-dependent dynamics and transient period in memristor-based hypogenetic jerk system with four line equilibria. Commun Nonlinear Sci Numer Simul, 2018, 57: 264–275

    MathSciNet  Google Scholar 

  53. Hua Z, Zhou Y, Bao B C. Two-dimensional sine chaotification system with hardware implementation. IEEE Trans Ind Inf, 2019, doi: https://doi.org/10.1109/TII.2019.2923553

  54. Li C, Lin D, Lu J, et al. Cryptanalyzing an image encryption algorithm based on autoblocking and electrocardiography. IEEE MultiMedia, 2018, 25: 46–56

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Information Science and Engineering, Changzhou University, Changzhou, 213164, China

    Han Bao, Mo Chen, HuaGan Wu & BoCheng Bao

Authors
  1. Han Bao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mo Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. HuaGan Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. BoCheng Bao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to BoCheng Bao.

Additional information

This work was supported by the National Natural Science Foundation of China (Grant Nos. 51777016, 51607013, 61601062 & 61801054).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bao, H., Chen, M., Wu, H. et al. Memristor initial-boosted coexisting plane bifurcations and its extreme multi-stability reconstitution in two-memristor-based dynamical system. Sci. China Technol. Sci. 63, 603–613 (2020). https://doi.org/10.1007/s11431-019-1450-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11431-019-1450-6

Keywords

Search

Navigation