Abstract
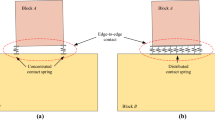
Contact detection between interacting blocks is of great importance to discontinuity-based numerical methods, such as DDA, DEM, and NMM. A rigorous contact theory is a prerequisite to describing the interactions of multiple blocks. Currently, the penalty method, in which mathematical springs with high stiffness values are employed, is always used to calculate the contact forces. High stiffness values may cause numerical oscillations and limit the time step. Furthermore, their values are difficult to identify. The intention of this study is to present a two-scale contact model for the calculation of forces between colliding blocks. In this new model, a calculation step taken from the moment of contact will be divided into two time stages: the free motion time stage and the contact time stage. Actually, these two time stages correspond to two real physical processes. Based on this, we present a new numerical model that is intended to be more precise and useful in calculating the contact forces without mathematical springs. The propagation of the elastic wave during collision is of a characteristic length, which determines the volume of material involved in the contact force calculation. In conventional contact models, this range is always regarded as the length of one element, which may lead to an inaccurate calculation of contact forces. In fact, the real scale of this range is smaller than the length of a single element, and subdivided elements, which are refined according to the characteristic length and are presented in the new contact model.
Similar content being viewed by others
References
Cundall P A. Formulation of a three-dimensional distinct element model—Part I. A scheme to detect and represent contacts in a system composed of many polyhedral blocks. Int J Rock Mech Min, 1988; 25: 107–116
Hart R, Cundall P A, Lemos J. Formulation of a three-dimensional distinct element model—Part II. Mechanical calculations for motion and interaction of a system composed of many polyhedral blocks. Int J Rock Mech Min, 1988; 25: 117–125
Williams J R, O’Connor R. A linear complexity intersection algorithm for discrete element simulation of arbitrary geometries. Eng Comput, 1995; 12: 185–201
Shi G H. Discontinuous deformation analysis—A new numerical model for the statics and dynamics of block systems. Dissertation of Doctor Degree. Dept Civ Eng, UC Berkeley, 1988
Wu J H, Ohnishi Y, Shi G H, et al. Theory of three-dimensional discontinuous deformation analysis and its application to a slope toppling at Amatoribashi, Japan. Int J Geomechanics, 2005; 5: 179–195
Ning Y, Yang J, An X, et al. Modelling rock fracturing and blast-induced rock mass failure via advanced discretisation within the discontinuous deformation analysis framework. Comput Geotech, 2011; 38: 40–49
Beyabanaki S A R, Jafari A, Biabanaki S O R, et al. Nodal-based three-dimensional discontinuous deformation analysis (3-D DDA). Comput Geotech, 2009; 36: 359–372
Munjiza A, Owen D R J, Bicanic N. A combined finite-discrete element method in transient dynamics of fracturing solids. Eng Computation, 1995; 12: 145–174
Munjiza A, Andrews K R F. Penalty function method for combined finite-discrete element systems comprising large number of separate bodies. Int J Numer Meth Eng, 2000; 49: 1377–1396
Shi G H. Manifold method of material analysis. In: Proceedings of the Trans Ninth Army Conference on Applied Mathematics and Computing, Minneapolis, 1991. 57–76
Wu Z, Wong L N Y. Frictional crack initiation and propagation analysis using the numerical manifold method. Comput Geotech, 2012; 39: 38–53
Lankarani H M, Nikravesh P E. A contact force model with hysteresis damping for impact analysis of multibody systems. J Mech Design, 1990; 112: 369–376
Lankarani H M, Nikravesh P E. Continuous contact force models for impact analysis in multibody systems. Nonlinear Dynam, 1994; 5: 193–207
He L, An X M, Ma G W, et al. Development of three-dimensional numerical manifold method for jointed rock slope stability analysis. Int J Rock Mech Min, 2013; 64: 22–35
Wu J H. New edge-to-edge contact calculating algorithm in threedimensional discrete numerical analysis. Adv Eng Softw, 2008; 39: 15–24
Beyabanaki S A R, Mikola R G, Hatami K. Three-dimensional discontinuous deformation analysis (3-D DDA) using a new contact resolution algorithm. Comput Geotech, 2008; 35: 346–356
Yeung M R, Jiang Q H, Sun N. A model of edge-to-edge contact for three-dimensional discontinuous deformation analysis. Comput Geotech, 2007; 34: 175–186
Jing L. A review of techniques, advances and outstanding issues in numerical modelling for rock mechanics and rock engineering. Int J Rock Mech Min, 2003; 40: 283–353
Goodman R E, Taylor R L, Brekke T. A model for the mechanics of jointed rock. J Soil Mech Foundations Division, ASCE, 1968; 94: 637–659
Zhou D, Li S H, Zhang Q B, et al. Structure layer model in continuum- discontinuum element method. In: Proceedings of the 6th International Conference on Discrete Element Methods and Related Techniques, Colorado, 2013. 445–450
Wang J, Li S H, Feng C. A shrunken edge algorithm for contact detection between convex polyhedral blocks. Comput Geotech, 2014; 63: 315–330
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Li, S., Tang, D. & Wang, J. A two-scale contact model for collisions between blocks in CDEM. Sci. China Technol. Sci. 58, 1596–1603 (2015). https://doi.org/10.1007/s11431-015-5902-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11431-015-5902-4