Skip to main content
SpringerLink
Log in

Super-harmonic responses analysis for a cracked rotor system considering inertial excitation

  • Article
  • Published:
Science China Technological Sciences Aims and scope Submit manuscript

Abstract

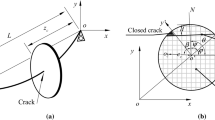
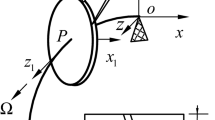
In this paper, an investigation on the nonlinear vibration, especially on the super-harmonic resonances, in a cracked rotor system is carried out to provide a novel idea for the detection of crack faults in rotor systems. The motion equations of the system are formulated with the consideration of the additional excitation from an inertial environment as well as the forced excitation of the rotor unbalance. By using the harmonic balance method, the analytical solutions of the equations with four orders of harmonic exponents are obtained to analyze the nonlinear response of the system. Then through numerical calculations, the vibration responses affected by system parameters including the inertial excitation, the forced excitation, the crack and damping factors are investigated in detail. The results show that the occurrence of the super-harmonic resonances of the rotor system is due to the interaction between crack breathing and the inertial excitation. Correspondingly, the super-harmonic responses are significantly affected by the inertial excitation and the crack stiffness (or depth). The rotor unbalance, however, does not make apparent effects on the super-harmonic responses. Consequently, the super-harmonic resonances peaks can be viewed as an identification signal of the crack fault due to the application of the inertial excitation. By utilizing the inertial excitation, the super-harmonic response signals in rotor systems with early crack faults can be amplified and detected more easily.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Chen Y S, Zhang H B. Review and prospect on the research of dynamics of the aero-engine system. Acta Aeronautica et Astronautica Sinica, 2011, 32: 1371–1391

    Google Scholar 

  2. Chen Z J, Zheng J, Zhang S Y. Finite element modeling of heating phenomena of cracks excited by high-intensity ultrasonic pulses. Chin Phys B, 2010, 19: 118104

    Article  Google Scholar 

  3. Wauer J. Dynamics of cracked rotors: Literature survey. Appl Mech Rev, 1990, 43: 13–17

    Article  Google Scholar 

  4. Gasch R. A survey of the dynamic behaviour of a simple rotating shaft with a transverse crack. J Sound Vib, 1993, 160: 313–332

    Article  MATH  Google Scholar 

  5. Dimarogonas A. Vibration of cracked structures: A state of the art review. Eng Fract Mech, 1996, 55: 831–857

    Article  Google Scholar 

  6. Pennacchi P, Bachschmid N, Vania A. A model-based identification method of transverse cracks in rotating shafts suitable for industrial machines. Mech Syst Signal Pr, 2006, 20: 2112–2147

    Article  Google Scholar 

  7. Sekhar A S. Model-based identification of two cracks in a rotor system. Mech Syst Signal Pr, 2004, 18: 977–983

    Article  Google Scholar 

  8. Ishida Y, Inoue T. Detection of a rotor crack using a harmonic excitation and nonlinear vibration analysis. J Vib Acoust, 2006, 128: 741–749

    Article  Google Scholar 

  9. Sinou J J. Detection of cracks in rotor based on the 2× and 3× superharmonic frequency components and the crack-unbalance interactions. Commun Nonlinear Sci Numer Simulat, 2008, 13: 2024–2040

    Article  Google Scholar 

  10. AL-Shudeifat M A, Butcher E A, Stern C R. General harmonic balance solution of a cracked rotor-bearing-disk system for harmonic and sub-harmonic analysis: Analytical and experimental approach. Int J Eng Sci, 2010, 48: 921–935

    Article  Google Scholar 

  11. Sekhar A S. On-line rotor fault identification by combined model and signal-based approach. Noise Vib Worldwide, 2004, 35: 16–30

    Article  Google Scholar 

  12. Dong H B, Chen X F, Li B, et al. Rotor crack detection based on high-precision modal parameter identification method and wavelet finite element model. Mech Syst Signal Pr, 2009, 23: 869–883

    Article  Google Scholar 

  13. Ramesh Babu T, Srikanth S, Sekhar A S. Hilbert-Huang transform for detection and monitoring of crack in a transient rotor. Mech Syst Signal Pr, 2008, 22: 905–914

    Article  Google Scholar 

  14. Deng X, Wang Q. Crack detection using spatial measurements and wavelets. Int J Fract, 1998, 91: 23–28

    Article  Google Scholar 

  15. Peng Z K, Chu F L. Application of the wavelet transform in machine condition monitoring and fault diagnostics: a review with bibliography. Mech Syst Signal Pr, 2004, 18: 199–221

    Article  Google Scholar 

  16. Sekhar A S. Detection and monitoring of crack in a coast-down rotor supported on fluid film bearings. Tribol Int, 2004, 37: 279–287

    Article  Google Scholar 

  17. Darpe A K. A novel way to detect transverse surface crack in a rotating shaft. J Sound Vib, 2007, 305: 151–171

    Article  Google Scholar 

  18. Mohammed A A, Neilson R D, Deans W F, et al. Crack detection in a rotating shaft using artificial neural networks and PSD characterization. Meccanica, 2014, 49: 255–266

    Article  MATH  Google Scholar 

  19. Zhang C L, Li B, Yang Z B, et al. Crack location identification of rotating rotor systems using operating deflection shape data. Sci China Tech Sci, 2013, 56: 1723–1732

    Article  MathSciNet  Google Scholar 

  20. Zhang L, Zhang Y, Liu X Z, et al. Multi-crack imaging using nonclassical nonlinear acoustic method. Chin Phys B, 2014, 23: 104301

    Article  Google Scholar 

  21. Sekhar A S. Multiple cracks effects and identification. Mech Syst Signal Pr, 2008, 22: 845–878

    Article  Google Scholar 

  22. Machorro-Lopez J M, Adams D E, Gomez-Mancilla J C, et al. Identification of damaged shafts using active sensing–Simulation and experimentation. J Sound Vib, 2009, 327: 368–390

    Article  Google Scholar 

  23. Wang R X, Jin Y, Xu M Q. Approach of fault diagnosis based on similarity degree matching distance function. Sci China Tech Sci, 2013, 56: 2709–2720

    Article  Google Scholar 

  24. Chen B Q, Zhang Z S, Zi Y Y, et al. A pseudo wavelet system-based vibration signature extracting method for rotating machinery fault detection. Sci China Tech Sci, 2013, 56: 1294–1306

    Google Scholar 

  25. Zhang X F, Hu N Q, Hu L, et al. Multi-scale bistable stochastic resonance array: A novel weak signal detection method and application in machine fault diagnosis. Sci China Tech Sci, 2013, 56: 2115–2123

    Article  Google Scholar 

  26. Lin F S, Meng G. Study on the dynamics of a rotor in a maneuvering aircraft. J Vib Acoust, 2003, 125: 324–327

    Article  Google Scholar 

  27. Lin F S, Meng G, Eric H. Nonlinear dynamics of a cracked rotor in a maneuvering aircraft. Appl Math Mech-Eng, 2004, 25: 1139–1150

    Article  MATH  Google Scholar 

  28. Hou L, Chen Y S, Cao Q J. Nonlinear vibration phenomenon of an aircraft rub-impact rotor system due to hovering flight. Commun Nonlinear Sci Numer Simulat, 2014, 19: 286–297

    Article  MathSciNet  Google Scholar 

  29. Hou L, Chen Y S. Analysis of 1/2 sub-harmonic resonance in a maneuvering rotor system. Sci China Tech Sci, 2014, 57: 203–209

    Article  Google Scholar 

  30. Yang Y F, Ren X M, Qin W Y. Study of Nonlinear response of cracked jeffcott rotor in hovering state (in Chinese). J Aero Power, 2007, 22: 1007–1012

    Google Scholar 

  31. Yang Y F, Ren X M, Qin W Y, et al. Analysis on the nonlinear response of cracked rotor in hover flight. Nonlinear Dyn, 2010, 61: 183–192

    Article  MATH  Google Scholar 

  32. Duchemin M, Berlioz A, Ferraris G. Dynamic behavior and stability of a rotor under base excitation. J Vib Acoust, 2006, 128: 576–585

    Article  Google Scholar 

  33. Driot N, Lamarque C H, Berlioz A. Theoretical and experimental analysis of a base-excited rotor. J Comput Nonlin Dyn, 2006, 1: 257–263

    Article  Google Scholar 

  34. Doughty S. Response of single degree of freedom mechanisms to base excitation. Mech Mach Theory, 2001, 36: 833–842

    Article  MATH  Google Scholar 

  35. Lee A S, Kim B O, Kim Y C. A finite element transient response analysis method of a rotor-bearing system to base shock excitations using the state-space Newmark scheme and comparisons with experiments. J Sound Vib, 2006, 297: 595–615

    Article  Google Scholar 

  36. El-Saeidy F M A, Sticher F. Dynamics of a rigid rotor linear/nonlinear bearings system subject to rotating unbalance and base excitations. J Vib Control, 2010, 16: 403–438

    Article  MATH  Google Scholar 

  37. Han Q K, Chu F L. Dynamic response of cracked rotor-bearing system under time-dependent base movements. J Sound Vib, 2013, 332: 6847–6870

    Article  Google Scholar 

  38. Hou L, Chen Y S, Li Z G. Constant-excitation caused response in a class of parametrically excited systems with two degrees of freedom. Acta Phys Sin, 2014, 63: 134501

    Google Scholar 

  39. Xue S M, Cao J Y, Lin J, et al. Influence of fractional order damping on nonlinear dynamics of cracked rotor. J Xi’an Jiaotong Univ, 2012, 46: 76–80

    MathSciNet  Google Scholar 

  40. Zhu C, Robb D, Ewins D. The dynamics of a cracked rotor with an active magnetic bearing. J Sound Vib, 2003, 265: 469–487

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Astronautics, Harbin Institute of Technology, Harbin, 150001, China

    Lei Hou & YuShu Chen

Authors
  1. Lei Hou
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. YuShu Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Lei Hou.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hou, L., Chen, Y. Super-harmonic responses analysis for a cracked rotor system considering inertial excitation. Sci. China Technol. Sci. 58, 1924–1934 (2015). https://doi.org/10.1007/s11431-015-5850-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11431-015-5850-z

Keywords

Search

Navigation