Skip to main content
SpringerLink
Log in

Inner wall running state monitoring for the main pipe of nuclear power

  • Published:
Science China Technological Sciences Aims and scope Submit manuscript

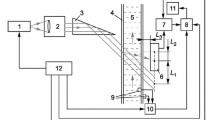
Abstract

The heat conduction equation is solved in this paper under specific boundary conditions. The coefficients of the obtained distribution equation are simplified with the piecewise integral method. Then the associated model for the cylindrical thermal equipment is established. The relationship of the surface temperatures, the material properties and the inner wall state of the cylindrical thermal equipment is described in the associated model. This model is applied to the inner wall running state monitoring of the main pipe. A multi-channel distributed optical fiber temperature measurement system is designed to acquire the external surface temperatures of the main pipe. Then the associated model can be used to analyze the surface temperature data of the main pipe. The location and the physical dimension of the inner wall defect can be got. Therefore, the inner wall defect monitoring of the main pipe can be realized. The feasibility of this method is verified by experiment. This method also provides a theoretical basis for the real-time monitoring of the main pipe’s internal state.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

R 0 :

outer wall radius of the cylinder

L :

axial length of the cylinder

T ∞ :

ambient temperature

T 0 :

inner wall temperature of the cylinder

r :

any point radius within the cylinder

l :

any point axial length within the cylinder

T :

any point temperature within the cylinder

ξ=l/R 0 :

dimensionless axial length

Θ=(T-T)/(T 0-T ∞):

dimensionless temperature

φ :

defect azimuth angle

ρ=r/R 0 :

dimensionless radius

k :

coefficient of heat conduction

h ∞ :

convective heat transfer coefficient of the outside surface

B i∞ = R 0 h ∞/k :

Biot number

References

  1. Kassab A J, Hsieh C K. Solution of the inverse geometric problem for the detection of subsurface cavities by the IR-CAT method. Rev Sci Instrum, 1997, 58(1): 33–65

    Google Scholar 

  2. Sahnoun S, Belattar S. Thermal non destructive testing study of a circular defect in plane structure. British J NDT, 2003, 8 (08): 115–121

    Google Scholar 

  3. Huang C H, Chaing M T. A three-dimensional inverse geometry problem in identifying irregular boundary configurations. Int J Therm Sci, 2009, 48(3): 502–513

    Article  Google Scholar 

  4. Sakagami T, Kubo S. Applications of pulse heating thermography and lock-in theromography to quantitative nondestructive evaluations. Infrared PhysTechnol, 2002, 43(3–5): 211–218

    Article  Google Scholar 

  5. Chen C H, Su C R. Inverse estimation for temperatures of outer surface and geometry of inner surface of furnace with two layer walls. Energy Conver Manag, 2008, 49: 301–310

    Article  Google Scholar 

  6. Gou X L, Zhang J T, Wang G J. Defects detection in the inner surface of pipes based on inverse heat conduction problem (in Chinese). J Chongqing Univ, 2010, 33(2): 42–46

    Google Scholar 

  7. Fan C L, Sun F R, Yang L. Algorithm for solution of inverse geometry problem (in Chinese). CIESC J, 2010, 61(11): 2783–2788

    Google Scholar 

  8. Feng L C, Tao N, Xu C. Lock-in thermography and its application in nondestructive evaluation (in Chinese). Infrared Laser Eng, 2010, 39(6): 1120–1123

    Google Scholar 

  9. Wang Q X, Song L M, Yang Z K. Solving process of three dimension cylindrical system with infrared CAT (in Chinese). Energy Metallurg Indus, 1995, 3(14): 45–49

    Google Scholar 

  10. Guan R H, Yu H. Feasibility to the infrared thermo-diagnosis of the defects in the inner wall of three dimensional cylinder-shaped equipment by means of numerical experiment (in Chinese). Laser and Infrared, 2002, 32(1): 37–39

    Google Scholar 

  11. Kang W X. Infrared therm-diagnosis to internal condition of the double-layer hollow cylinder-shaped heat equipment (in Chinese). Laser and Infrared, 2009, 39(10): 68–69

    Google Scholar 

  12. Ozisik M N. Heat Conduction. 2nd Revised ed. New York: John Wiley, 1993

    Google Scholar 

  13. Tian L P. Mathematical Physics Equation and Its Inverse Problem Research (in Chinese). Beijing: China Machine Press, 2010

    Google Scholar 

  14. Liu H L, Zhuang S L, Zhang Z X. The dynamic base matching method to increase the stability of distributed optical fiber temperature sensors (in Chinese). Proc SPIE, 2002, 4920: 295–298

    Article  Google Scholar 

  15. Crickmore R I, Gunning M J, Dakin J P. Beat frequency measurement system for multiple dual polarization fiber DFB lasers. Sensors J, 2003, 3(1): 115–120

    Article  Google Scholar 

  16. Zhou X J, Du D, Gong J J. Study on spatial resolution of polarized-modes coupling distributed fiber optic sensor (in Chinese). Acta Phys in, 2005, 54(5): 2106–2110

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Electrical Engineering, Yanshan University, Qinhuangdao, 066004, China

    YuCun Zhang, Shan Zhou & XianBin Fu

Authors
  1. YuCun Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shan Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. XianBin Fu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shan Zhou.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zhang, Y., Zhou, S. & Fu, X. Inner wall running state monitoring for the main pipe of nuclear power. Sci. China Technol. Sci. 56, 2606–2614 (2013). https://doi.org/10.1007/s11431-013-5332-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11431-013-5332-0

Keywords

Search

Navigation