Skip to main content
SpringerLink
Log in

Noise reduction method for nonlinear signal based on maximum variance unfolding and its application to fault diagnosis

  • Published:
Science China Technological Sciences Aims and scope Submit manuscript

Abstract

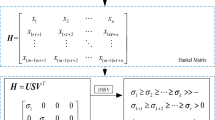
A new noise reduction method for nonlinear signal based on maximum variance unfolding (MVU) is proposed. The noisy signal is firstly embedded into a high-dimensional phase space based on phase space reconstruction theory, and then the manifold learning algorithm MVU is used to perform nonlinear dimensionality reduction on the data of phase space in order to separate low-dimensional manifold representing the attractor from noise subspace. Finally, the noise-reduced signal is obtained through reconstructing the low-dimensional manifold. The simulation results of Lorenz system show that the proposed MVU-based noise reduction method outperforms the KPCA-based method and has the advantages of simple parameter estimation and low parameter sensitivity. The proposed method is applied to fault detection of a vibration signal from rotor-stator of aero engine with slight rubbing fault. The denoised results show that the slight rubbing features overwhelmed by noise can be effectively extracted by the proposed noise reduction method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Hegger R, Kantz H, Matassini L. Noise reduction for human speech signals by local projections in embedding spaces. Circ Syst I: Fund Theory Appl, 2001, 48: 1454–1461

    Article  Google Scholar 

  2. Shin K, Hammond J K, White P R. Iterative SVD method for noise reduction of low dimensional chaotic time series. Mech Syst Sig Proc, 1999, 13: 115–124

    Article  Google Scholar 

  3. Mika S, Schölkopf B, Smola A, et al. Kernel PCA and denoising in feature spaces. Adv Neural Inf Proc Syst, NIPS11, 2000. 11

  4. Gruber P, Stadlthanner K, Böhm M, et al. Denoising using local projective subspace methods. Neurocomput, 2006, 69: 1485–1501

    Article  Google Scholar 

  5. Tenenbaum J B, Silva V D, Langford J C. A global geometric framework for nonlinear dimensionality reduction. Science, 2000, 290: 2319–2323

    Article  Google Scholar 

  6. Roweis S T, Saul L K. Nonlinear dimensionality reduction by locally linear embedding. Science, 2000, 290: 2323–2326

    Article  Google Scholar 

  7. Belkin M, Niyogi P. Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comp, 2003, 15: 1373–1396

    Article  MATH  Google Scholar 

  8. Weinberger K, Saul L. Unsupervised learning of image manifolds by semidefinite programming. Int J Comp Vision, 2006, 70: 11–90

    Article  Google Scholar 

  9. Sturm J F. Using sedumi 1.02, a matlab toolbox for optimization over symmetric cones. Optim Method Softw, 1999, 11: 625–653

    Article  MathSciNet  Google Scholar 

  10. Borchers B. Csdp: A C library for semidefinite programming. Optim Method Softw, 1999, 11: 613–623

    Article  MathSciNet  Google Scholar 

  11. Kostelich E J, Thomas S. Noise reduction in chaotic time series data: A survey of common methods. Phys Rev E, 1993, 48: 1752–1763

    Article  MathSciNet  Google Scholar 

  12. Fan J, Gijbels I. Local Polynomial Modeling and its Applications. London: Chapman and Hall, 1996. 84–87

    Google Scholar 

  13. Lee J M, Yoo C K, Choi S W, et al. Nonlinear process monitoring using kernel principal component analysis. Chem Eng Sci, 2004, 59: 223–234

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Airborne Vehicle Engineering, Naval Aeronautical Engineering Institute, Yantai, 264001, China

    Yun Zhang & BenWei Li

Authors
  1. Yun Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. BenWei Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yun Zhang.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zhang, Y., Li, B. Noise reduction method for nonlinear signal based on maximum variance unfolding and its application to fault diagnosis. Sci. China Technol. Sci. 53, 2122–2128 (2010). https://doi.org/10.1007/s11431-009-3172-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11431-009-3172-8

Keywords

Search

Navigation