Skip to main content
SpringerLink
Log in

Bifurcation and chaos of the bladed overhang rotor system with squeeze film dampers

  • Published:
Science in China Series E: Technological Sciences Aims and scope Submit manuscript

Abstract

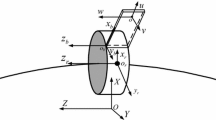
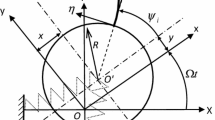
To study the nonlinear dynamic behavior of the bladed overhang rotor system with squeeze film damper (SFD), a blade-overhang rotor-SFD model is formulated using the lumped mass method and the Lagrange approach. The cavitated short bearing model is employed to describe the nonlinear oil force of the SFD. To reduce the scale of the nonlinear coupling system, a set of orthogonal transformations is employed to decouple the one nodal diameter equations of blades, which are coupled with the dynamical equations of the rotor, with other equations of blades. In this way, the original system with 16+4n (n≥3) degrees of freedom (DoF) is reduced to a system with 24 DoF only. Then the parametric excitation terms in the blade-overhang rotor-SFD model are simplified in terms of periodic transformations. The coupling equations are numerically solved and the solutions are used to analyze the dynamic behavior of the system in terms of the bifurcation diagram, whirl orbit, Poincaré map and spectrum plot. A variety of motion types are found such as multi-periodic, quasi-periodic, and chaotic motions. Moreover, the typical nonlinear dynamic evolutions including the periodic-doubling bifurcation and reverse bifurcation are noted. It is noticed that there exist apparent differences in the dynamic behavior between the blade-overhang rotor-SFD models without and with considering the effect of blades.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Crawley E F, Ducharme E H, Mokadam D R. Analytical and experimental investigation of the coupled bladed disk-shaft whirl of a cantilevered turbofan. J Eng Gas Turb Power, 1986, 108(4): 567–576

    Article  Google Scholar 

  2. Chun S B, Lee C W. Vibration analysis of shaft-bladed disk system by using substructure synthesis and assumed modes method. J Sound Vib, 1996, 189(5): 587–608

    Article  Google Scholar 

  3. Zhang J, Liu X P. Principle and Numerical Methods of Modal Analysis to Turbomachines. Beijing: National Defence and Industry Press, 2001

    Google Scholar 

  4. Lee C W, Jia H S, Kim C S, et al. Tuning of simulated natural frequencies for a flexible shaft-multiple flexible disk system. J Sound Vib, 1997, 207(4): 435–451

    Article  Google Scholar 

  5. Chatelet E, D’Ambrosio F, Jacquet-Richardet G. Toward global modeling approaches for dynamic analyses of rotating assemblies of turbomachines. J Sound Vib, 2005, 282(1): 163–178

    Article  Google Scholar 

  6. Genta G. On the stability of rotating blade arrays. J Sound Vib, 2004, 273(7): 805–836

    Article  Google Scholar 

  7. Lesaffre N, Sinou J J, Thouverez F. Contact analysis of a flexible bladed-rotor. Euro J of Mech A/Solids, 2007, 26(4): 541–557

    Article  MATH  Google Scholar 

  8. Sinha S K. Dynamic characteristics of a flexible bladed-rotor with coulomb damping due to tip-rub. J Sound Vib, 2004, 273(7): 875–919

    Article  Google Scholar 

  9. Inayat-Hussain J I, Kanki H, Mureithi N W. Stability and bifurcation of a rigid rotor in cavitated squeeze-film dampers without centering springs. Trib Int, 2001, 34(5): 689–702

    Article  Google Scholar 

  10. Inayat-Hussain J I, Kanki H, Mureithi N W. Chaos in the unbalance response of a rigid rotor in cavitated squeeze-film dampers without centering springs. Chaos Solitons Fract, 2002, 13(8): 929–945

    Article  MATH  Google Scholar 

  11. Inayat-Hussain J I, Kanki H, Mureithi N W. On the bifurcation of a rigid rotor response in squeeze-film dampers. J Fluids Struct, 2003, 17(3): 433–459

    Article  Google Scholar 

  12. Inayat-Hussain J I, Mureithi N W. Transitions to chaos in squeeze-film dampers. Commun in Nonlinear Sci Num Sim, 2006, 11(6): 721–744

    Article  MATH  Google Scholar 

  13. Inayat-Hussain J I. Bifurcations of a flexible rotor response in squeeze-film dampers without centering springs. Chaos Solitons Fract, 2005, 24(4): 583–596

    Article  MATH  Google Scholar 

  14. Rezvani M A, Hahn E J. An experimental evaluation of squeeze film dampers without centralizing springs. Trib Int, 1996, 29(1): 51–59

    Article  Google Scholar 

  15. Wang L G, Cao D Q. Hu C, et al. Effect of the blade vibration on the dynamic behaviors of a rotor-bearing system. J Harbin Eng Univ, 2007, 28(2): 320–325

    Google Scholar 

  16. Zhong Y E, He Y Z, Wang Z, et al. Rotordynamics. Beijing: Tsinghua University Press, 1987

    Google Scholar 

  17. Kim H S. Cho M, Song S J. Stability analysis of a turbine rotor system with Alford forces. J Sound Vib, 2003, 260(1): 167–182

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Astronautics, Harbin Institute of Technology, Harbin, 150001, China

    DengQing Cao, LiGang Wang, YuShu Chen & WenHu Huang

Authors
  1. DengQing Cao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. LiGang Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. YuShu Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. WenHu Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to DengQing Cao.

Additional information

Supported by the National Natural Science Foundation of China (Grant No. 10632040), the Natural Science Foundation of Hei-Long-Jiang Province of China (Grant No. ZJG0704), and the Harbin Science & Technology Innovative Foundation of China (Grant No. 2007RFLXG009)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Cao, D., Wang, L., Chen, Y. et al. Bifurcation and chaos of the bladed overhang rotor system with squeeze film dampers. Sci. China Ser. E-Technol. Sci. 52, 709–720 (2009). https://doi.org/10.1007/s11431-009-0039-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11431-009-0039-y

Keyword

Search

Navigation