Skip to main content
SpringerLink
Log in

On the tension necking of copper single crystal specimen under slip deformation mechanism

  • Published:
Science in China Series E: Technological Sciences Aims and scope Submit manuscript

Abstract

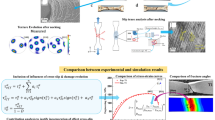
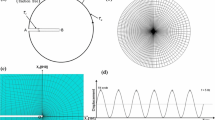
The tension necking of FCC copper single crystal specimen with a square cross section was analyzed under the slip deformation mechanism. The actual clamp manner of the specimen was modeled by setting correlative boundary condition, and the small angle deflection between tension loading axis and crystallography axis [100] was taken into account. The finite deformation numerical analysis of three-dimensional necking deformation for the specimen was performed by applying crystal plasticity theory associated with a numerical algorithm suggested by the first author. According to the comparison with experimental observation, the fact was confirmed that the numerical results could describe the loading elongation curve of the copper single crystal specimen under large strain tension reasonably, and the method could be used to investigate the necking characteristic in neck shape and the effect due to the small angle deflection. Further, the investigation into the influence of specimen cross-section shape on necking was also performed; the results on mechanical response and neck profile evolution obtained through modeling of cylindrical specimen were compared with those obtained with square cross-section specimen.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Hill R, Rice J R. Constitutive analysis of elastic-plastic crystal at arbitrary strain. J Mech Phys Solids, 1972, 20: 401–13

    Article  MATH  Google Scholar 

  2. Asaro R J, Rice J R. Strain localization in ductile single crystals. J Mech Phys Solids, 1977, 25: 309–338

    Article  MATH  Google Scholar 

  3. Peirce D, Asaro R J, Needleman A. Material rate dependence and localized deformation in crystalline solids. Acta Metall, 1983, 31: 1951–1976

    Article  Google Scholar 

  4. Kalidindi S R, Bronkhorst C A, Anand L. Crystallographic texture evolution in bulk deformation processing of FCC metals. J Mech Phys Solids, 1992, 40: 537–569

    Article  Google Scholar 

  5. Maniatty A M, Dawson P R, Lee Y S. A time integration algorithm for elasto-viscoplastic cubic crystals applied to modeling polycrystalline deformation. Inter J Num Meth Engrg, 1992, 35: 1565–1588

    Article  MATH  Google Scholar 

  6. Sarma G, Zacharia G. Integration algorithm for modeling the elastoviscoplastic response of polycrystalline materials. J Mech Phys Solids, 1999, 47: 1219–1238

    Article  MATH  Google Scholar 

  7. Asaro R J, Needleman A. Texture development and strain hardening in rate dependent polycrystals. Acta Metall, 1985, 33: 923–953

    Article  Google Scholar 

  8. Needleman A, Asaro R J, Lemonds J, et al. Finite element analysis of crystalline solids. Comp Methods Appl Mech Eng, 1985, 52: 689–708

    Article  MATH  Google Scholar 

  9. Watanabe O, Zbib H M, Takenouchi E. Crystal plasticity: micro-shear banding in polycrystals using Voronoi tessellation. Int J Plas, 1998, 14: 771–788

    Article  MATH  Google Scholar 

  10. Kuroda M, Tvergaard V. Shear band development predicted by a non-normality theory of plasticity and comparison to crystal plasticity predictions. Int J Solids Struct, 2001, 38: 8945–8960

    Article  MATH  Google Scholar 

  11. Hutchinson J W. Elastic-plastic behavior of polycrystalline metals and composites. Phil Proc R Soc London, 1970, A318: 247–272

    Google Scholar 

  12. Zhang K S. Microscopic heterogeneity and macroscopic mechanical behavior of a polycrystalline material. Acta Sin Mech (in Chinese), 2004, 36: 714–723

    Google Scholar 

  13. Hutchinson J W. Bounds and self-consistent estimates for creep of polycrystalline materials. Proc Roy Soc Lond, 1976, 348A: 101–127

    Google Scholar 

  14. Peirce D, Shih C F, Needleman A. A tangent modulus method for rate dependent solids. Comput Struct, 1984, 18: 875–887

    Article  MATH  Google Scholar 

  15. Zhang K S. A finite element algorithm for frystal viscoplastic finite deformation. Mech Sci Tech (in Chinese), 2001, 20(suppl.): 1–4

    Google Scholar 

  16. Xu Z M, Li L, Li J G, et al. Orientation and competitive growth of single crystal copper by continuous casing. J Synth Cryst (in Chinese), 1999, 28: 188–192

    Google Scholar 

  17. Hirth J P, Lothe J. Theory of Dislocations. 2nd ed. New York: John Wiley and Sons, 1982

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Civil and Architectural Engineering, Key Laboratory of Disaster Prevention and Structural Safety, Guangxi University, Nanning, 530004, China

    Zhang KeShi

  2. Department of Engineering Mechanics, Northwestern Polytechnical University, Xi’an, 710072, China

    Geng XiaoLiang

  3. State Key Laboratory of Solidification Processing, Northwestern Polytechnical University, Xi’an, 710072, China

    Li JinShan & Hu Rui

Authors
  1. Zhang KeShi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Geng XiaoLiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Li JinShan
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hu Rui
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhang KeShi.

Additional information

Supported by the National Natural Science Foundation of China (Grant Nos. 10472092 and 10662001) and the Aviation Science Foundation of China (Grant No. 04C53027)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zhang, K., Geng, X., Li, J. et al. On the tension necking of copper single crystal specimen under slip deformation mechanism. SCI CHINA SER E 50, 308–318 (2007). https://doi.org/10.1007/s11431-007-0038-9

Download citation

  • Received:

  • Accepted:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11431-007-0038-9

Keywords

Search

Navigation