On self-affine tiles that are homeomorphic to a ball

Abstract

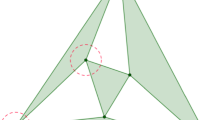
Let M be a 3 × 3 integer matrix which is expanding in the sense that each of its eigenvalues is greater than 1 in modulus and let ${\cal D} \subset {\mathbb{Z}^3}$ be a digit set containing |det M| elements. Then the unique nonempty compact set $T = T(M,{\cal D})$ defined by the set equation $MT = T + {\cal D}$ is called an integral self-affine tile if its interior is nonempty. If ${\cal D}$ is of the form ${\cal D} = \{ 0,v, \ldots ,(|\det M| - 1)v\} 0$, we say that T has a collinear digit set. The present paper is devoted to the topology of integral self-affine tiles with collinear digit sets. In particular, we prove that a large class of these tiles is homeomorphic to a closed 3-dimensional ball. Moreover, we show that in this case, T carries a natural CW complex structure that is defined in terms of the intersections of T with its neighbors in the lattice tiling {T + z: z ∈ ℤ³} induced by T. This CW complex structure is isomorphic to the CW complex defined by the truncated octahedron.