Abstract
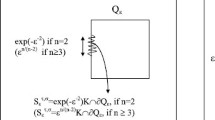
For equations of order two with the Dirichlet boundary condition, as the Laplace problem, the Stokes and the Navier-Stokes systems, perforated domains were only studied when the distance between the holes dε is equal to or much larger than the size of the holes ε. Such a diluted porous medium is interesting because it contains some cases where we have a non-negligible effect on the solution when (ε, dε) → (0, 0). Smaller distances were avoided for mathematical reasons and for these large distances, the geometry of the holes does not affect or rarely affect the asymptotic result. Very recently, it was shown for the 2D-Euler equations that a porous medium is non-negligible only for inter-holes distances much smaller than the size of the holes. For this result, the boundary regularity of holes plays a crucial role, and the permeability criterion depends on the geometry of the lateral boundary. In this paper, we relax slightly the regularity condition, allowing a corner, and we note that a line of irregular obstacles cannot slow down a perfect fluid in any regime such that ε ln dε → 0.
Similar content being viewed by others
References
Ahlfors L V. Lectures on Quasiconformal Mappings. Van Nostrand Mathematical Studies, 10. Toronto-New York-London: Van Nostrand, 1966
Allaire G. Homogenization of the Navier-Stokes equations in open sets perforated with tiny holes, I: Abstract framework, a volume distribution of holes. Arch Ration Mech Anal, 1990, 113: 209–259
Allaire G. Homogenization of the Navier-Stokes equations in open sets perforated with tiny holes, II: Noncritical sizes of the holes for a volume distribution and a surface distribution of holes. Arch Ration Mech Anal, 1990, 113: 261–298
Arsénio D, Dormy E, Lacave C. The vortex method for 2D ideal flows in exterior domains. ArXiv:1707.01458, 2017
Bonnaillie-Noël V, Lacave C, Masmoudi N. Permeability through a perforated domain for the incompressible 2D Euler equations. Ann Inst H Poincaré Anal Non Linéaire, 2015, 32: 159–182
Borsuk M, Kondratiev V. Elliptic Boundary Value Problems of Second Order in Piecewise Smooth Domains. North-Holland Mathematical Library, vol. 69. Amsterdam: Elsevier, 2006
DiPerna R J, Lions P-L. Ordinary differential equations, transport theory and Sobolev spaces. Invent Math, 1989, 98: 511–547
Gérard-Varet D, Lacave C. The two dimensional Euler equations on singular exterior domains. Arch Ration Mech Anal, 2015, 218: 1609–1631
Grisvard P. Elliptic Problems in Nonsmooth Domains. Monographs and Studies in Mathematics, vol. 24. Boston: Pitman, 1985
Gustafsson B, Vasil’ev A. Conformal and Potential Analysis in Hele-Shaw Cells. Advances in Mathematical Fluid Mechanics. Basel: Birkhäuser, 2006
Iftimie D, Lopes Filho M C, Nussenzveig Lopes H J. Two dimensional incompressible ideal flow around a small obstacle. Comm Partial Differential Equations, 2003, 28: 349–379
Jerison D, Kenig C E. The inhomogeneous Dirichlet problem in Lipschitz domains. J Funct Anal, 1995, 130: 161–219
Kozlov V A, Maz’ya V G, Rossmann J. Spectral Problems Associated with Corner Singularities of Solutions to Elliptic Equations. Mathematical Surveys and Monographs, vol. 85. Providence: Amer Math Soc, 2001
Lacave C. Uniqueness for two-dimensional incompressible ideal flow on singular domains. SIAM J Math Anal, 2015, 47: 1615–1664
Lacave C, Masmoudi N. Impermeability through a perforated domain for incompressible two dimensional Euler equations. Arch Ration Mech Anal, 2016, 221: 1117–1160
Lacave C, Miot E, Wang C. Uniqueness for the two-dimensional Euler equations on domains with corners. Indiana Univ Math J, 2014, 63: 1725–1756
Lacave C, Zlatos A. The Euler equations in planar domains with corners. Arch Ration Mech Anal, 2019, in press
Lions P-L. Mathematical Topics in Fluid Mechanics, Volume 1. Lecture Series in Mathematics and Its Applications, vol. 3. New York: Oxford University Press, 1996
Lions P-L, Masmoudi N. Homogenization of the Euler system in a 2D porous medium. J Math Pures Appl (9), 2005, 84: 1–20
Marchioro C, Pulvirenti M. Mathematical Theory of Incompressible Nonviscous Fluids. Applied Mathematical Sciences, vol. 96. New York: Springer-Verlag, 1994
Mikelic A. Homogenization of nonstationary Navier-Stokes equations in a domain with a grained boundary. Ann Mat Pura Appl (4), 1991, 158: 167–179
Mikelic A, Paoli L. Homogenization of the inviscid incompressible fluid flow through a 2D porous medium. Proc Amer Math Soc, 1999, 127: 2019–2028
Pommerenke C. Boundary Behaviour of Conformal Maps. Grundlehren der Mathematischen Wissenschaften, vol. 299. Berlin: Springer-Verlag, 1992
Sánchez-Palencia E. Boundary value problems in domains containing perforated walls. In: Nonlinear Partial Differential Equations and Their Applications. Collège de France Seminar, vol. III. Research Notes in Mathematics, vol. 70. Boston: Pitman, 1982, 309–325
Tartar L. Incompressible fluid flow in a porous medium: Convergence of the homogenization process. In: Nonhomogeneous Media and Vibration Theory. Berlin: Springer, 1980, 368–377
Acknowledgements
The first author was supported by the CNRS (program Tellus), the Agence Nationale de la Recherche: Project IFSMACS (Grant No. ANR-15-CE40-0010) and Project SINGFLOWS (Grant No. ANR-18-CE40-0027-01). The second author was supported by National Natural Science Foundation of China (Grant No. 11701016). This work has been supported by the Sino-French Research Program in Mathematics (SFRPM), which made several visits between the authors possible. The first author would like to acknowledge the hospitality and financial support of Peking University to conduct part of this work.
Author information
Authors and Affiliations
Corresponding author
Additional information
Dedicated to Professor Jean-Yves Chemin on the Occasion of His 60th Birthday
Rights and permissions
About this article
Cite this article
Lacave, C., Wang, C. A note on the regularity of the holes for permeability property through a perforated domain for the 2D Euler equations. Sci. China Math. 62, 1121–1142 (2019). https://doi.org/10.1007/s11425-018-9529-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11425-018-9529-8
Keywords
- ideal fluids
- homogenization in perforated domains
- shrinking obstacles and the porous medium
- domains with corners