Skip to main content
SpringerLink
Log in

Positive solutions for a Lotka-Volterra prey-predator model with cross-diffusion and Holling type-II functional response

  • Articles
  • Published:
Science China Mathematics Aims and scope Submit manuscript

Abstract

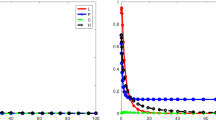
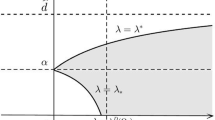
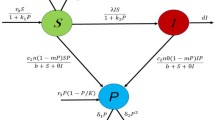
We consider a Lotka-Volterra prey-predator model with cross-diffusion and Holling type-II functional response. The main concern is the existence of positive solutions under the combined effect of cross-diffusion and Holling type-II functional response. Here, a positive solution corresponds to a coexistence state of the model. Firstly, we study the sufficient conditions to ensure the existence of positive solutions by using degree theory and analyze the coexistence region in parameter plane. In addition, we present the uniqueness of positive solutions in one dimension case. Secondly, we study the stability of the trivial and semi-trivial solutions by analyzing the principal eigenvalue of the corresponding linearized system, and then we characterize the stable/unstable regions of semi-trivial solutions in parameter plane.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Amann H. Fixed point equations and nonlinear eigenvalue problems in ordered Banach spaces. SIAM Rev, 1976, 18: 620–709

    Article  MATH  MathSciNet  Google Scholar 

  2. Casal A, Eilbeck J C, López-Gómez J. Existence and uniqueness of coexistence states for a predator-prey model with diffusion. Differential Integral Equations, 1994, 7: 411–439

    MATH  MathSciNet  Google Scholar 

  3. Dancer E N. On the indices of fixed points of mappings in cones and applications. J Math Anal Appl, 1983, 91: 131–151

    Article  MATH  MathSciNet  Google Scholar 

  4. Dancer E N. On positive solutions of some pairs of differential equations. Trans Amer Math Soc, 1984, 284: 729–743

    Article  MATH  MathSciNet  Google Scholar 

  5. Deuring P. An initial-boundary value problem for a certain density-dependent diffusion system. Math Z, 1987, 194: 375–396

    Article  MATH  MathSciNet  Google Scholar 

  6. Du Y H, Shi J P. Allee effect and bistability in a spatially heterogeneous predator-prey model. Trans Amer Math Soc, 2007, 359: 4557–4593

    Article  MATH  MathSciNet  Google Scholar 

  7. Dubey B, Das B, Hussain J. A predator-prey interaction model with self and cross-diffusion. Ecological Modelling, 2001, 141: 67–76

    Article  Google Scholar 

  8. Freedman H I. Deterministic Mathematical Models in Population Ecology. New York: Marcel Dekker Inc., 1980

    MATH  Google Scholar 

  9. Gui C, Lou Y. Uniqueness and nonuniqueness of coexistence states in the Lotka-Volterra competition model. Comm Pure Appl Math, 1994, 47: 1571–1594

    Article  MATH  MathSciNet  Google Scholar 

  10. Guo G, Wu J. Multiplicity and uniqueness of positive solutions for a predator-prey model with B-D functional response. Nonlinear Anal, 2010, 72: 1632–1646

    Article  MATH  MathSciNet  Google Scholar 

  11. Guo G, Wu J. The effect of mutual interference between predators on a predator-prey model with diffusion. J Math Anal Appl, 2012, 389: 179–194

    Article  MATH  MathSciNet  Google Scholar 

  12. Kan-on Y. Stability of singularly perturbed solutions to nonlinear diffusion systems arising in population dynamics. Hiroshima Math J, 1993, 23: 509–536

    MATH  MathSciNet  Google Scholar 

  13. Kindlmann P. Stability V S. complexity in model competition communities. In: Lecture Notes in Biomath, vol. 54. Berlin: Springer, 1984, 193–207

    Google Scholar 

  14. Ko W, Ryu K. Qualitative analysis of a predator-prey model with Holling type II functional response incorporating a prey refuge. J Differential Equations, 2006, 231: 534–550

    Article  MATH  MathSciNet  Google Scholar 

  15. Ko W, Ryu K. Coexistence states of a predator-prey system with non-monotonic functional response. Nonlinear Anal Real World Appl, 2007, 8: 769–786

    Article  MATH  MathSciNet  Google Scholar 

  16. Ko W, Ryu K. A qualitative study on general Gause-type predator-prey models with constant diffusion rates. J Math Anal Appl, 2008, 344: 217–230

    Article  MATH  MathSciNet  Google Scholar 

  17. Ko W, Ryu K. Analysis of diffusive two-competing-prey and one-predator systems with Beddington-Deangelis functional response. Nonlinear Anal, 2009, 71: 4185–4202.

    Article  MATH  MathSciNet  Google Scholar 

  18. Kuto K. Stability of steady-state solutions to a prey-predator system with cross-diffusion. J Differential Equations, 2004, 197: 293–314

    Article  MATH  MathSciNet  Google Scholar 

  19. Kuto K. Bifurcation branch of stationary solutions for a Lotka-Volterra cross-diffusion system in a spatially heterogeneous environment. Nonlinear Anal Real World Appl, 2009, 10: 943–965

    Article  MATH  MathSciNet  Google Scholar 

  20. Kuto K, Yamada Y. Multiple coexistence states for a prey-predator system with cross-diffusion. J Differential Equations, 2004, 197: 315–348

    Article  MATH  MathSciNet  Google Scholar 

  21. Kuto K, Yamada Y. Positive solutions for Lotka-Volterra competition systems with large cross-diffusion. Appl Anal, 2010, 89: 1037–1066

    Article  MATH  MathSciNet  Google Scholar 

  22. Leung A, Fan G. Existence of positive solutions for elliptic systems-degenerate and nondegenerate ecological models. J Math Anal Appl, 1990, 151: 512–531

    Article  MATH  MathSciNet  Google Scholar 

  23. Leung A W. Nonlinear Systems of Partial Differential Equations. Hackensack, NJ: World Scientific Publishing, 2009

    Book  MATH  Google Scholar 

  24. Li L. Coexistence theorems of steady states for predator-prey interacting systems. Trans Amer Math Soc, 1988, 305: 143–166

    Article  MATH  MathSciNet  Google Scholar 

  25. Lin Z, Pedersen M. Coexistence of a general elliptic system in population dynamics. Comput Math Appl, 2004, 48: 617–628

    Article  MATH  MathSciNet  Google Scholar 

  26. López-Gómez J. Positive periodic solutions of Lotka-Volterra reaction-diffusion systems. Differential Integral Equations, 1992, 5: 55–72

    MATH  MathSciNet  Google Scholar 

  27. Lou Y, Ni W M. Diffusion, self-diffusion and cross-diffusion. J Differential Equations, 1996, 131: 79–131

    Article  MATH  MathSciNet  Google Scholar 

  28. Lou Y, Ni W M. Diffusion vs cross-diffusion: an elliptic approach. J Differential Equations, 1999, 154: 157–190

    Article  MATH  MathSciNet  Google Scholar 

  29. Lou Y, Ni W M, Wu Y P. On the global existence of a cross-diffusion system. Discrete Contin Dyn Syst, 1998, 4: 193–203

    Article  MATH  MathSciNet  Google Scholar 

  30. Mimura M. Stationary pattern of some density-dependent diffusion system with competitive dynamics. Hiroshima Math J, 1981, 11: 621–635

    MATH  MathSciNet  Google Scholar 

  31. Mimura M, Kawasaki K. Spatial segregation in competitive interaction-diffusion equations. J Math Biol, 1980, 9: 49–64

    Article  MATH  MathSciNet  Google Scholar 

  32. Nakashima K, Yamada Y. Positive steady states for prey-predator models with cross-diffusion. Adv Differential Equations, 1996, 1: 1099–1122

    MATH  MathSciNet  Google Scholar 

  33. Nie H, Wu J H. Multiplicity and stability of a predator-prey model with non-monotonic conversion rate. Nonlinear Anal Real World Appl, 2009, 10: 154–171

    Article  MATH  MathSciNet  Google Scholar 

  34. Okubo A, Levin S A. Diffusion and Ecological Problems: Modern Perspectives, 2nd ed. New York: Springer-Verlag, 2001

    Book  Google Scholar 

  35. Pao C V. Strongly coupled elliptic systems and applications to Lotka-Volterra models with cross-diffusion. Nonlinear Anal, 2005, 60: 1197–1217

    Article  MATH  MathSciNet  Google Scholar 

  36. Ruan W H. Positive steady-state solutions of a competing reaction-diffusion system with large cross-diffusion coefficients. J Math Anal Appl, 1996, 197: 558–578

    Article  MATH  MathSciNet  Google Scholar 

  37. Ryu K, Ahn I. Positive coexistence of steady states for competitive interacting system with self-diffusion pressures. Bull Korean Math Soc, 2001, 38: 643–655

    MATH  MathSciNet  Google Scholar 

  38. Ryu K, Ahn I. Coexistence theorem of steady states for nonlinear self-cross diffusion systems with competitive dynamics. J Math Anal Appl, 2003, 283: 46–65

    Article  MATH  MathSciNet  Google Scholar 

  39. Ryu K, Ahn I. Positive steady-states for two interacting species models with linear self-cross diffusions. Discrete Contin Dyn Syst, 2003, 9: 1049–1061

    Article  MATH  MathSciNet  Google Scholar 

  40. Shigesada N, Kawasaki K, Teramoto E. Spatial segregation of interacting species. J Theoret Biol, 1979, 79: 83–99

    Article  MathSciNet  Google Scholar 

  41. Wang M, Wu Q. Positive solutions of a prey-predator model with predator saturation and competition. J Math Anal Appl, 2008, 345: 708–718

    Article  MATH  MathSciNet  Google Scholar 

  42. Yamada Y. Positive solutions for Lotka-Volterra systems with cross-diffusion. In: Handbook of differential equations: Stationary partial differential equations, vol. 6. Amsterdam: Elsevier/North-Holland, 2008, 411–501

    Google Scholar 

  43. Zhang C, Yan X. Positive solutions bifurcating from zero solution in a Lotka-Volterra competitive system with crossdiffusion effects. Appl Math J Chinese Univ Ser B, 2011, 26: 342–352

    Article  MATH  MathSciNet  Google Scholar 

  44. Zhang G, Wang W, Wang X. Coexistence states for a diffusive one-prey and two-predators model with B-D functional response. J Math Anal Appl, 2012, 387: 931–948

    Article  MATH  MathSciNet  Google Scholar 

  45. Zhou J, Mu C. Coexistence states of a Holling type-II predator-prey system. J Math Anal Appl, 2010, 369: 555–563

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Southwest University, Chongqing, 400715, China

    Jun Zhou

  2. Department of Mathematics, College of William and Mary, Williamsburg, VA, 23187-8795, USA

    Chan-Gyun Kim

Authors
  1. Jun Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chan-Gyun Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jun Zhou.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zhou, J., Kim, CG. Positive solutions for a Lotka-Volterra prey-predator model with cross-diffusion and Holling type-II functional response. Sci. China Math. 57, 991–1010 (2014). https://doi.org/10.1007/s11425-013-4711-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11425-013-4711-0

Keywords

MSC(2010)

Search

Navigation