On convergence of the inexact Rayleigh quotient iteration with the Lanczos method used for solving linear systems

Abstract

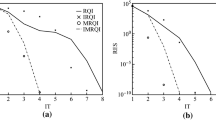
For the Hermitian inexact Rayleigh quotient iteration (RQI), we consider the local convergence of the inexact RQI with the Lanczos method for the linear systems involved. Some attractive properties are derived for the residual, whose norm is ξ _k , of the linear system obtained by the Lanczos method at outer iteration k+1. Based on them, we make a refined analysis and establish new local convergence results. It is proved that (i) the inexact RQI with Lanczos converges quadratically provided that ξ _k ⩽ ξ with a constant ξ ⩾ 1 and (ii) the method converges linearly provided that ξ _k is bounded by some multiple of $\tfrac{1} {{\left\| {r_k } \right\|}}$ with ‖r _k ‖ the residual norm of the approximate eigenpair at outer iteration k. The results are fundamentally different from the existing ones that always require ξ _k < 1, and they have implications on effective implementations of the method. Based on the new theory, we can design practical criteria to control ξ _k to achieve quadratic convergence and implement the method more effectively than ever before. Numerical experiments confirm our theory and demonstrate that the inexact RQI with Lanczos is competitive to the inexact RQI with MINRES.