Skip to main content
SpringerLink
Log in

Moving collocation methods for time fractional differential equations and simulation of blowup

  • Articles
  • Published:
Science China Mathematics Aims and scope Submit manuscript

Abstract

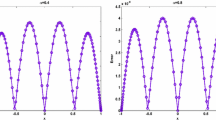
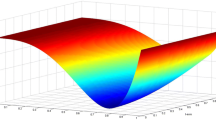
A moving collocation method is proposed and implemented to solve time fractional differential equations. The method is derived by writing the fractional differential equation into a form of time difference equation. The method is stable and has a third-order convergence in space and first-order convergence in time for either linear or nonlinear equations. In addition, the method is used to simulate the blowup in the nonlinear equations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bandle C, Brunner H. Blowup in diffusion equations: a survey. J Comput Appl Math, 1998, 97: 3–22

    Article  MathSciNet  MATH  Google Scholar 

  2. Budd C J, Carretero-González R, Russell R D. Precise computations of chemotactic collapse using moving mesh methods. J Comput Phys, 2005, 202: 463–487

    Article  MathSciNet  MATH  Google Scholar 

  3. Budd C J, Huang W, Russell R D. Moving mesh methods for problems with blow-up. SIAM J Sci Comput, 1996, 17: 305–327

    Article  MathSciNet  MATH  Google Scholar 

  4. Budd C J, Huang W, Russell R D. Adaptivity with moving grids. Acta Numer, 2009, 18: 111–241

    Article  MathSciNet  MATH  Google Scholar 

  5. Deng W. Numerical algorithm for the time fractional Fokker-Planck equation. J Comput Phys, 2007, 227: 1510–1522

    Article  MathSciNet  MATH  Google Scholar 

  6. Deng W. Finite element method for the space and time fractional Fokker-Planck equation. SIAM J Numer Anal, 2008, 47: 204–226

    Article  MathSciNet  Google Scholar 

  7. Huang W, Ma J, Russell R D. A study of moving mesh PDE methods for numerical simulation of blowup in reaction diffusion equations. J Comput Phys, 2008, 227: 6532–6552

    Article  MathSciNet  MATH  Google Scholar 

  8. Huang W, Ren Y, Russell R D. Moving mesh partial differential equations (MMPDEs) based upon the equidistribution principle. SIAM J Numer Anal, 1994, 31: 709–730

    Article  MathSciNet  MATH  Google Scholar 

  9. Huang W, Russell R D. A moving collocation method for the numerical solution of time dependent differential equations. Appl Numer Math, 1996, 20: 101–116

    Article  MathSciNet  MATH  Google Scholar 

  10. Jumarie G. A Fokker-Planck equation of fractional order with respect to time. J Math Phys, 1992, 33: 3536–3542

    Article  MathSciNet  MATH  Google Scholar 

  11. Li R, Tang T, Zhang P. Moving mesh methods in multiple dimensions based on harmonic maps. J Comput Phys, 2001, 170: 562–588

    Article  MathSciNet  MATH  Google Scholar 

  12. Lin Y, Xu C. Finite difference/spectral approximations for the time-fractional diffusion equation. J Comput Phys, 2007, 225: 1533–1552

    Article  MathSciNet  MATH  Google Scholar 

  13. Liu F, Yang C, Burrage K. Numerical method and analytical technique of the modified anomalous subdiffusion equation with a nonlinear source term. J Comput Appl Math, 2009, 231: 160–176

    Article  MathSciNet  MATH  Google Scholar 

  14. Ma J, Jiang Y, Xiang K. Numerical simulation of blowup in nonlocal reaction-diffusion equations using a moving mesh method. J Comput Appl Math, 2009, 230: 8–21

    Article  MathSciNet  MATH  Google Scholar 

  15. Mclean W, Thomée V. Numerical solutions via Laplace transforms of a fractional order evolution equations. J Integral Equations Appl, 2010, 22: 57–94

    Article  MathSciNet  MATH  Google Scholar 

  16. Mclean W, Thomée V. Maximum-norm error analysis of a numerical solution via Laplace transformation and quadrature of a fractional-order evolution equation. IMA J Numer Anal, 2010, 30: 208–230

    Article  MathSciNet  MATH  Google Scholar 

  17. Petzold L R. A descreption of DASSL: A differential/algebraic system solver. Sandia Labs Report SAND82-8637, Livermore, CA, 1982

  18. Podlubny I. Fractional Differential Equations. New York: Academic Press, 1999

    MATH  Google Scholar 

  19. Russell R D, Williams J F, Xu X. MOVCOL4: A moving mesh code for fourth-order time-dependent partial differential equations. SIAM J Sci Comput, 2007, 29: 197–220

    Article  MathSciNet  MATH  Google Scholar 

  20. Scherer R, Kalla S L, Boyadjev L, et al. Numerical treatment of fractional heat equations. Appl Numer Math, 2008, 58: 1212–1223

    Article  MathSciNet  MATH  Google Scholar 

  21. Schneider W R, Wyss W. Fractional diffusion and wave equations. J Math Phys, 1989, 30: 134–144

    Article  MathSciNet  MATH  Google Scholar 

  22. Soheili A R, Stockie J M. A moving mesh method with variable mesh relaxation time. Appl Numer Math, 2008, 58: 249–263

    Article  MathSciNet  MATH  Google Scholar 

  23. Tan Z, Zhang Z, Huang Y, et al. Moving mesh methods with locally varying time steps. J Comput Phys, 2004, 200: 347–367

    Article  MathSciNet  MATH  Google Scholar 

  24. Tang H, Tang T. Adaptive mesh methods for one and two-dimensional hyperbolic conservation laws. SIAM J Numer Anal, 2003, 41: 487–515

    Article  MathSciNet  MATH  Google Scholar 

  25. Tang T, Xu J. Adaptive Computations: Theory and Algorithms. Beijing: Science Press, 2007

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Economic Mathematics, Southwestern University of Finance and Economics, Chengdu, 611130, China

    JingTang Ma

  2. Department of Mathematics and Scientific Computing, Changsha University of Science and Technology, Changsha, 410076, China

    YingJun Jiang

Authors
  1. JingTang Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. YingJun Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to JingTang Ma.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ma, J., Jiang, Y. Moving collocation methods for time fractional differential equations and simulation of blowup. Sci. China Math. 54, 611–622 (2011). https://doi.org/10.1007/s11425-010-4133-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11425-010-4133-1

Keywords

MSC(2000)

Search

Navigation