Skip to main content
SpringerLink
Log in

On the convergence rate of a parallel nonoverlapping domain decomposition method

  • Published:
Science in China Series A: Mathematics Aims and scope Submit manuscript

Abstract

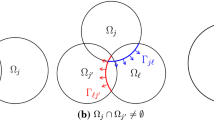
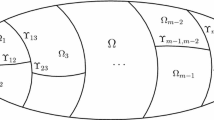
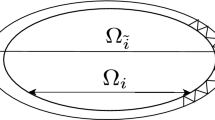
In recent years, a nonoverlapping domain decomposition iterative procedure, which is based on using Robin-type boundary conditions as information transmission conditions on the subdomain interfaces, has been developed and analyzed. It is known that the convergence rate of this method is 1 − O(h), where h is mesh size. In this paper, the convergence rate is improved to be 1 − O(h 1/2H−1/2) sometime by choosing suitable parameter, where H is the subdomain size. Counter examples are constructed to show that our convergence estimates are sharp, which means that the convergence rate cannot be better than 1 − O(h 1/2H−1/2) in a certain case no matter how parameter is chosen.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Chan T F, Mathew T P. Domain Decomposition algorithms. In: Acta Numerica 1994. Cambridge: Cambridge University Press, 1994, 61–143

    Google Scholar 

  2. Lions P L. On the Schwarz alternating method I. In: Glowinski R, Golub G H, Meurant G A, Periaux J, eds. Proceedings of the 1st International Symposium on Domain Decomposition Methods for Partial Differential Equations. Philadelphia: SIAM, 1988, 1–42

    Google Scholar 

  3. Smith B F, Bjorstad P E, Gropp W D. Domain Decomposition: Parallel Multilevel Algorithms for Elliptic Partial Differential Equations. Cambridge, Cambridge University Press, 1996

    MATH  Google Scholar 

  4. Toselli A, Widlund O. Domain Decompposition Methods—Algorithms and Theory. In: Computational Mathematics, Vol 34, New York: Springer, 2004

    Google Scholar 

  5. Lions P L. On the Schwarz alternating method III: A variant for nonoverlapping subdomains. In: Chan T F, Glowinski R, Perianx J, Widlund O B, eds. Third International Symposium on Domain Decomposition Methods for Partial Differential Equations. Philadephia: SIAM, 1990, 202–223

    Google Scholar 

  6. Bennethum S, Feng X. A domain decomposition method for solving a Helmholtz-like problem in elasticity based on the Wilson nonconforming element. M2AN Math Model Namer Anal, 31: 1–25 (1997)

    MATH  MathSciNet  Google Scholar 

  7. Despres B. Domain decomposition method and Helmholtz problem. In: Cohen G, Halpern L, Joly P, eds. Mathematical and Numerical Aspects of Wave Propagation Phenomena. Philadelphia: SIAM, 1991, 44–52

    Google Scholar 

  8. Feng X. Analysis of a domain decomposition method for the nearly elastic wave equations based on mixed finite element methods. IMA J Numer Anal, 18: 229–250 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  9. Deng Q. An analysis for a nonoverlapping domain decomposition iterative procedure. SIAM J Sci Comput, 18: 1517–1525 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  10. Deng Q. A nonoverlapping domain decomposition method for nonconforming finite element problems. Comm Pure Appl Anal, 2: 295–306 (2003)

    Google Scholar 

  11. Guo W, Hou L S. Generalization and accelerations of Lions’ nonoverlapping domain decomposition method dor linear elliptic PDE. SIAM J Numer Anal, 41: 2056–2080 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  12. Douglas J, Huang C S. Accelerated domain decomposition iterative procedures for mixed methods based on Robin transmission conditions. Calcolo, 35: 131–147 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  13. Douglas J, Huang C S. An accelerated domain decomposition procedures based on Robin transmission conditions. BIT, 37: 678–686 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  14. Qin L, Xu X. On a parallel Robin-type nonoverlapping domain decomoposition method. SIAM J Numer Anal, 44: 2539–2558 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  15. Ciarlet P G. The finite element method for elliptic problems. Amsterdam: North-Holland, 1978

    Book  MATH  Google Scholar 

  16. Sarkis M. Nonstandard coarse spaces and Schwarz methods for elliptic problems with discontinuous coefficients using non-conforming elements. Numer Math, 77: 383–406 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  17. Xu J. Iterative methods by space decomposition and subspace correction. SIAM Rev, 34: 581–613 (1992)

    Article  MATH  MathSciNet  Google Scholar 

  18. Xu J, Zou J. Some nonoverlapping domain decomposition methods. SIAM Rev, 40: 857–914 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  19. Xu J. Theory of Multilevel Methods. Ph.D. Thesis. Cornell University, Ithaca, NY, Rep AM-48, Pennsylvania State University, University Park, PA, August 1990

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Computational Mathematics and Scientific/Engineering Computing, Academy of Mathematics and Systems Science, Beijing, 100190, China

    Qin LiZhen, Shi ZhongCi & Xu XueJun

Authors
  1. Qin LiZhen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shi ZhongCi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xu XueJun
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xu XueJun.

Additional information

This work was supported by the National Basic Research Program of China (Grant No. 2005CB321701) and the National Natural Science Foundation of China (Grant No. 10731060)

Rights and permissions

Reprints and permissions

About this article

Cite this article

LiZhen, Q., ZhongCi, S. & XueJun, X. On the convergence rate of a parallel nonoverlapping domain decomposition method. Sci. China Ser. A-Math. 51, 1461–1478 (2008). https://doi.org/10.1007/s11425-008-0103-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11425-008-0103-2

Keywords

MSC(2000)

Search

Navigation