Abstract
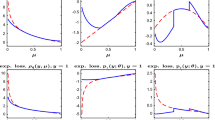
This paper discusses the asymptotic properties of the SCAD (smoothing clipped absolute deviation) penalized quasi-likelihood estimator for generalized linear models with adaptive designs, which extend the related results for independent observations to dependent observations. Under certain conditions, the authors proved that the SCAD penalized method correctly selects covariates with non-zero coefficients with probability converging to one, and the penalized quasi-likelihood estimators of non-zero coefficients have the same asymptotic distribution they would have if the zero coefficients were known in advance. That is, the SCAD estimator has consistency and oracle properties. At last, the results are illustrated by some simulations.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Nelder J A and Wedderburm R W M, Generalized models, Journal of the Royal Statistical Society: Series B, 1972, 135: 370–384.
Wedderburm R W M, Quasi-likelihood functions, generalized linear models, and the Gauss-Newton, Biometrika, 1974, 61: 439–447.
Chen K, Hu I, and Ying Z, Strong consistency of maximum quasi-likelihood estimators in generalized linear models with fixed and adaptive design, The Annals of Statistics, 1999, 27: 1155–1163.
Chen X and Chen X R, Adaptive quasi-likelihood estimate in generalized linear models, Science in China Seriers A Mathematics, 2005, 48(6): 829–846.
Yin C M and Zhao L C, Asymptotic normality and strong consistency of maximum quasi-likelihhod in generalized linear models, Science in China Series A Mathematics, 2006, 49: 145–157.
Gao Q B, Lin J G, Wu Y H, et al., Asymptotic normality of maximum quasi-likelihood estimators in generalized linear models with adaptive design, Statistics, 2012, 46(6): 833–846.
McCullagh P and Nelder J A, Generalized Linear Models, 2nd Ed. Chapman & Hall, New York, 1989.
Tibshirani R J, Regression shrinkage and selection via the LASSO, Journal of the Royal Statistical Society, Series. B, 1996, 58: 267–288.
Fan J and Li R, Variable selection via nonconcave penalized likelihood and its oracle properties, Journal of the American Statistical Association, Theory and Methods, 2001, 96(456): 1348–1360.
Wang L C, You Y, and Lian H, Convergence and sparsity of Lasso and group Lasso in high-dimensional generalized linear models, Statistical Papers, 2015, 56(3): 819–828.
Cui X H, Chen X, and Yan L, Quasi-likelihood Bridge estimators for high-dimensional generalized linear models, Communications in Statistics-Simulation and Computation, 2017, 46(10): 8190–8204.
Cui Y, Chen X, and Yan L, Adaptive Lasso for generalized linear models with a diverging number of parameters, Communications in Statistics — Theory and Methods, 2017, 46(23): 11826–11842.
Lai T L and Wei C Z, Least squares estimates in stochastic regression models with application to identification and control of dynamics systems, The Annals of Statistics, 1982, 10: 154–166.
Heuser H, Lehrbuch der Analysis, Teil 2. Teubner, Stuttgart, 1991.
Zou H and Li R, One-step sparse estimates in nonconcave penalized likelihood models, The Annals of Statistics, 2008, 36(44): 1509–1533.
Wang H, Li R, and Tsai C L, On the consistency of SCAD tuning parameter selector, Biometrika, 2007, 94: 553–568.
Author information
Authors and Affiliations
Corresponding authors
Additional information
This research was supported by the National Social Science Foundation of China under Grant No. 18BTJ040.
This paper was recommended for publication by Editor ZHU Liping.
Rights and permissions
About this article
Cite this article
Gao, Q., Zhu, C., Du, X. et al. The Asymptotic Properties of Scad Penalized Generalized Linear Models with Adaptive Designs. J Syst Sci Complex 34, 759–773 (2021). https://doi.org/10.1007/s11424-020-9134-8
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11424-020-9134-8