Abstract
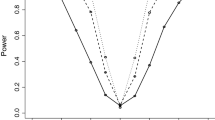
This paper develops a Wald statistic for testing the validity of multivariate inequality constraints in linear regression models with spherically symmetric disturbances, and derive the distributions of the test statistic under null and nonnull hypotheses. The power of the test is then discussed. Numerical evaluations are also carried out to examine the power performances of the test for the case in which errors follow a multivariate student-t (Mt) distribution.
Similar content being viewed by others
References
Wolak F, Testing inequality constraints in linear econometric models, Journal of Econometrics, 1989, 41: 205–235.
Wolak F, The local nature of hypothesis tests involving inequality constraints in nonlinear models, Econometrica, 1991, 59: 981–995.
Fahrmeir L and Klinger J, Estimating and testing generalized linear models under inequality restrictions, Statistical Papers, 1994, 35: 211–229.
Wan A T K and Ohtani K, Minimum mean squared error estimation in linear regression with an inequality constraint, Journal of Statistical Planning and Inference, 2000, 86: 157–173.
Andrews D W K, Testing when a parameter is on the boundary of the maintained hypothesis, Econometrica, 2001, 69: 683–734.
Geng W and Wan A T K, On the sampling performance of an inequality pre-test estimator of the regression error variance under LINEX loss, Statistical Papers, 2000, 41: 453–472.
Gill P, Murray W, and Wright M, Practical Optimization, Academic Press, New York, 1981.
Gourieroux C, Holly A, and Monfort A, Likelihood ratio test, wald test, and Kuhn-Tucker test in linear models with inequality constraints on the regression parameters, Econometrica, 1982, 50: 63–80.
Judge G, Yancey T, Bock M, and Bohrer R, The non-optimality of the inequality restricted estimator under squared error loss, Journal of Econometrics, 1984, 25: 165–177.
Ohtani K and Giles J, Testing linear restrictions on coefficients in a linear regression model with proxy variables and spherically symmetric disturbances, Journal of Econometrics, 1993, 57: 393–406.
Ohtani K and Wan A T K, On the sampling performance of an improved stein inequality restricted estimator, Australian and New Zealand Journal of Statistics, 1998, 40: 181–187.
Shapiro A, Asymptotic distribution of test statistics in the analysis of moment structures under inequality constraints, Biometrika, 1985, 72: 133–144.
Wan A T K, Risk comparison of the inequality constrained least squares and other related estimators under balanced loss, Economics Letters, 1994, 46: 203–210.
Wan A T K, Estimating the error variance after a pre-test for an inequality restriction on the coefficients, Journal of Statistical Planning and Inference, 1996, 52: 197–213.
Wan A T K, The exact density and distribution functions of the inequality constrained and pre-test estimators, Statistical Papers, 1997, 38: 329–341.
Yancey T, Judge G, and Bohrer R, Sampling performance of some joint one-sided preliminary test estimators under squared error loss, Econometrica, 1989, 57: 1221–1228.
Blattberg R and Gonedes N, Statistical Inference Under Order Restrictions, John Wiley, New York, 1974.
Fama E, The behaviour of stock market prices, Journal of Business, 1965, 38: 34–105.
Mandelbrot B, The variation of certain speculative prices, Journal of Business, 36: 394–419.
Sharpe W, Mean-absolute deviation characteristic lines for securities and portfolios, Management Sciences, 1971, 18: B1–B13.
Ullah A and Zinde-Walsh V, On the robustness of LM, LR, and W tests in regression models, Econometrica, 1984, 52: 1055–1066.
Ullah A and Phillips P, Distribution of the f-ratio, Econometric Theory, 1986, 2: 449–452.
Sutradhar B, Testing linear hypothesis with t error variable, Sankhya B, 1988, 50: 175–180.
Giles J, Pre-testing for linear retrictions in a regression model with spherically symmetric disturbances, Journal of Econometrics, 1991, 50: 377–398.
Qin H and Wan A T K, On the properties of the t- and f-ratios in linear regressions with non-normal errors, Econometric Theory, 2004, 20: 690–700.
Zaman A, Statistical Foundations for Econometric Techniques, Academic Press, New York, 1996.
Andrews D W K, Hypothesis testing with a restricted parameter space, Journal of Econometrics, 1998, 84: 155–199.
Barlow R E, Bartholomew D J, Bremner J N, and Brunk H D, A comparison of the stable and student distributions as statistical models for stock prices, Journal of Business, 1974, 47: 244–280.
Golderger A, One-sided and inequality tests for a pair of means, Workshop Series Paper 8629, Social Science Research Institute, University of Wisconsin-Madison, 1986.
Wolak F, An exact test for multiple inequality and equality constraints in the linear model, Journal of the American Statistical Association, 1987, 82: 782–793.
Lehmann E, Testing Statistical Hypothesis, John Wiley, New York, 1997.
Perlman M, One-sided problems in multivariate analysis, Annals of Mathematical Statistics, 1969, 40: 549–567.
Bohrer R and Chow W, Weights for one-sided multivariate inference, Applied Statistics, 1978, 27: 100–104.
Kudo A, A multivariate analogue of the one-sided test, Biometrika, 1963, 50: 403–418.
Siskind V, Approximate probability integrals and critical values for bartholomew’s test for ordered means, Biometrika, 1976, 63: 647–654.
Author information
Authors and Affiliations
Corresponding author
Additional information
Zhu’s research was supported by the National Natural Science Foundation of China under Grant No. 11301514 and National Bureau of Statistics of China under Grant No. 2012LZ012.
This paper was recommended for publication by Editor LIANG Hua.
Rights and permissions
About this article
Cite this article
Zhu, R., Zhou, S.Z.F. Testing inequality constraints in a linear regression model with spherically symmetric disturbances. J Syst Sci Complex 27, 1204–1212 (2014). https://doi.org/10.1007/s11424-014-1150-0
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11424-014-1150-0