Skip to main content
SpringerLink
Log in

Stability for the mix-delayed Cohen-Grossberg neural networks with nonlinear impulse

  • Published:
Journal of Systems Science and Complexity Aims and scope Submit manuscript

Abstract

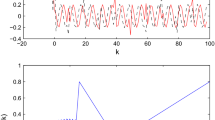
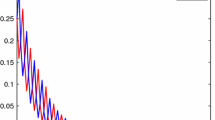
In this paper, the authors are concerned with the stability of the mix-delayed Cohen-Grossberg neural networks with nonlinear impulse by the nonsmooth analysis. Some novel sufficient conditions are obtained for the existence and the globally asymptotic stability of the unique equilibrium point, which include the well-known results on some impulsive systems and non-impulsive systems as its particular cases. The authores also analyze the globally exponential stability of the equilibrium point. Two examples are exploited to illustrate the feasibility and effectiveness of our results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. M. A. Cohen and S. Grossberg, Absolute stability and global pattern formation and parallel memory storage by competitive neural networks, IEEE Trans, Systems Man Cybernet, 1983, 13: 815–821.

    MATH  MathSciNet  Google Scholar 

  2. R. Zhang and J. Wu, A simple delayed neural network with large capacity for associative memory, Discrete and Continuous Dynamical Systems-Series B, 2004, (4): 851–863.

  3. Y. S. Huang, Resynchronization of delayed neural networks, Discrete and Continuous Dynamical Systems-Series A, 2001, (7): 397–401.

  4. J. D. Cao and J. Liang, Boundedness and stability for Cohen-Grossberg neural networks with time-varying delays, J. Math. Anal. Appl., 2004, 296: 665–685.

    Article  MATH  MathSciNet  Google Scholar 

  5. H. Ye, A. N. Michel, and K. Wang, Qualitative analysis of Cohen-Grossberg neural networks with multiple delays, Phys. Rev. E, 1995, 51: 2611–2618.

    Article  MathSciNet  Google Scholar 

  6. L. Wang and X. Zou, Exponential stability of Cohen-Grossberg neural networks, Neural Networks, 2002, (15): 415–422.

  7. L. Wang and X. Zou, Harmless delays in Cohen-Grossberg neural networks, Physica D, 2002, 170: 162–173.

    Article  MATH  MathSciNet  Google Scholar 

  8. W. J. Xiong and J. D. Cao, Global exponential stability of discrete-time Cohen-Grossberg neural networks, Neurocomputing, 2005, 64: 433–446.

    Article  Google Scholar 

  9. K. Yuan and J. D. Cao, An analysis of global asymptotic stability of delayed Cohen-Grossberg neural networks via nonsmooth analysis, IEEE Transactiona on Circuits and Systems, 2005, 345: 1854–1861.

    Article  MathSciNet  Google Scholar 

  10. H. J. Xiang and J. D. Cao, Exponential stability of periodic solution to Cohen-Grossberg-type BAM networks with time-varying delays, Neurocomputing, 2009, 72: 1702–1711.

    Article  Google Scholar 

  11. H. T. Lu, Global exponential stability analysis of Cohen-Grossberg neural networks, IEEE Transactions on Circuits and Systems II: Express Briefs, 2005, 52: 476–479.

    Article  Google Scholar 

  12. S. J. Guo and L. H. Huang, Stability analysis of Cohen-Grossberg neural networks, IEEE Transactions on Neural Networks, 2006, (17): 106–117.

  13. H. Akca, R. Alassar, and V. Corachav, Continuous-time additive Hopfield-type networks with impulses, J. Math. Anal. Appl., 2004, 290: 436–451.

    Article  MATH  MathSciNet  Google Scholar 

  14. P. Van Den Driessche and X. Zou, Global atractivity in delayed Hofield neural networks models, SIAM J. Appl. Math., 1998, 58: 1878–1890.

    Article  MATH  MathSciNet  Google Scholar 

  15. X. B. Liang, Global exponential stability and application of the Hopfield neural networks, Sci. China-Series A, 1995, 25: 523–532.

    Google Scholar 

  16. Y. H. Xia and P. J. Y. Wong, Global exponential stability of a class of retarded impulsive differential equations with applications, Chaos, Solitons, and Fractrals, 2009, 39: 440–453.

    Article  MathSciNet  Google Scholar 

  17. Z. Guan, G. Chen, and Y. Qin, On equilibria, stability and instability of Hopfield neural networks, IEEE Trans. Neural Networks, 2000, (2): 534–540.

  18. D. D. Bainov and P. S. Simeonov, Stability Theory of Differential Equations with Impulse Effects: Theory and Applications, Ellis Horwood, Chichester, 1989.

    Google Scholar 

  19. Z. C. Yang and D. Y. Xu, Impulsive effects on stability of Cohen-Grossberg neural networks with variable delays, Appl. Math. Comput., 2006, 177: 63–78.

    Article  MATH  MathSciNet  Google Scholar 

  20. S. Mohamad and K. Gopalsamy, Exponential stability preservation in semi-discretisations of BAM networks with nonlinear impulses, Commun Nonlinear Sci. Numer. Simul., 2009, (14): 27–50.

  21. Y. Zhao, Y. H. Xia, and W. Ding, Periodic oscillation for BAM neural networks with impulses, J. Appl. Math. Comput. 2008, 28: 405–423.

    Article  MATH  MathSciNet  Google Scholar 

  22. Z. K. Huang and Y. H. Xia, Global exponential stability of bam neural networks with transmission delays and nonlinear impulsive, Chaos, Solitons, and Fractals, 2008, 38: 489–498.

    Article  MATH  MathSciNet  Google Scholar 

  23. Z. Wen and J. T. Sun, Global asymptotic stability of delayed bam neural networks with impulses via nonsmooth analysis, Neurocomputing, 2008, 71: 1543–1549.

    Article  Google Scholar 

  24. Y. Zhang and J. T. Sun, Stability of impulsive neural networks with time delays, Phys. Lett. A, 2005, 348: 44–50.

    Article  Google Scholar 

  25. Z. Wang, Y. Liu, and X. Liu, On global asymptotic stability of neural networks with discrete and distributed delays, Phys. Lett. A, 2005, 345: 299–308.

    Article  MATH  Google Scholar 

  26. R. T. Rockafellar and R. J. B. Wets, Variational Analysis, Springer-Verlag, Berlin/Heideberg, 1998.

    Book  MATH  Google Scholar 

  27. F. H. Clarke, Optimization an Nonsmooth Analysis, Wiley, New York, 1983.

    Google Scholar 

  28. B. H. Pourciau, Hadamard theorem for Lacally Lipschitzian maps, J. Math. Anal. Appl., 1982, 85: 279–285.

    Article  MATH  MathSciNet  Google Scholar 

  29. A. Berman and R. J. Plemmons, Nonnegative Matrices in the Mathematical Science, Academic Press, New York, 1994.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Dynamics and Control, Beijing University of Aeronautics and Astronautics, Beijing, 100191, China

    Yong Zhao & Qishao Lu

  2. Department of Mathematics, University of Texas-Pan American, Edinburg, TX, 78539, USA

    Zhaosheng Feng

Authors
  1. Yong Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Qishao Lu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhaosheng Feng
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhaosheng Feng.

Additional information

This research is supported by the National Natural Science Foundation of China under Grant No. 10872014, the Natural Science Foundation of Fujian Province of China under Grant No. S0750008, and partially supported by UTPA Faculty Research Council under Grant No. 119100.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zhao, Y., Lu, Q. & Feng, Z. Stability for the mix-delayed Cohen-Grossberg neural networks with nonlinear impulse. J Syst Sci Complex 23, 665–680 (2010). https://doi.org/10.1007/s11424-010-0151-x

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11424-010-0151-x

Key words

Search

Navigation