Abstract
We introduce a simple financially constrained production framework in which heterogeneous firms and banks maintain multiple credit connections. The parameters of credit market interaction are estimated from real data in order to reproduce a set of empirical regularities of the Japanese credit market. We then pursue the metamodeling approach, i.e. we derive a reduced form for a set of simulated moments \(h(\theta ,s)\) through the following steps: (1) we run agent-based simulations using an efficient sampling design of the parameter space \(\Theta \); (2) we employ the simulated data to estimate and then compare a number of alternative statistical metamodels. Then, using the best fitting metamodels, we study through sensitivity analysis the effects on h of variations in the components of \(\theta \in \Theta \). Finally, we employ the same approach to calibrate our agent-based model (ABM) with Japanese data. Notwithstanding the fact that our simple model is rejected by the evidence, we show th at metamodels can provide a methodologically robust answer to the question “does the ABM replicate empirical data?”.









Similar content being viewed by others
Notes
For a review see Chen et al. (2012).
A network involving n firms and m banks connected by l links is said to be sparse when \(l \ll n \times m \), otherwise it is said to be dense. The Japanese credit market studied in Bargigli and Gallegati (2011), whose most recent data are employed in this paper, had \(l = 21,811\) connections over a maximum of \(n \times m = 2,674 \times 182 = 486,668\) in 2005.
By topological property we mean any observable which is defined on a binary network or on the binary representation of a weighted network. The latter is obtained from the binary representation of its weighted links, which is defined, for each couple of nodes (i, j), as \(a_{ij} = 1(w_{ij}>0)\), where
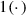 is the Indicator function and \(w_{ij}\) is the strength of the relationship between i and j.
is the Indicator function and \(w_{ij}\) is the strength of the relationship between i and j.Admittedly, with this choice we introduce potentially a small survivor bias in the model, since surviving firms are typically larger. However, the number of firm defaults is very limited over the parameter space we use for simulations and we choose the median (instead of the mean) in order to minimize the bias.
For more details see http://www.econophysics.jp/foc_kyoto/.
In detail, we employ random intercepts in a generalized linear mixed model estimated with the R Core Team (2015) package lme4.
The first 200 periods are discarded to get rid of transient dynamics that could introduce a bias in model statistics. Moreover, the long period of simulation does not represent a long-run analysis but a repeated business cycle analysis. In other words, we do not consider the presence of a trend in time-series by construction.
References
Alfarano S, Lux T, Wagner F (2005) Estimation of agent-based models: the case of an asymmetric herding model. Comput Econ 26(1):19–49
Barde S, van der Hoog S (2017) An empirical validation protocol for large-scale agent-based models, studies in economics 1712, school of economics. University of Kent, Canterbury
Bargigli L, Gallegati M (2011) Random digraphs with given expected degree sequences: a model for economic networks. J Econ Behav Organ 78(3):396–411
Bargigli L, Gallegati M, Riccetti L, Russo A (2014) Network analysis and calibration of the “leveraged network-based financial accelerator”. J Econ Behav Organ 99:109–125
Brenner T, Werker C (2007) A taxonomy of inference in simulation models. Comput Econ 30(3):227–244
Campolongo F, Saltelli A, Tarantola S (2000) Sensitivity analysis as an ingredient of modeling. Stat Sci 15(4):377–395
Canova F, Sala L (2009) Back to square one: identification issues in DSGE models. J Monet Econ 56:431–449
Chamberlain G (1980) Analysis of covariance with qualitative data. Rev Econ Stud 47(1):225–238
Chen S-H, Chang C-L, Du Y-R (2012) Agent-based economic models and econometrics. Knowl Eng Rev 27(6):187–219
Cioppa TM, Lucas TW (2007) Efficient nearly orthogonal and space-filling latin hypercubes. Technometrics 49(1):45–55
Dancik GM, Jones DE, Dorman KS (2010) Parameter estimation and sensitivity analysis in an agent-based model of leishmania major infection. J Theor Biol 262(3):398–412
Fagiolo G, Moneta A, Windrum P (2007) A critical guide to empirical validation of agent-based models in economics: methodologies, procedures, and open problems. Comput Econ 30(3):195–226
Gallegati M, Palestrini A, Delli Gatti D, Scalas E (2006) Aggregation of heterogeneous interacting agents: the variant representative agent framework. J Econ Interact Coord 1(1):5–19
Gouriéroux C, Monfort A (1996) Simulation-based econometric methods. CORE lectures. Oxford University Press, Oxford
Grazzini J, Richiardi M (2015) Estimation of ergodic agent-based models by simulated minimum distance. J Econ Dyn Control 51:148–165
Greenwald B, Stiglitz JE (1993) Financial market imperfections and business cycles. Q J Econ 108(77–114):1993
Kirman AP (1992) Whom or what does the representative individual represent? J Econ Perspect 6(2):117–136
Manzan S, Westerhoff F-H (2007) Heterogeneous expectations, exchange rate dynamics and predictability. J Econ Behav Organ 64(1):111–128
Nakagawa S, Schielzeth H (2013) A general and simple method for obtaining \(R^2\) from generalized linear mixed-effects models. Methods Ecol Evol 4(2):133–142
Park J, Newman MEJ (2004) Statistical mechanics of networks. Phys Rev E 2004(70):066117
R Core Team (2015) (2015) A language and environment for statistical computing. R (2015) Foundation for Statistical Computing, Vienna, Austria
Riccetti L, Russo A, Gallegati M (2013) Leveraged network-based financial accelerator. J Econ Dyn Control 37(8):1626–1640
Roustant O, Ginsbourger D, Deville Y (2012) DiceKriging, DiceOptim: two R packages for the analysis of computer experiments by kriging-based metamodeling and optimization. J Stat Softw 51(1):1–55
Salle I, Yildizoglu M (2014) Efficient sampling and meta-modeling for computational economic models. Comput Econ 44(4):507–536
Shin HS (2008) Risk and liquidity in a system context. J Financ Intermed 17(3):315–329
Stoker TM (1993) Empirical approaches to the problem of aggregation over individuals. J Econ Lit 31(4):1827–1874
Valente M (2005) Qualitative simulation modelling. Faculty of Economics, University of L’Aquila (Italy), Mimeo
Acknowledgements
We thank all the participants of the DISEI Department seminar of University of Florence held on November 17th 2015, the DISES Department seminar of Polytechnic University of Marche held on March 3rd 2016, the CEF2016 conference held on June 26–28 2016 in Bordeaux for their useful comments. A special thanks to Yoshi Fujiwara for providing the Japanese credit market data. All the usual disclaimers apply.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendices
Efficient sampling of \(\Theta \)
In order to simulate the ABM, we have to specify the value of its parameter vector \(\theta \). In general, some parameters can be set at a value which comes from the literature, experimental studies and empirical data. For other parameters, we can define an appropriate range of variation and study the behavior of the model within that range using Montecarlo simulations.
Random sampling from a uniform distribution, which is a common choice in Montecarlo exercises, is inefficient because it generates a high number of redundant sampling points (points very close to each other), while leaving some parts of the parameter space unexplored. A common alternative is importance sampling, which however requires prior information. A proper “design of experiment” (DOE) delivers instead a parsimonious sample which is nevertheless representative of the parameter space. In particular, representative samples are said to be “space filling”, since they cover as uniformly as possible the domain of variation.
The sampling scheme we adopt for the subspace of free parameters \(\theta = (r_{cb},\delta ,\mu )\), specified in Table 5, is the one suggested by Cioppa and Lucas (2007) and employed by Salle and Yildizoglu (2014). This scheme is based on Nearly Orthogonal Latin Hypercubes (NOLH). In the context of sampling theory, a square grid representing the location of sample points for a couple of parameters is a Latin square if there is only one sample point in each row and each column. A Latin hypercube is the generalization of this concept to an arbitrary number of dimensions, whereby each sample point is the only one in each axis-aligned hyperplane containing it. This property ensures that sample points are non collapsing, i.e. that the 1-dimensional projections of sample points along each axis are space filling. In fact, with this scheme, the sampled values of each parameter appear once and only once.
Basic Latin Hypercube schemes may display correlations between the columns of the \(k \times n\) design matrix X, where k is the number of parameters and n is the sample size for each parameter, especially when k is lower but close to n. Instead, an orthogonal design is convenient because it gives uncorrelated estimates of the coefficients in linear regression models and improves the performance of statistical estimation in general. In practice, in orthogonal sampling, the sample space is divided into equally probable subspaces. All sample points in the orthogonal LH scheme are then chosen simultaneously making sure that the total ensemble of sample points is a Latin Hypercube and that each subspace is sampled with the same density.
The NOLH scheme of Cioppa and Lucas (2007) improves the space filling properties of the resulting sample when \(k \lessapprox n\) at the cost of introducing a small maximal correlation of 0.03 between the columns of X. Furthermore, no assumptions regarding the homoskedasticity of errors or the shape of the response surface (like linearity) are required to obtain this scheme. The values of \(\theta = (r_{cb},\delta ,\mu )\) obtained from this scheme and used for simulations of Sect. 4 are reported in Table 7, while those employed for simulations of Sect. 5 are reported in Table 8.
Kriging regression
In the metamodeling selection exercise of Sect. 4, we estimate various Kriging models. These are generalized regression models, potentially allowing for heteroskedastic and correlated errors. The approach is widely used for ABM metamodeling in various fields (see e.g. Salle and Yildizoglu 2014; Dancik et al. 2010 and references therein). Using generalized regression is convenient since some of the parameters of our model are related to random distributions which naturally affect the variability of model output. The Kriging approach (Roustant et al. 2012) resorts to feasible generalized least squares by assuming a stationary correlation kernel \(K(h) = K(\theta _i-\theta _j)\), where \(\theta _i,\theta _j\) are distinct points in the parameter space \(\Theta \). K(h) takes the following general form:
where d is the dimension of \(\Theta \), and \(\lambda = (\lambda _1,\dots ,\lambda _d)\) is a vector of parameters to be determined. In particular, we employ for g the specifications of Table 9.
Since we work with noisy, potentially heteroskedastic observations, in our estimation the covariance matrix of residuals is determined as follows:
where R is the correlation matrix with elements \(R_{ij} = K(\theta _i-\theta _j)\) and \(\tau = (\tau _1^2,\dots ,\tau _n^2)\) is the vector containing the observed variance of model output at fixed points of the parameter space and n is the size of the NOLH design. ML estimation is performed on the “concentrated” multivariate Gaussian log-likelihood, obtained by substituting the vector of regression coefficients with their generalized least square estimator. The “concentrated” log-likelihood is a function of \(\sigma \) and \(\lambda \), which are the optimization variables of the estimation. The solution is obtained numerically through the quasi-Newton algorithm provided by the DiceKriging R Core Team (2015) package (Roustant et al. 2012).
Sensitivity analysis
Campolongo et al. (2000) define sensitivity analysis (SA) as the study of how uncertainty in the output of a model can be apportioned to different sources of uncertainty in the model input. In this respect, SA techniques should satisfy the two main requirements of being global and model free. By global, one means that SA must take into consideration the entire joint distribution of parameters. Global methods are opposed to local methods, which take into consideration the variation of one parameter at a time, e.g. by computing marginal effects of each parameter. By model independent, one means that no assumptions on the model functional relationship with its inputs, such as linearity, are required.
Campolongo et al. (2000) propose a global approach based on the decomposition of variance:
where h is a generic vector of moments. We see that \(V_i\) represents the variance of the main effect of parameter i, while all the other terms are related to interaction effects. From this general formula we can obtain the contribution of interaction effects \(S_{Ii}\) involving the parameter \(\theta _i\) as follows:
The multidimensional integral of the last line can be evaluated numerically using the extended FAST method described in Campolongo et al. (2000). The results of Fig. 5 show, for each parameter in \(\theta \), the main effect (C.2) and the interaction effect (C.1) on the components of \(h = (m,v,fb)\).
Rights and permissions
About this article
Cite this article
Bargigli, L., Riccetti, L., Russo, A. et al. Network calibration and metamodeling of a financial accelerator agent based model. J Econ Interact Coord 15, 413–440 (2020). https://doi.org/10.1007/s11403-018-0217-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11403-018-0217-8


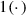 is the Indicator function and
is the Indicator function and