1 Introduction

Because of heavy rainfall and intensive snowmelts, both the streamflow and the amount of transported sediment increase in local rivers (Hejduk et al. 2006; Huang et al. 2007). Depending on the catchment, the discharged sediment loads may vary substantially between dry and wet periods and between different flood events. For example, Edwards and Owens (1991) based on the analysis of more than 4000 rainfall events over 28 years have found that the biggest five events from all recorded events accounted for 66% of the total erosion. According to USGS (2016), the sediment loads discharged from the catchment during one large flood event can account for more than half of the total load yielded throughout the whole year. Similar findings on the impact of extreme events on the sediment yield contribution in the catchment have been also reported, among others, by Larson et al. (1997) or Porto and Callegari (2019). The intensity of the sediment transported to lowland rivers depends however on the soil type and channel erosion (Trimble 1997; Banasik et al. 2012), and in urbanized areas on the build-up and wash-off processes taking place on impervious areas or roads (Di Modugno et al. 2015; Sikorska et al. 2015). Excessive sediment loads can have serious effects on water quality and water resources leading to silting of reservoirs, increased flood risk, damage to hydroelectric power plants or irrigation canals, a deterioration of water quality and higher treatment costs (Walling 2009). In this context, suspended sediment (SS, fine-grained material suspended in water) pose additional hazards because they absorb and carry associated pollutants such as pesticides (Bhadha et al. 2017), radionuclides (Porto et al. 2014), pharmaceuticals, household chemicals or heavy metals (Rossi et al. 2006; Schwarzenbach et al. 2006). Since SS can be transported down the river, these chemicals may threaten the health of people and the state of ecosystems far from their place of origin (Eyrolle et al. 2012; Sikorska et al. 2012; Schifman et al. 2018). Due to the increasing number of heavy rainfalls resulting from climate change, erosion processes are expected to be more intense in many regions of the world (Fiener et al. 2013; Pai et al. 2015), potentially increasing water and sediment-related hazards for people and ecosystems.

To control the quality and quantity of runoff discharged from small catchments, small low-volume reservoirs, also called detention or retention ponds, are often constructed on streams (Verstraeten and Poesen 2000; Krajewski et al. 2017b; Falco et al. 2020). In this work, the term small reservoir refers to a reservoir which volume amounts less than 0.5 million m3 and water-lifting height is up to 5 m, as proposed for polish conditions by Mioduszewski (2014). Note however that these thresholds may vary depending on local or national regulations. Originally, these reservoirs were only designed for flood reduction (Deletic 1998; Brydon et al. 2006). However, according to EPA (2002), such low volume reservoirs can trap 49–80% of SS entering the reservoir, and thus, they are capable of trapping the first stormflow, known to be the most contaminated (Färm 2002). This stormflow property is called a first flush effect (Deletic 1998). In these small reservoirs, the stormflow flowing into the reservoir is pre-treated by the sedimentation. Previous research indicates that the bed load can be fully trapped in such reservoirs (Banasik et al. 2012; Kondolf et al. 2014), whilst the finest grains are able to outflow from these reservoirs (Krajewski et al. 2017b). However, the trapping efficiency of bed load and fine sediments depends on the characteristics of the reservoir, its outlet structure and the transported material (Verstraeten and Poesen 2000). Capturing SS in the reservoir has the advantage that other accompanied pollutants absorbed in the sediment can also be captured in the reservoir (Stanley 1996). Thus, these small reservoirs have great potential for improving water quality locally at a small catchment scale. In addition, these on-stream reservoirs fit in well with the surrounding landscape providing recreational opportunities (Lawrence et al. 1996; Marsalek et al. 2002). In contrast to this, construction of larger reservoirs is usually linked to several negative impacts such as resettlement of residents, a substantial change of the landscape, and changes in hydromorphology and ecology downstream from the reservoir dam (Poeppl et al. 2015; van Oorschot et al. 2018). However, due to the deposition of SS together with accompanying pollutants, these small reservoirs can become toxic, particularly if they do not have any regular maintenance schedule or if the existing plan is based only on the pond age or its silting rate (Schifman et al. 2018). In this context, better understating of the sediment removal in such small reservoirs and an accurate estimate of the SS passage through these reservoirs is important for increasing our knowledge on the functioning of these small on-stream reservoirs.

Despite increasing interest in detention ponds for optimizing pond facilities (Ngo et al. 2016), flood protection (Sahoo and Pekkat 2018; Yazdi 2019), or optimizing water quality controls (Wang and Guo 2019), little is known about the functioning of these reservoirs. Basic measurements are missing as studies on sediment removal have traditionally been devoted to larger reservoirs (Morris and Fan 1998; Yang et al. 2014). Moreover, long-term records are not available due to the fast silting pace of these small on-stream reservoirs (Haregeweyn et al. 2012) which leads to complete siltation within just a few years of operation. Thus, more research devoted to the assessment of sediment removal in such small reservoirs is needed. In this context, there is a need for interdisciplinary research combining knowledge in the field of hydrology, sedimentology, water chemistry and quality, urban planning and engineering practice (Taylor and Owens 2009). An accurate estimate of SS captured in small reservoirs can assist in assessing the removal efficiency of already existing reservoirs and can help in designing more efficient new reservoirs or in maintenance works to optimize their functionality (Färm 2002; Krishnappan and Marsalek 2002). Optimizing reservoir maintenance works is important due to the high cost of sediment removal, which is often not considered in the pond design (Gregory 2014). For this purpose, simple approaches with a low demand on recorded data are needed.

With regard to the above, Verstraeten and Poesen (2001) and Krajewski et al. (2017a, 2019) have proven that the routing concept illustrates well the way a small reservoir operates. The clear advantage of the routing concept is that it is a simple and quick computational procedure with few input parameters, and in addition, it produces highly reliable results. Thus, this modelling concept appears to be an attractive alternative to more complex hydrodynamic models that are based on principles of mass and energy conservation for water and sediment (e.g. Kantoush et al. 2008; Hanmaiahgari et al. 2018), yet hydrodynamic models usually cannot be applied to small reservoirs due to a lack of recorded data. In our previous work (Krajewski et al. 2017a), a simple model based on the SS routing concept was proposed and tested with seven storm events on a small reservoir (1.3 ha and 14,500 m3) in Warsaw, Poland. This model adopts the concept of a continuously stirred tank reactor (CSTR) that was firstly introduced by Wilson and Barfield (1984). CSTR was further adapted by Verstraeten and Poesen (2001) and Wallis et al. (2006), who suggested that small reservoirs should be modelled as single chamber reservoirs. Despite good model performance, the major shortcoming of our previous work (Krajewski et al. 2017a) was the need to optimize the model parameter, the SS decay coefficient (κ), based on the water samples. This model parameter expresses the relative amount of sediments deposited in the reservoir in 1 s and, to keep the model as simple as possible, is assumed to be constant for one event. The SS decay coefficient may range from zero (no sediment deposition) to one (full sediment deposition). Thus, its estimation is crucial for accurately determining the outflow sediment graph. This property makes the model suitable for reconstructing SS concentrations (SSC) during past storm events, but its application for predicting new storms was very limited. In this current work, the authors further develop the concept of the SS routing through a small reservoir and attempt to overcome the abovementioned limitation by linking the SS decay coefficient to sediment particle properties in the pond inflow (i.e. the sediment settling velocity and water flow velocity). The properties of the particle size in the pond inflow have previously been proven to be important as they affect the overall removal efficiency of the pond (Greb and Bannerman 1997; Selbig et al. 2016).

In detail, the aims of this study are to:

  • propose an alternative method for identifying the suspended sediment decay coefficient (single parameter of the SS routing model) based on the particle properties (sediment settling velocity and water flowing velocity);

  • test its applicability for making simulations of SSC without the need to gather water samples for a model calibration;

  • compare estimates of the SSC in the outflow from a small detention pond derived with the newly proposed approach based on the particle properties with the estimates based on the model parameter optimization (based on recorded data);

  • assess the model’s predictive efficiency in simulating sediment graphs using the novel approach.

2 Material and study site

2.1 Detention pond and study area

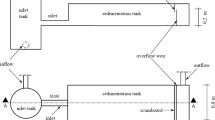
The detention pond studied in this work, Wyścigi Pond, is situated in the suburbs of Warsaw, Poland, on the Służew Creek (Fig. 1). The total length of the Służew Creek to its outlet to Wilanów Lake is 15.8 km. The contributing area to the Wyścigi Pond equals 28.7 km2 (Krajewski et al. 2017a), 25% of which is made up of impervious areas (Krajewski et al. 2020). The major source of sediment is wash-off from paved surfaces and unpaved open spaces (fields, wastelands, woodlands, parks, playgrounds, etc.) after heavy summer rainfalls, and thus, sediments are composed mostly of inorganic particles. With only few days of snow in the winter months, snow processes do not play any significant role in this catchment.

Fig. 1
figure 1

Locality map of the Służew Creek catchment and the Wyścigi Pond with inlet and outlet profiles marked. The flow direction of stormwater is marked with blue arrows on the reservoir scheme (right bottom)

Full size image

This on-stream pond was renovated in 2007 because of the entire loss of its capacity (Krajewski et al. 2017a) with the aim of cutting flood flows (Pietrak and Banasik 2009). In the period 2009–2015, due to further silting, the reservoir lost about 27% of its capacity (Krajewski et al. 2017b), even though its trap efficiency was estimated to be 71.1% in 2015 (Krajewski et al. 2017b). In 2015, at the normal pool level, the reservoir volume was 14,500 m3 and the surface area at the normal pool level equalled 1.27 ha. Its length equalled 240 m and the maximum width was 80 m (Krajewski et al. 2017b).

2.2 Field investigations

The field campaign carried out for the Wyścigi Pond included continuous measurement since 2009 of water stages and water temperature at the pond inlet and outlet. The continuous measurements were done with the use of level and temperature data loggers (Solinst Levelogger) in 30 min time intervals. Recorded levels were verified by comparing them with manual readings at the gauge staff. Discharges at the inlet and outlet were estimated according to water stage records and rating curves established for the inlet and outlet profiles (Krajewski et al. 2019). Suspended sediment transport at the inlet and outlet was established based on water samples (mixture of water and transported SS) taken manually from the stream in irregular intervals of 2 to 3 h during the passage of the stormflow and during the daytime. The sampler (volume of 1 l) was placed into stream until the container was filled with water and sediment (about 1–3 min). The concept behind this measurement is to keep the sampling velocity equal to the flow velocity and thus to avoid any fluctuation in the SS concentration caused by extending the time of sampling. The collected sediment samples were next brought to the laboratory for further analysis. The equipment used for taking SS samples did not allowed us to take any samples during the night time. This may have limitations in case of storm events occurring during the night time (Krajewski et al. 2018) and is discussed further in sect. 5. All measurements were carried out according to the standard methodology recommended by the Polish Institute of Meteorology and the Water Management National Research Institute (Barszczewska and Skąpski 2019). As a result, records from seven storm events collected in the summer months in the period 2015–2016 were available for this study.

In addition, as a verification of the abovedescribed streamflow samples, the density of SS was also determined for sediment samples dredged directly from the bottom of the Wyścigi Pond that were taken in May 2015 using the KC Kajak Sediment Core sampler (KC Denmark A/S 2020). In total, we took three core sediment samples from the middle part of the reservoir, each of the volume about 530 cm3. This core sediment sample can be seen as a benchmark sample for determining that the sediment estimates from streamflow samples are of the correct order of the magnitude.

2.3 Laboratory analysis

Based on water samples taken in the field, the grain size distribution, concentration and density of sediment particles were established in laboratory conditions.

Grain size distributions were determined based on water samples taken upstream of the reservoir during the passage of the storm events. For this purpose, the Mastersizer 2000 analyser (Malvern Instruments Ltd 2007) was used, which enables particles in the range 0.05 to 550 μm to be measured. The device works on the principle of the laser diffraction method (Low Angle Laser Light Scattering). Suspended particles cause laser light scattering. The scattering angle is inversely proportional to the grain size. Available software calculates and reports the results of this measurement. Obtained diameters are equal to diameters of spheres having the same volume as the particle (equivalent volume diameters). Hejduk et al. (2006) has proven that this method can be successfully applied to analyse sediment samples collected in small catchments.

Suspended sediment concentrations were established for water samples collected during the passage of flood flows taken upstream and downstream of the Wyścigi Pond by using gravitational analysis. Collected water samples were filtered through paper filters (⌀ = 125 mm, 84 g m−2) of a known weight and dried. The remaining dried solid component (together with the paper filter) was weighed, and the total mass of dried solids was determined. After subtraction of the mass of the paper filter from the total mass of the dried solids, the mass of the dried solids from the water sample was determined. Next, the SSC was calculated by dividing the mass of dried solids by the volume of the sample.

The SS density was measured for suspended sediments flowing into the reservoir in accordance with the pycnometric method (Blake and Hartge 1986), based on the weight of the device filled either with water or with water and sediment:

$$ {\rho}_s={\rho}_w\frac{m_1}{m_1+{m}_2-{m}_3} $$
(1)

where

ρs:

density of SS (g dm−3),

ρw:

density of water at temperature observed (g dm−3),

m1:

mass of suspended sediment (g),

m2:

mass of pycnometer filled with water (g),

m3:

mass of pycnometer filled with water and suspended sediment (g).

This method is very sensitive to any uncontrolled change in the mass and therefore gives the most reliable and reproducible results for samples with the mass of suspended matter exceeding 0.1 g (based on authors’ experience). In small, lowland catchments, particle concentrations even during flood flows do not always reach this threshold value (Hejduk et al. 2006; Krajewski et al. 2017b). Thus, samples with particle concentrations estimated to be lower than the threshold value should be excluded from the analysis to avoid a high estimation error.

As a result, the density of SS could be estimated for water samples taken upstream of the reservoir during two recorded flood events (of 18-11-2015 and 20-06-2016). In addition, the SS density was also computed for water samples collected directly after heavy rainfalls (in June–July 2016). As the sediment density, unlike the particle size, shows less variability in a cross section (Dąbkowski et al. 1982), it may be also reasonable to accept one average value based on all samples taken in the field.

3 Methods

3.1 Suspended sediment routing model

The process of suspended sediment (SS) routing through a small low-volume pond can be described using the concept of a single continuous stirred tank reactor, CSTR (Huber et al. 2006; Krajewski et al. 2017a):

$$ \frac{d\left(V{C}^{II}\right)}{dt}={I}_{(t)}{C}_{(t)}^I-{O}_{(t)}{C}_{(t)}^{II}-\kappa {V}_{(t)}{C}_{(t)}^{II} $$
(2)

where

d(VCII)/dt:

change in the SS mass in the reservoir (g s−1) at time t,

V(t):

reservoir volume (m3) at time t,

CI(t):

suspended sediment concentration in the reservoir inflow (g m−3),

CII(t):

suspended sediment concentration in the reservoir and in the reservoir outflow (g m−3),

I(t)CI(t):

suspended sediment mass entering reservoir (g s−1),

O(t)CII(t):

suspended sediment mass leaving reservoir (g s−1),

I(t):

inflow discharge (m3 s−1),

O(t):

outflow discharge (m3 s−1),

V(t)CII(t):

suspended sediment mass deposited in the reservoir (g s−1),

κ:

suspended sediment decay coefficient, model parameter (s−1).

The suspended sediment decay coefficient, κ in Eq. (2), is assumed to be a constant value for each event, despite the fact that the properties of particles inflowing to the reservoir and the amount of stored water vary over time during each event. This hypothesis on the constant model parameter results from the assumption that the model should be as simple as possible. Namely, it should have a low number of input data and be easy to apply, but at the same time, it should provide a reliable representation of the SS routing through a small reservoir with high efficiency of model simulations.

The model relying on Eq. (2) has been successfully tested and validated on small reservoirs, among others, by Wallis et al. (2006) and Krajewski et al. (2017a, 2019). This model is particularly applicable for predicting the pond effluent concentration and the trap efficiency during the passage of flood events. The advantages of the abovedescribed method are its simplicity, the small number of parameters (one parameter) and the high reliability of the obtained results. However, the major difficulty arises from the need to identify the model parameter i.e. the suspended sediment decay coefficient (κ) if water samples are not available.

3.2 Estimation of the suspended sediment decay coefficient from recorded data

The measured and modelled SSC at the outlet of the reservoir were compared for each event independently, and the model parameter was estimated using an optimization approach. This approach aims at searching values of the model parameter that minimize errors between the observed and simulated SSC via maximizing the efficiency criteria. In this study, we used the Nash-Sutcliffe efficiency (NSE) as a measure of the model performance. The basic concept of the optimization approach is illustrated in Fig. 2 for one example event. The horizontal axis represents the range of the model parameter values, whereas the Nash-Sutcliffe efficiency (NSE) of model simulations for this event is presented on the vertical axis. For this example event, if the model parameter equals to 5.1 × 10−5, the model efficiency approaches its maximum value, which is here 0.839. This pair of data (i.e. the optimal parameter value and the maximal NSE value) corresponds to one event and is referred to as an optimum in the further analysis. This procedure is repeated for each event independently, and thus, the corresponding model parameter is optimized for each event. These calculations were performed with the use of Solver Add-in of MS Excel. The Nash-Sutcliffe efficiency (Moriasi et al. 2007) can be calculated from:

$$ \mathrm{NSE}=1-\left[\frac{\sum_{i=1}^n{\left({X}_{i, obs}-{X}_{i, sim}\right)}^2}{\sum_{i=1}^n{\left({X}_{i, obs}-{\overline{X}}_{obs}\right)}^2}\right] $$
(3)
Fig. 2
figure 2

Identification of the SS decay coefficient (κ) by optimizing the Nash-Sutcliffe efficiency (NSE) for one example event no 6

Full size image

where

NSE:

Nash-Sutcliffe efficiency (−),

Xi,obs:

i-th observed value where i = 1, 2, …, n and n is the number of observed data points,

Xi,sim:

i-th simulated value,

\( {\overline{X}}_{\mathrm{obs}} \):

mean of observed data.

NSE can vary from – ∞ to 1.0. Values greater than zero indicate an acceptable model accuracy, whilst values higher than 0.5 indicate a good model performance (Knoben et al. 2019).

The presented optimization method can be used to identify the decay coefficient and to reconstruct the recorded sediment graph. However, this method is not applicable for predicting SSC during new events because the recorded sediment graph cannot be known, and thus, the parameter κ cannot be estimated before the event (optimized from the data). Therefore, Krajewski et al. (2017a) proposed a regression model that links the decay coefficient with the detention time (i.e. the time difference between centroids of the reservoir inflow and outflow hydrograph). Although such a solution enables predictions of sediment graphs to be made based on discharge information alone (only discharge data and not SSC data are required), the parameters of the regression model remain case-specific and need to be estimated for each study site from recorded discharge data. This property limits the application of the model to sites where at least recorded discharge data are available.

3.3 Conceptual approach to estimate the suspended sediment decay coefficient

Alternatively, the model parameter κ can be linked to the reservoir depth and particle properties as proposed by Chapra (2008):

$$ \kappa =\frac{v_s}{h} $$
(4)

where

υs:

particle settling velocity (m s−1),

h:

reservoir depth (m).

Note that Eq. (4) requires no additional calibration and both characteristics i.e. the reservoir depth and the particle settling velocity can be easily estimated. However, the abovementioned form seems to be suitable for static conditions (i.e. when particles settle vertically downwards). Thus, the trajectory and the velocity of particles flowing through the reservoir should be estimated in a different way. According to Camp (1946), the motion of a single particle under study flow conditions depends on the particle settling velocity, vs and the water flow velocity, vw (Fig. 3). Despite Camp’s theory identifies the most important factors that determine the particle trapping in the reservoir, it does not take into account other factors (turbulence, flocculation, group settling) that may also affect the sedimentation. Below we develop a suitable method for estimating the κ parameter by linking Chapra’s approach with Camp’s theory.

Fig. 3
figure 3

Suspended sediment settling in an ideal rectangular reservoir (after Camp 1946), h reservoir depth, L trajectory of a particle, Lr length of the reservoir, vw water flow velocity, vs settling velocity, vp particle flow velocity (resultant velocity)

Full size image

Thus, the particle flowing velocity through the reservoir, vp, resultant velocity, corresponding to settling velocity in Eq. (4), can be described as:

$$ {v}_p=\sqrt{v_s^2+{v}_w^2} $$
(5)

and the trajectory, Lp, corresponding to pond depth in Eq. (4) may be estimated from:

$$ {L}_p=\sqrt{{\overline{h}}^2+{L}_r^2} $$
(6)

where

\( \overline{h} \):

average reservoir depth for the storm event (m),

Lr:

length of the reservoir (m).

By dividing Eq. (5) through Eq. (6), one can easily calculate the model parameter κ:

$$ \kappa =\frac{v_p}{L_p}=\frac{\sqrt{v_s^2+{v}_w^2}}{\sqrt{{\overline{h}}^2+{L}_r^2}} $$
(7)

However, suitable estimation of the pond depth, the flow velocity as well as the settling velocity, is still needed.

3.4 Proposed methods for estimating model inputs

There are many methods available for calculating the particle settling velocity (υs) and Table 1 summarises three most commonly applied approaches suitable for this study. All these formulae rely on the particle diameter and the SS density, as well as on physical properties of the stormwater. Ideally, the sediment properties should be determined in laboratory conditions based on SS water samples collected in the field at the reservoir inlet. If such analysis is not possible, empirical formulae proposed in the literature can be used instead.

Table 1 Different formulas for estimating the particle settling velocity
Full size table

Following the assumption that the model parameter κ should be constant for the event, we suggest using the median diameter (d50) of SS in the inflow averaged for the event as an input for calculating the (average) particle settling velocity (υs). If more than one sediment sample is available, the average d50 can be calculated from the following formula:

$$ {\overline{d}}_{50}=\frac{\sum_{j=1}^n{d}_{50,j}\times {\varDelta Y}_j}{\sum_{j=1}^n{\varDelta Y}_j} $$
(8)

where

\( {\overline{d}}_{50} \):

average median diameter of SS inflowing to the reservoir during the storm event (μm),

d50,j :

median diameter of SS inflowing to the reservoir for j-th sample (μm) and j = 1, 2, …, l where l is the number of sediment samples per storm event,

ΔYj:

partial load of SS inflowing to the reservoir (kg) corresponding to the j-th sample.

Depending on the data availability, we suggest estimating the average density of SS in a similar way i.e. as an average over all samples.

Finally, the properties of the stormwater can be adopted according to physical tables for the assumed (known) temperature conditions. For temperate continental climate conditions according to the updated Köppen-Geiger climate classification (Peel et al. 2007), such as Central Europe where the studied pond is located, we recommend taking water properties adopted for a temperature of 15 °C. This value can be assumed as representative of stormwater in summer months in this region based on water temperature measures taken directly in the field.

Whilst small variations in water temperature (± 3 °C) have an indiscernible effect on the water properties, for reservoirs located in very different climatic conditions, particularly in tropical, arid, semi-arid or polar regions, other more suitable values should be tested.

The water flow velocity vw may be estimated based on records of inflow discharge and the cross-sectional area of the reservoir. Alternatively, vw can be computed by dividing the distance between inflow and outflow gauging stations through the detention time (the time difference between the centroids of the inflow and outflow hydrographs, average resilience time of stormwater in the reservoir):

$$ {v}_w=\frac{L_s}{T_d} $$
(9)

where

Ls:

distance between the reservoir inflow and outflow gauging station (m),

Td:

reservoir detention time (s).

Regarding the reservoir depth, we suggest taking the average reservoir depth for the event(s) determined based on the reservoir volume and area:

$$ \overline{h}=\frac{\sum {h}_{(t)}=\frac{V_{(t)}}{A_{(t)}}}{z} $$
(10)

where

\( \overline{h} \) :

average reservoir depth for the storm event (m)

h(t):

reservoir depth at time t (m),

V(t):

reservoir volume at time t (m3),

A(t):

reservoir surface area at time t (m2),

z:

number of time intervals of the storm event.

3.5 Evaluation criteria

The performance of the newly developed model and of the optimnited method was assessed based on two efficiency criteria i.e. the Nash-Sutcliffe efficiency (NSE), as described in sect. 3.2., and the Kling-Gupta efficiency (KGE). The latter consists of three components: correlation, coefficient of variation (variability error) and bias, and is computed as (Gupta et al. 2009):

$$ KGE=1-\sqrt{{\left(r-1\right)}^2+{\left(\frac{\sigma_{\mathrm{sim}}}{\sigma_{\mathrm{obs}}}-1\right)}^2+{\left(\frac{{\overline{X}}_{\mathrm{sim}}}{{\overline{X}}_{\mathrm{obs}}}-1\right)}^2} $$
(11)

where

KGE:

Kling-Gupta efficiency (−),

r:

Pearson coefficient (linear correlation between the simulation and observation),

σmod :

standard deviation of simulated data,

σobs:

standard deviation of observed data,

\( {\overline{X}}_{\mathrm{mod}} \):

mean of simulated data,

\( {\overline{X}}_{\mathrm{obs}} \):

mean of observed data.

The KGE is frequently used in recent years as a more balanced criteria for assessing the model performance that better accounts for the variable variability than the traditionally used NSE (Liu 2020). Similarly to NSE, KGE can take values from – ∞ to 1 but the interpretability of KGE values is slightly different than it is for NSE. According to Knoben et al. (2019), KGE values greater than − 0.41 indicate that a model improves upon the mean flow benchmark and values greater than 0.3 are consider as a good model performance, with the value of 1 standing for the best model fit. Use of an additional criterion (KGE) that is not used during the model calibration enables us to more objectively assess the model performance.

4 Results

4.1 Field investigations and laboratory analysis

In the period 2015–2016, seven storm events were recorded for the Wyścigi Pond. The characteristics of these events are summarized in Table 2. It can be seen that the maximum inflow and outflow of the reservoir reached very similar values for each of these events. This shows that the reservoir has a low flood storage capacity and thus a minimal impact on the flood peak reduction. By comparing the peaks in inflow and outflow of the reservoir, the peak reduction was estimated for the seven analysed events as being lower than 2.5%. This finding is in agreement with Krajewski et al. (2017b) who estimated this peak flow reduction to be slightly higher but still rather small (< 14%), and with previous research on this pond (Pietrak and Banasik 2009; Krajewski et al. 2017a).

Table 2 Characteristics of the recorded storm events
Full size table

In contrast to the discharge, the SSC decreased meaningfully after a stormflow passage throughout the pond for the analysed events, and thus, the outflow quality was clearly improved. For the seven analysed events, the reduction of SSC was estimated to be between 68.5 and 96.3%. This is slightly lower than the average reduction of SSC estimated in our previous work (83%) (Krajewski et al. 2017a) which was based on slightly different storm events (years 2014–2015). In the analysed period, there was no change in the field methodology, so the visible differences in the SSC can be attributed purely due to the differences between the storm events. These findings confirm that the Wyścigi Pond not only plays an important role in improving the quality of stormwater washed-off from the contributing area but also demonstrates that the SS reduction is decreasing with functioning time (comparing period 2014–2015 with 2015–2016).

The average diameter of SS grains (\( {\overline{d}}_{50} \)) in the inflow to the pond ranged from 27.4 to 51.8 μm. Average pond depths equalled 1.14 m and 1.34 m in a non-flood period and during analysed flood events, respectively. The estimated detention time for almost all events was less than 1 h. Figure 4 presents observed inflow and outflow for all seven flood events. Alternating increases and decreases in the discharge visible in the figure result from breaks in rainfalls (not shown). In the inflow to the reservoir (marked as light orange squares), one can clearly see the first flush effect for most of the events, which occurs when the peak of the pollutant concentration arises prior to the discharge peak (Deletic 1998). The first flush effect was observed for five out of seven recorded events. This first flush effect is typical of urbanized catchments and its occurrence demonstrates the opportunity to capture the first (most polluted) part of the washed-off stormwater in the on-stream detention pond, as is the case for the Wyścigi Pond. Hence, the proper functioning of this pond has an essential impact on improving water quality in Służew Creek and on the ecology of surrounding areas. It can be also seen from the figure that SSC are much lower in the outflow from the reservoir (dark orange points) in comparison to SSC measured at the reservoir inflow (light orange squares). This acknowledges that the reservoir is capturing the large amount of SSC entering the reservoir.

Fig. 4
figure 4

Inflow to and outflow from the Wyścigi Pond during seven recorded storm events

Full size image

The SS density estimates are presented in Table 3 for water samples taken upstream of the reservoir during two recorded flood events for which multiple samples were taken (of 18-11-2015 and 20-06-2016) and for additional single samples taken after heavy rainfalls (in June–July 2016, no further records on these storm events). The obtained dataset on water samples is characterized by a small variation in the SS density: the average value was 2.374 kg m−3 with a standard deviation of 118 kg m−3. The density of the sample taken directly from the reservoir bottom (10-05-2015) equals to 2440 kg m−3 and describes the density of sediment deposited in the middle part of the reservoir. This sample can be seen as a benchmark for the sediment samples taken directly from the streamflow. Therefore, it can be assumed that the estimated average SS density is representative of all inflow events recorded in the period 2015–2016.

Table 3 Suspended sediment density, ρs, of streamflow water samples entering the Wyścigi Pond
Full size table

4.2 Particle and flow velocities

Results of field and laboratory investigations (i.e. the average grain size \( {\overline{d}}_{50} \) for the event and the average density ρs) were used to estimate the settling velocities of sediment particles according to the methods presented in Table 1 for each individual storm event. Calculated velocities differ for individual events and vary between three applied methods (Table 4). The lowest particle settling velocities resulted from Zhang’s (after Wu 2007) formula (average = 0.84 × 10−3 m s−1), whilst the highest particle settling velocities were achieved according to Stokes (after Haan et al. 1994). The values computed according to the Goncarov (after Dąbkowski et al. 1982) method lie between those derived using the two previously mentioned methods, and range from 0.49 × 10−3 to 1.28 × 10−3 m s−1. The estimated water flow velocity is 100 times higher than the settling velocity (average = 111.9 × 10−3 m s−1), and it has a stronger effect on the particle movement and thus the particle resultant velocity. Hence, regardless of the method used for the settling velocity estimation, the resultant velocity remains the same.

Table 4 Settling velocities (vs) and particle flowing velocities (vp) of suspended sediments and water flow velocities (vw) for recorded storm events. Note that regardless of the method selected for the settling velocity estimation, the resultant particle flowing velocities have the same value as the water flow velocity
Full size table

4.3 Modelling approach

Next, the SS decay coefficient (κ), which is the only parameter of the sediment routing model, Eq. (2), was determined for each event independently using the two methods described in section 3.2. i.e. an optimization technique based on the Nash-Sutcliffe efficiency and the procedure developed in this work based on the sediment particle velocities (see section 3.3 to 3.4).

Regarding the first approach, Eq. (2) was rewritten in the finite difference form and solved for an effluent concentration. Model inputs were the inflow hydrograph and sediment graph, outflow hydrograph, reservoir volume and the decay coefficient. Next, observed and modelled SSCs at the outlet were compared, and the model efficiency was assessed according to the Nash-Sutcliffe efficiency (NSE, see Table 5). When using the optimized model parameter (SS decay coefficient, κ), NSE was greater than 0.5 (average = 0.697) for all analysed events. This indicates that the model can well reconstruct observed sediment graphs. However, this method is not suitable for predictions of future or unknown events because κ cannot be optimized in advance.

Table 5 Efficiency criteria, Nash-Sutcliffe efficiency (NSE) and Kling-Gupta efficiency (KGE), for modelled sediment graphs based on SS decay coefficient (κ) estimated according to the optimization method and a newly proposed method based on the particle flowing velocity and trajectory
Full size table

In contrast to the above method, the second approach proposed in this study is also suitable for sediment graph predictions as it links κ to the particle flowing velocity (υp), and thus, it enables the efficiency of SSC prediction to be evaluated. Figure 5 presents a comparison between the optimized and calculated decay coefficients. Surprisingly, all newly calculated parameters (regardless of the method used to estimate the particle settling velocity) were about 10 times higher than corresponding optimized parameters estimated directly from recorded SSC data. Consequently, all events produced negative NSE values. Hence, we introduced a correction (see Fig. 5) to accurately predict the effluent SSC. This gave positive NSE values for all events and these corrected values were very similar to those obtained through the optimization technique (where κ is optimized for each event), see Table 5. Also, values of KGE were similar for both methods i.e. based on the optimization technique and with the newly proposed method (after accounting for the correction factor) and for most events above the value of 0.3. This confirms a good model performance with the new method.

Fig. 5
figure 5

Relation between SS decay coefficients, optimized and calculated based on the particle flowing velocity and the trajectory, a dashed line indicates the necessary correction factor

Full size image

This finding demonstrates the potential of the conceptual routing model to predict effluent SSC based on the sediment particle properties and reservoir characteristics. Figure 6 shows computations based on the optimized parameter and on the newly developed formula for all seven events. Regardless of the calculation variant chosen, the estimated effluent SSCs were similar for both methods and the sediment graphs lie close to each other for all analysed events. This is also confirmed by the estimated NSE and KGE values (see Table 5 for both evaluation criteria).

Fig. 6
figure 6

Observed and modelled outflow from the Wyścigi Pond for seven recorded storm events

Full size image

5 Discussion

In this work, we proposed and tested a new method for deriving the sediment decay coefficient κ in the sediment routing model based on particle properties as an alternative to the optimization approach. First of all, our findings from the Wyścigi Pond demonstrate the difficulties in accurately predicting SSC in the outflow from a small on-stream reservoir and indicate a lack of knowledge regarding the functioning of such small reservoirs. However, our results demonstrate also that the newly proposed conceptual method, which uses the velocity formulae to estimate the SS decay coefficient, can be successfully employed to estimate the SSC in the outflow from the pond in place of the optimization technique. Several issues require a close discussion as described below.

In the newly proposed method, the computation of the κ parameter is based on the SS settling velocity (υs) and water flow velocity (υw). We have here tested three different formulae for the calculation of the SS settling velocity which all, despite differences, yielded relatively small values for υs in comparison to the water flow velocity (υw). Hence, the latter had a much larger impact on the calculation of the resultant particle flowing velocity (υp). Moreover, it is indisputable that the direct use of all the formulae for estimating the velocity gave poor model simulation results with negative values for NSE. Thus, the implementation of an additional correction factor was mandatory. Despite that, we do not reject the validity of any formula. Each of these methods was developed under different conditions and based on different assumptions. Factors such as grain shape, sediment source material used in the original experiment, concentration of sediment particles in water, or grain size (estimated according to specified method), can all affect the process of sedimentation in the pond. Thus, it is possible that ponds of different properties or sediments composed of different materials could be modelled better with one of these formulae. Thus, we recommend estimating the settling velocity according to one of the tested formulae and, if possible, verifying the outcomes by comparing them with field investigations and laboratory analysis on a set of storm events. The verification with field water samples is crucial in case the correction factor must be determined.

There is also a need of a further validation of the developed method with the use of new independent datasets i.e. either collected in different study sites or at the same study site but containing new storm events. Such dataset should enable a further verification and a further development of the proposed procedure.

Accounting for the correction factor yielded very good simulation results, as confirmed by Nash-Sutcliffe and Kling-Gupta efficiency, for all events and based on that, we recommend the use of the proposed routing method to model SSC in the outlet from other ponds with similar properties (climatic conditions and engineering characteristics) to the pond used in this study. However, we recommend to validate the correction factor first based on field data.

The need to introduce an additional constant, correction factor suggests that in the case of the analysed reservoir, the sedimentation process may be disturbed by other unknown factors. For instance, Haan et al. (1994) described four different types of settling that may occur in the reservoir: discrete (sediment particles fall independently of each other), flocculent (sediment particles coalesce and form larger aggregates), hindered (the fall velocity decreases due to a high sediment concentration) and compression (sediment particles form a stable structure, requiring compression for further settling). The occurrence of one or more of these factors may disturb the sedimentation in the pond. Hence, more research should be devoted to such small reservoirs to better explore the sedimentation process in such reservoirs.

Based on the above and our findings, the question arises as to which factors determine the efficiency of the suspended routing model. The routing sediment model used in this study has only one parameter, κ, which is estimated here based on the SS particle settling velocity and the water flow velocity. In our case, the water flow velocity played a dominant role in the SS particle sedimentation, and thus, detailed studies on its distribution in small on-stream reservoirs are needed. In particular, the importance of dead zones (where no routing takes place) should be analysed, as they may limit the sedimentation e.g. at reservoir banks. It is also important to identify factors that determine the validity of the SS particle settling velocity according to the developed formulae for simulating SSC in the pond of interest. To answer this question, more detailed research on the structure and shape of SS particles as well as on possible interactions between them in the analysed catchment, reservoir and possibly in other reservoirs, should be performed to better understand the process of particle settling in a small on-stream reservoir and its associated drivers.

The model estimates may be subject to uncertainties which were not accounted for in this study. These uncertainties may arrive from incomplete understanding of several factors such as the process of sediment build-up and wash-off, the pond functioning and its characteristics, the particle settling process, data quality and its representativeness of the cross-section and the structure of the routing model. Additionally, all other neglected processes that contribute to the SS in the outflow from the pond could contribute to this modelling uncertainty. However, due to a limited amount of data and number of water samples, it is not possible to quantify the dominant sources of this uncertainty. The uncertainty may also arise from the fact that the sediment samples were collected only during the day time. Collecting samples during the night time was not possible with the equipment used in this study. However, as seen by the analysis of recorded events, the variability in SSC during recorded events could be well captured. Thus, it is plausible to assume that the recorded events were well captured and the limitation due to the day time restriction of sampling may have rather caused that some other storm events occurred during the recorded period but were excluded from sampling because their peak happened during the night time. This however does not affect in anyway results from our study. Finally, the need to introduce an additional correction factor prior to using empirical formulae for deriving the model parameter is still not an optimal solution since the correction factor has to be estimated from recorded water samples, yet as long as the correction factor is based on a set of water samples, the formulae could be used for predicting SSC in the reservoir outlet without the need to gather additional SSC data. Hence, the conceptual approach based on the particle settling velocity has the potential to be used as a predictor of SSC instead of the optimization method originally proposed by Krajewski et al. (2017a). The method should, however, be used with caution if water samples are not available, as the need for introducing the correction factor cannot be verified.

6 Conclusions

In this work, a novel sediment routing modelling concept has been proposed to simulate the suspended sediment concentration (SSC) in the outlet from a small detention pond. The routing concept relies on the model introduced by Krajewski et al. (2017a), but it links the only model parameter, suspended sediment decay coefficient, to the particle settling velocity and the water flow velocity. In this way, the conceptual model does not require a direct calibration with storm events and can thus be applied for prediction purposes, which makes the approach very promising. To estimate the particle settling velocity, three different empirical formulae have been proposed that are based on sediment properties and the pond characteristics. The conceptual model was tested on a small detention pond in Warsaw with seven recorded storm events. Our findings demonstrate the applicability of the conceptual sediment routing model to simulate SSC in the outlet from a small on-stream reservoir. However, in the case of the analysed reservoir, the introduction of an additional constant correction was required to provide good simulation results. If this correction is established using a set of recorded water samples, it can be used to predict SSC during new storm events (i.e. without recorded data on SSC). The need to introduce the correction factor acknowledges the difficulties in accurately predicting SSC in the outflow from small on-stream reservoirs and indicates that there is still a lack of knowledge on the functioning of such small reservoirs.