The WULCA consensus characterization model for water scarcity footprints: assessing impacts of water consumption based on available water remaining (AWARE)

Abstract

Purpose

Life cycle assessment (LCA) has been used to assess freshwater-related impacts according to a new water footprint framework formalized in the ISO 14046 standard. To date, no consensus-based approach exists for applying this standard and results are not always comparable when different scarcity or stress indicators are used for characterization of impacts. This paper presents the outcome of a 2-year consensus building process by the Water Use in Life Cycle Assessment (WULCA), a working group of the UNEP-SETAC Life Cycle Initiative, on a water scarcity midpoint method for use in LCA and for water scarcity footprint assessments.

Methods

In the previous work, the question to be answered was identified and different expert workshops around the world led to three different proposals. After eliminating one proposal showing low relevance for the question to be answered, the remaining two were evaluated against four criteria: stakeholder acceptance, robustness with closed basins, main normative choice, and physical meaning.

Results and discussion

The recommended method, AWARE, is based on the quantification of the relative available water remaining per area once the demand of humans and aquatic ecosystems has been met, answering the question “What is the potential to deprive another user (human or ecosystem) when consuming water in this area?” The resulting characterization factor (CF) ranges between 0.1 and 100 and can be used to calculate water scarcity footprints as defined in the ISO standard.

Conclusions

After 8 years of development on water use impact assessment methods, and 2 years of consensus building, this method represents the state of the art of the current knowledge on how to assess potential impacts from water use in LCA, assessing both human and ecosystem users’ potential deprivation, at the midpoint level, and provides a consensus-based methodology for the calculation of a water scarcity footprint as per ISO 14046.

Introduction

For several decades, life cycle assessment (LCA) (ISO 14040 2006) has served as a decision-making tool to help reduce environmental impacts of products and services (Hellweg and Milà i Canals 2014). Recently, a new water footprint concept relying on a life cycle approach was framed in the ISO 14046 standard (ISO 14046 2014). In recent years, businesses have started to include water scarcity indicators (sometimes also called stress indicators) to assess potential impacts of water consumption. In the context of the ISO standard, this is the equivalent of a “water scarcity footprint” which addresses potential impacts associated with the quantity aspect of water use (i.e., water consumption) without considering the additional quality component of availability (e.g., water functionality as described in (Boulay et al. 2011a, b)). However, to date, no consensus-based approach exists to assess water scarcity impact as illustrated by the technical report (ISO 14073 2016) accompanying the ISO 14046 standard (ISO 14046 2014). It presents a series of water scarcity footprint examples which are simply not directly comparable, because the characterization models have different scales and ranges, and are based on different modeling choices, with some more human health or ecosystem quality oriented (Boulay et al. 2014). The need for a consensus-based method emerged from method developers and several environmental label and declaration initiatives wishing to use global metrics and ensure comparability (Galatola and Pant 2014; ISO 14046 2014; Boulay et al. 2015b) and was identified as priority by the UNEP-SETAC Life Cycle Initiative (Jolliet et al. 2014). The Water Use in LCA (WULCA) Working Group took over this task by bringing together method developers and experts in LCA, hydrology, and ecology from academia, public and private sectors.

In January 2014, building on the water use in LCA framework (Bayart et al. 2010; Kounina et al. 2013), WULCA commenced a 2-year activity aiming at developing consensus-based indicator(s) for water use impact assessment focusing first on a generic scarcity-based “proxy” midpoint indicator (labeled proxy as it does not lead directly to endpoint impacts on human health nor ecosystem quality specifically) applicable to water consumption (surface and groundwater). Unless specified, the terminology used in this paper is compliant with the ISO (14046 2014) standard, which can be consulted for detailed definitions. The term scarcity is retained here for compatibility with ISO 14046, although no difference with the term “stress” has been found in this context and other definitions of scarcity exist (Schyns et al. 2015). This paper presents the process that was established to answer the following introduced question and the resulting method. This method was approved and recommended as part of the UNEP-SETAC Life Cycle Initiative Flagship Project on impact assessment method recommendations (UNEP 2017) and applied on a series of illustrative case studies available online (www.wulca-waterlca.org).

Consensus process and member’s participation

This consensus work built on previous WULCA deliverable, specifically the quantitative method comparison which identified the different modeling choices made in existing scarcity indicators and their influence on the results (Boulay et al. 2015c). As the consensus building work started in 2013, participation was sought in four different ways: 1—Active members, 2—Volunteered experts, 3—Invited experts, and 4—Pellston workshop participants. The core working group (and authors of this paper) was composed of previous method developers on water use in LCA as well as additional members who demonstrated interest in this work and could contribute as “active members.” An open call for participation was made to the LCA community at SETAC meetings and via the Global Guidance UNEP-SETAC Life Cycle Initiative Flagship project recruitment, following the “Active members” time commitment description provided on the WULCA website. Members who indicated a desire to participate as “experts” were added to a mailing list, amounting to over 100 names, which were used for punctual consultations, including workshop invitation, dissemination, and experts surveys. In addition, for the expert workshops, specific expertise was invited on hydrological models and Environmental Water Requirements (EWR), including Aquaduct (Francis Gassert, (Gassert et al. 2013)), WaterGap (Petra Döll, (Alcamo et al. 2003)), LPJmL (Dieter Gerten, (Bondeau et al. 2007)), and H08 (Naoki Shirakawa, (Hanasaki 2010)). Lastly, the final consensus was approved in a Pellston workshop in January 2016, following the Pellston workshop representation rules as described in the UNEP-SETAC, Life Cycle Initiative report (2017) and applied on the required (10) number of case studies.

Method development

Identifying the right question

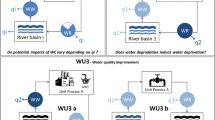
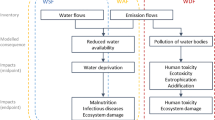
Water issues are complex and several relevant questions can be asked, such as understanding the potential to reduce water availability in a specific location, to increase competition among water users, or to adversely impact humans or ecosystems. Answering each question requires the development of a specific indicator. In LCA, indicators aim at quantifying potential environmental impacts of human interventions (such as water use or consumption) ultimately affecting three areas of protection: human health, ecosystem quality, and resource depletion (Jolliet et al. 2004). Preliminary discussions within this working group identified the relevant question from an LCA perspective regarding potential impacts of water consumption at the midpoint level to be “What is the potential to deprive another freshwater user (human or ecosystem) by consuming freshwater in this region?” (Boulay et al. 2015a). Note that potential deprivation from water degradation, as assessed in Boulay et al. (2011d) was not included in this indicator in order to avoid risks of double counting with water quality indicators when applied systematically.

From withdrawal-to-availability to demand-to-availability and beyond

When potential impacts from water use started to be integrated in LCA, indices based on the ratio of water withdrawal-to-availability (WTA) were used as characterization factors (Frischknecht et al. 2008; Pfister et al. 2009). Note that the term availability in this paper is used in the hydrological sense of precipitation minus evapotranspiration and hence does not include water quality aspects as specified in ISO 14046 (2014). While water withdrawal comprises the total water input into a product system, water consumption is defined as the fraction of water withdrawal which has become unavailable for the originating river basin users due to evapo(transpi)ration, product integration, or discharge into other basins and the sea. Hence, subsequently, methods based on water consumption-to-availability (CTA) ratio were developed, with the reasoning that water withdrawn from the environment and released in the same watershed (for cooling purposes for example) does not generally contribute to local water scarcity (Boulay et al. 2011c; Hoekstra et al. 2012; Berger et al. 2014) (even if local impacts may occur between the withdrawal and release points (Loubet et al. 2013)). Outcomes from expert discussions within WULCA (Boulay et al. 2015a) first identified the need to transition from WTA and CTA towards a demand-to-availability ratio (DTA), in order to better answer the overarching question identified above (Boulay et al. 2014) since both ecosystem water demand and human consumption are considered in “demand.” The proposal was accepted by a panel of 48 LCA experts from academia, industry, and governmental institutions (Boulay et al. 2015a) with, however, one main limitation identified, in addition to the challenge associated with quantifying ecosystem water demand. The DTA ratio (similarly to CTA and WTA) fails to represent the absolute water availability (per unit of surface). It only focuses on a metric relative to the use, resulting in loss of information. For example, a DTA ratio of 0.5 describes that half of the water is required by current users, but whether this amount of water is 10 or 1,000,000 m³ for the same area is unknown. This sometimes leads to arid areas showing less scarcity than known water-abundant regions (Berger and Finkbeiner 2013) and the relevance of this for LCA application can be questionable (Boulay et al. 2015a). Three proposals emerged during the workshops, as described in Boulay et al. (2015a) that could overcome this limitation, called DTA_A, DTAx, and 1/AMD. DTA_A is based on a demand-to-availability (DTA) ratio but includes a filter for arid regions. DTA_X is the product of two parameters: one representing the relative availability (DTA) and one representing absolute availability (AAv) per unit of surface (see supplementary material for complete description). The last one, 1/AMD, the inverse of availability minus demand, was retained through consensus following the criteria described below.

WULCA’s process for scarcity method selection

First, a pre-selection criterion was used to evaluate the relevance of each proposal with respect to the question to be answered, followed by four main criteria: 1. Stakeholder acceptability, 2. Robustness with closed basins, 3.Influence of normative choice, and 4. Physical meaning.

The pre-selection criterion of relevance led to the elimination of the first model DTA_A, which includes a filter for arid region using the maximal value (e.g., all regions with evapotranspiration higher than five times the local precipitation are set to the maximum value of the indicator). This choice showed a relatively high influence (17% of the world’s land surface, corresponding to 16% of the world’s water consumption) and actually corresponded to transforming the model into an aridity index for these areas, and the relevance of this choice in relation to the question to answer was judged too low based on the unanimous expert’s judgment of the co-authors. Hence, the DTA_A method was not further investigated.

Second, the four main criteria, which are further described in the SI, were used to guide the decision as shown in Table 1.

Table 1 Evaluation criteria and results for DTAx and 1/AMD

The result of the criteria analysis showed a preference towards a characterization factor based on 1/AMD: (1) stakeholder’s acceptability was higher for 1/AMD and included a larger diversity of stakeholders (consultants, industry, and government) and (2) 9 of the 13 closed or closing watersheds (identified as already showing signs of water scarcity related issues, see ESM) showed higher values (based on ranking and value percentile of maximum) in comparison to one for DTAx. Of the remaining three, the Orange watershed (not included in the table above) and two sub-watersheds of the Ganges and of the Indus showed higher ranking with DTAx but higher value percentile with 1/AMD. (3) The main normative choice of the 1/AMD method was judged as more acceptable to justify. One can understand intuitively that when demand is equal to or larger than availability (D ≥ A) (situation observed in 12% of the global area as per Tables S2 and S3 in SI), the potential to deprive other users is maximal as there is already deprivation occurring (i.e., users not having their water needs satisfied). Hence, the entire inventory of water consumed will cause deprivation. It is, however, more difficult to justify the normative choice in DTAx (which affects all values) and which arbitrarily sets absolute availability and relative availability to contribute equally to the potential of deprivation. Lastly, (4) the intrinsic meaning of both methods were discussed in the group. The meaning of DTAx is a combination of absolute and relative availability, with both parameters being equally correlated to the results on a global level, and the meaning of 1/AMD is the inverse of the remaining water available after demand has been met. The approach based on 1/AMD conserves a physical meaning with simple and clear units up for demand ≤ availability (on 87% of world surface), whereas DTAx units could not be identified meaningfully. Details on quantitative criteria assessment (1 and 2) are given in SI. Qualitative criteria were assessed through discussion among the co-authors and consensus, although not necessarily unanimity, was achieved when a large majority of the co-authors agreed, and dissenting points of view were noted and reported.

The recommended method is therefore based on 1/AMD; however, a minority of the co-authors would have preferred to recommend both methods due to the underlying conceptual differences between them. Although the group reached consensus on 1/AMD, it was also recommended to use a conceptually different method in parallel for sensitivity studies to test and improve the robustness of the conclusion.

Method description

Approach selected

The recommended method, based on 1/AMD, is based on the inverse of the difference between availability per area and demand per area instead of the ratio (Eq. (1) and Eq. (2)). It quantifies the potential of water deprivation, to either humans or ecosystems, and serves in calculating the impact score of water consumption at midpoint in LCA or to calculate a water scarcity footprint as per ISO 14046. It is based on the available water remaining (AWARE) per unit of surface in a given watershed relative to the world average, after human and aquatic ecosystem demands have been met. This method builds on the assumption that the potential to deprive another user of water (resulting from the multiplication of the inventory with the characterization factor, CF_AWARE, Eq. (5)) is directly proportional to the amount of water consumed (inventory) and inversely proportional to the available water remaining per unit of surface and time in a region (watershed) (cf. Eq. (5) and Fig. 1). Additional discussion and justification on this assumption can be found in the following publications: the first one justifying the use of the available water minus environmental demand in the denominator (Hoekstra 2016) and the answer to this paper explaining the reason for including the human demand as well (Pfister et al. 2017). When the value of the demand is equal to or larger than the availability (negative AMD), the characterization factor (CF) is set to be maximal since the equation would no longer be continuous nor hold the same meaning (Eq. (4a)). The CF is normalized (Eq. (3)) and cutoffs are applied (Eq. (4a) and Eq. (4b)). This is further described below.

$$ {\mathrm{AMD}}_i=\frac{\left(\mathrm{Availability}-\mathrm{HWC}-\mathrm{EWR}\ \right)}{\mathrm{Area}} $$

(1)

$$ {\mathrm{STe}}_i=\frac{1}{{\mathrm{AMD}}_i} $$

(2)

$$ {\mathrm{CF}}_{\mathrm{AWARE}}=\frac{{\mathrm{STe}}_i}{{\mathrm{STe}}_{\mathrm{world}\ \mathrm{avg}}}=\frac{\overline{{\mathrm{AMD}}_i}}{{\mathrm{AMD}}_i}=\frac{{\mathrm{AMD}}_{\mathrm{world}\ \mathrm{avg}}}{{\mathrm{AMD}}_i},\mathrm{for}\ \mathrm{Demand}< Availability $$

(3)

$$ {\mathrm{CF}}_{\mathrm{AWARE}}=\operatorname{Max}=100,\mathrm{for}\ \mathrm{Demand}\ge {\mathrm{Availability}\ \mathrm{or}\ \mathrm{AMD}}_{\mathrm{i}}<0.01\kern0.5em \times {\mathrm{AMD}}_{\mathrm{world}\ \mathrm{avg}} $$

(4a)

$$ {\mathrm{CF}}_{\mathrm{AWARE}}=\operatorname{Min}=0.1\kern0.5em \mathrm{for}\kern0.5em {\mathrm{AMD}}_{\mathrm{i}}>10\kern0.5em \times \kern0.5em {\mathrm{AMD}}_{\mathrm{world}\ \mathrm{avg}} $$

(4b)

Fig. 1

Relationship between deprivation potential and AMD in region i, as described by AWARE CFs

where demand refers to the sum of human water consumption (HWC) and environmental water requirements (EWR) and availability is the actual runoff (including human impacts on flow regulation), all calculated in m³/month and area in m². AMD _i is calculated in m³/m²·month and the remaining volume of water available for use once demand has been met, per unit area and time (m³/m²·month). Since this factor is expressed relative to the area, comparability across region is ensured. Its inverse, STe _i , is expressed in m²·month/m³, can be interpreted as the surface-time equivalent required to generate one cubic meter of unused water in this region. The value of AMD_worldavg is the consumption-weighted average of AMD_i over the whole world (0.0136 m³/m²·month). Units of the CF are dimensionless, expressed in m³ _{world eq./}m³ _i(Eq. (3)).

Availability

Actual water availability was obtained from the WaterGAP2.2(Müller Schmied et al. 2014) model for >11,000 watersheds in the world (with the 34 largest watersheds subdivided into sub-watersheds) using climatic data over the period 1960–2010 to model runoff based on precipitation and evapotranspiration. Data are available on a monthly time step and include infrastructure such as dams.

Human demand

Current human water consumption (the fraction of water withdrawal that does not return into the watershed after use) is used to represent human demand, with data obtained from the WaterGAP model (which is based on statistical data for consumption of freshwater withdrawals (Florke et al. 2013). This includes domestic, industrial, agricultural, livestock, and energy production sectors modeled for the year 2010. The WaterGAP consumption data is provided on a scale of 0.5 × 0.5°, worldwide, on an annual time step except for agricultural use which is on a monthly time step.

Ecosystem demand

Environmental water requirements (EWR) for freshwater ecosystems were used as a proxy to represent ecosystem demand. The monthly model from Pastor et al. (2013) is chosen, which was validated with local study cases in five major habitat types encompassing the main freshwater ecoregions. It evaluates minimum water requirements as a fraction of the available flow to maintain freshwater ecosystems in “fair” conditions, with respect to pristine flow (i.e., flow with no human influence), and where “fair” refers to an ecological state of the river between poor and good conditions. The EWR for fair-condition freshwater ecosystems ranges between 30 and 60% of the pristine flow as a function of the seasonal flow patterns (60, 45, and 30% during low flow, intermediate, high flow season, respectively); hence, the underlying assumption is that “fair condition with respect to pristine conditions” already corresponds to the current state of ecosystems, since most rivers are already somewhat degraded when compared without human influence (Smakhtin et al. 2004). Environmental flow requirements were calculated with the monthly natural flow values from WaterGAP, which models the flow without consideration of any human intervention or land use change (i.e., natural vegetation cover). Water requirements of terrestrial and groundwater-dependent ecosystems were not included since the link between blue water consumption (i.e., water abstracted from water bodies, for which AWARE is used) and water deprivation of terrestrial ecosystems is unclear at this time, except for specific cases such as groundwater table lowering or wetlands (van Zelm et al. 2011; Verones et al. 2013). Similarly, green water, or the soil moisture from precipitation, was excluded with a recommendation that it be addressed by a separate indicator assessing green water consumption, linked with land use (Boulay et al. 2015a).

Modeling choices

Additional modeling choices are relevant to the design of this method, namely, (1) span and use of thresholds, (2) normalization with a reference flow, and (3) scaling modeling. The first describes the setting of thresholds, below and above which the value will be set as minimal and maximal. This choice limits the span of the CF to a maximal range that sets the difference between the lowest and highest value to three orders of magnitude, eliminating the tailing values where the meaning of the CF would be lost. Here, cutoff values of 0.1 and 100 are applied (Eq. (4a) and Eq. (4b), see ESM for details). The second choice is the normalization to a reference flow such as the potential impact of world average consumption, or a specific region, following similar reasoning as in global warming potential where CO₂ is taken as a reference flow. Although both differ in the type of reference (a region versus a substance), the role of the reference is to translate an inventory of different flows into an equivalent reference flow. While this choice changes the absolute value of the CF, it does not change the relative results and may enhance the communicability, for example, by providing units of m³-equivalent, i.e., water consumption that are equivalent to the selected reference flow. Normalized CFs facilitate communication on a scale where the value of 1 correspond to the potential impact of the reference flow; values below and above 1 are respectively better and worse than the reference flow. Here, the world average is used as a reference flow (Eq. (3)). The third choice is the use of a scaling function to fit the obtained values within a defined range, such as a logistic curve ranging between 0 and 1 used in previous methods (Pfister et al. 2009; Boulay et al. 2011c). This provided a distribution of values with the hypothesis that impacts have a logistic relationships with the original fraction calculated (WTA, CTA, etc.) and can prevent the use of cutoffs. However, such modeling implies normative choices for the curve tuning parameters and little information is available to support this. For this reason, unlike previous methods, no such additional modeling was performed on the designed method in addition to the choice of cutoffs.

Results

Results are available at www.wulca-waterlca.org and shown in Fig. 2 at the annual level. Curves describing the behavior of the CF in specific watersheds over the year are shown in the Electronic Supplementary Material (ESM; Fig. S5).

$$ \mathrm{Water}\mathrm{Scarcity}\mathrm{Footprint}=\mathrm{Water}\mathrm{consumption}\left(\mathrm{inventory}\right)\times {\mathrm{CF}}_{\mathrm{AWARE}} $$

(5)

Fig. 2

AWARE characterization factors for water scarcity footprint in m³ world eq./m³ consumed in region i (represented at annual level for non-agricultural use, i.e., equal contribution of each month)

Similar to Global Warming Potential (GWP) from IPCC (Myhre et al. 2013), the CF represents a relative value of the impact score of a water consumption in comparison with a reference expressed in terms of m³world eq. per m³ consumed in region i (see Eq. (3)). For the purpose of comparing water consumptions in different regions and months, the units m²·month are considered equivalent everywhere. This assumes that consuming water in two regions with the same amount of regional remaining water per m²·month after human and aquatic ecosystem demands were met is considered equal, as no other regional specification is included.

The CF is limited to a range from 0.1 to 100, with a value of 1 corresponding to a region with the same amount of remaining water per area within a certain period of time as the world average, values <1 for regions with less problems of scarcity than the world average and a value of 10, for example, representing a region where there is 10 times less water remaining per area within a certain period of time as the world average, or that it takes 10 times more surface time to generate an amount of unused water in this region than the world average, assuming a given level of water demand. The effect of the upper and lower limits chosen as cutoffs is documented in Table S2 and S3 in ESM in terms of the fraction of the world water consumption or world area which is affected by the choices, respectively. The upper cutoff of 100 affects regions where demand is higher than availability (representing 33% of world consumption at monthly level) and regions with AMD_i smaller than a 100 times AMD_worldavg (representing 5% of world water consumption). Together (38%), these values are comparable to the maximal values attributed in Boulay et al. (2011b) (also affecting 38% of world water consumption) and Pfister et al. (2009) (30% of world water consumption, for >0.99 of max). The lower cutoff of 0.1 has a negligible effect of less than 1% of world water consumption.

The CF is calculated at the sub-watershed level and monthly time step and available on that scale (see the ESM, Fig. S11 for monthly maps). Values are also aggregated to country level and/or annual time step for use with current inventory data at the respective resolutions. This aggregation can be done in different ways to better represent the time of year and location within the country of an agricultural use or a domestic/industrial use. Country annual average characterization factors for agricultural and non-agricultural use are therefore provided, based on water consumption-weighted averages at monthly and watershed level. The rationale for using country annual averages for agriculture vs non-agricultural users is only relevant when monthly and watershed values cannot be used because of lack of inventory information on the exact month or location of the water consumption. In order to aggregate from a smaller scale (month or sub-watershed) to a larger one (year or country), we need the time and space distribution of the water consumption (available from WaterGAP on the WULCA website). Agricultural water use (for irrigation) will occur more in certain regions and certain months (for example, in summer months for Mediterranean areas), so it is possible to aggregate the values to better represent agricultural use. The same is true for non-agricultural water consumption, although more evenly distributed. It is therefore simply a way to reduce the error from spatial and temporal variability when using large scale aggregated factors.

The resulting characterization factors of the three options discussed above (DTA_A, DTA_X, 1/AMD) are shown in Figs. S1–S3 in the ESM.

Discussion

Modeling

The format and interpretation of this method differ from previous scarcity methods used in LCA (see methods comparison, section V in the ESM). It presents a concept similar to a previous ecosystem assessment characterization method (Pfister et al. 2009), and which is also used in a recently developed scarcity method for water footprint (Yano et al. 2015). However, the previous methods did not account for the water available after deducting current demand. These similarities demonstrate that water use impact assessment methods have evolved in the same direction.

While the AWARE modeling requires an intrinsic cut-off, it does not include additional modeling, such as a logistic curve as done previously in other methods (Pfister et al. 2009; Boulay et al. 2011b; Berger et al. 2014). This avoids the additional arbitrary choice of curve fitting and thresholds (different than cutoffs, discussed below), which were originally used to define water scarcity or stress, based on WTA (Alcamo et al. 2000; Vorosmarty et al. 2000). Since the meaning of this method is chosen to answer an LCA-oriented question “What is the potential to deprive another user when using water in this region?”, no reliable thresholds or definitions exist to justify such modeling with a logistic, or other, function. In addition, when modeling from the original fraction results to an index, the physical meaning is lost and rather adjusted to a perception of what is believed the results should look like. Here, since no such adjustment is performed, a value of 10 directly represents a region where 10 times less water is remaining per unit of surface in comparison to the reference flow, i.e., the world average. It can also be interpreted as a region where 10 times more area time is required to generate the same amount of unused water in comparison to the reference flow. These interpretations are taken as representative of the potential of users to be deprived, once multiplied with the inventory. In the context of water scarcity footprints which are reported in the public domain (e.g., in relation to products or organizational performance), the result has a relatively simple intuitive meaning. Since water scarcity affects some regions more so than others, the results are reported relative to water consumption at the global average location of water consumption.

The CF results present a larger distribution above one than below one (see Fig. 2). This is because the world average is calculated on the AMD_i, whereas the CF is based on the inverse (1/AMD_i), resulting in mathematically more weight being given to smaller values of AMD_i (i.e., larger CF). This results in a larger discriminatory power for regions where AMD_i is lower than AMD_worldavg (and where conversely CF _i is larger), which can be considered desirable since it is in the distinction of most scarce regions that the method is the most useful. These regions are also where the method is the most sensitive to data uncertainty, as discussed below.

Span

The span of this new CF is chosen to be three orders of magnitude, between 0.1 and 100. In previous midpoint methods, this varied from two orders of magnitude (0.01–1) for Pfister et al. (2009) and Berger et al. (2014), and up to 5, 7, and 9 orders of magnitude for Boulay et al. (2011b), Hoekstra et al. (2012), and Swiss Eco-Scarcity method (Frischknecht et al. 2008), respectively, excluding the zero values. This was an important choice which was made with the thresholds placed along the distribution curve in order to keep as much of the natural distribution as possible yet fix the tailing values to the maximum and minimum (see Fig. S4 in ESM). This normative choice of a maximal range of three orders of magnitude was based on expert judgment. The analysis of the preliminary results revealed that three orders of magnitude was comparable to the variation within inventories and therefore meaningful for a balance between LCI and LCIA. Moreover, this range allowed for both the choice of geographical location (i.e., the water scarcity) and the improvement in water efficiency (i.e., the inventory) to play a significant role in the impact score and hence be improved for reducing impacts. This was not the case with a method spreading over four orders of magnitude, as initially considered. Reducing it to two orders of magnitude (cutoff of 10) was also considered but the cutoff affected an additional 17% of the world water consumption, and up to 43% of the world area for at least 1 month (compared to values in the ESM, Tables S2 and S3). This was judged too influential and resulting in too large of a loss of discriminatory power for regions with less than 10 times remaining water than the world average.

Limitations

The quantification of ecosystem demand involves some choices and uncertainty which are inherent to the method chosen (Pastor et al. 2013). State of the art, monthly assessment was used in this method which is based on a fraction of the available flow being reserved for freshwater ecosystems. This approach was thought to be the most robust because it is the only global method that evaluates EWR on a monthly basis validated with several case studies across five different freshwater ecoregions (Pastor et al. 2013). However, there are also some limitations. The EWRs used vary monthly as a function of flow patterns but not as a function of other environmental aspects and the algorithm calculating EWR at global scale does not account for specific local aspects due to limited data access at global scale (river width, global aquatic fauna, etc.). Moreover, although the underpinning data includes information about the location of dams, there is variation and uncertainty about the ways in which these infrastructures are managed. In some cases, the management of dams includes specific water releases to meet environmental flow requirements.

Sensitivity to EWR

Considering the points mentioned above, the sensitivity of the method is tested using 150% of the value of EWR. The resulting values of the factors (of AWARE_EWR150%) show a 97.8% ranking consistency with the original values, using the rank correlation coefficient as in Boulay et al. (2015c). Only 3% of the world area passes beyond point of “demand > availability” on an annual level, corresponding to 10% of the world water consumption when an upper value of EWR150% is used (see Tables S2 and S3 in the ESM).

If another method was selected for the assessment of EWR, such as Richter et al.(2012) allocating 80% of natural flows for environmental requirements at all times, the fraction of the world consumption occurring in regions where “demand > availability” would be 21% (5% of world area) on an annual scale (compared to 3.8 and 0.8%, respectively, with current method) and 50% on a monthly scale (25.5% of area) for at least 1 month (compared to 33 and 12%, respectively with current method). This difference is explained by the fact that the current method does take into account flow seasonality in EWR, which will indeed lower the demand for some months and when compared to an assessment using a constant and maximal fraction of the flow all year round like Richter et al. (2012). Moreover, Richter et al. (2012) only allows 20% of daily flow to be used, which is limited in comparison to actual consumption levels in some regions of the world. As per the authors, this is based on a precautionary approach which is not the reference normally used in LCA. The annual average of Pastor et al. (2013) amounts to approximately half of the 80% value of Richter et al. (2012). This choice was made not only because it is the most recent method but also it introduces the monthly variation of flow requirement and allows a higher discrimination power due to the lower EWR share. This choice of water requirements, describing “fair conditions of ecosystems with respect to pristine environment” (taken as proxy for current state), is, however, different in different methods and based on expert assessment. AWARE therefore sets this proxy for current aquatic ecosystem demand as being equivalent in terms of the definition of demand, to current human water consumption. In reality, humans need more water than just consumption, to make up for withdrawals and uses that are not consumptive, and ecosystems may also use more water if it is available. This choice may be debatable and other approaches could have been used (assessing only essential human water consumption for example, or defining all water availability to ecosystem requirements), but it was judged to be the best considering existing models and data.

Aggregation of CFs

Another important new aspect introduced with this method is the choice of different values at the country and/or annual level, representing different types of aggregation for different uses. This provides an additional level of information in order to better bridge the gap between the spatial and temporal resolutions of the inventory in LCA with the relevant resolutions for water use impact assessment. While data on exact location within a country or exact timing during the year may not be known, the choice of selecting whether the water use is for agricultural purpose or not is already valuable information which can be used to enhance the representativeness of the aggregated CF.

Variability

Temporal

At the watershed level, the difference between monthly and annual values has shown a rank correlation 65–97% (when compared to annual non-agri average) and 67–87% (when compared to agri average), with July being the lowest correlated month, and non-agri year average showing in general a higher correlation. The largest difference between monthly and annual are shown in Figs. S5 and S6 (ESM). About 50% of the world consumption is located in regions where the variation between the most different month (high or low) and the annual value is larger than 50, enforcing the importance of temporal resolution. Differences are especially seen in central Asia, Spain, North and South Africa, Western Australia, Middle East, and parts of China.

Spatial

Spatial variability was analyzed by comparing annual values for each watershed with the annual value for this country. Maps illustrating this difference are shown in the ESM (Figs. S7 and S8). Here, differences are seen in Sub-Saharan Africa, Australia, Central Asia, and USA (specifically for agri CF). Lastly, the rank correlation between agri and non-agri annual values at the annual watershed level showed a rank correlation of 97% and is shown in Fig. S9 (ESM), meaning that although absolute values may differ significantly, the ranking of the watersheds is relatively well maintained. Largest differences are observed in central USA, Chile, Spain, North Africa, and Central Asia.

Uncertainty

Global hydrological models are uncertain, especially at the monthly level (Scherer et al. 2015) and this is propagated to water scarcity measures (Pfister and Hellweg 2011; Núñez et al. 2015; Boulay et al. 2015c). This is mainly affecting not only water availability but also the demand side. Human demand is mainly estimated using model estimates and proxy data, until complete and consistent water consumption data is available worldwide. The point at which demand is higher than renewable availability, and hence the resulting value reaches the limit at which the factor is set to maximal (i.e., 100), is linked to EWR which is the most uncertain value. Due to the nature of the method, the largest differences in absolute terms are seen in regions where demand is close to availability (and the CF is large). For these regions, the relative significance of uncertainty in EWR increases (see example in the ESM, Fig. S13).

No analytical uncertainty propagation is possible due to the discrete steps in the function but stochastic uncertainty assessment should be done in the future. The model relies on inputs which are in turn outputs of models for which uncertainty distributions are not yet provided.

Applicability

As per standard LCA practices, the AWARE factors are meant for use in LCA under the assumption of the marginality of the intervention (i.e., water consumption) in comparison to the background. Further discussion on this can be found in ESM. Regionalized assessment is still a challenge with the current databases and software, but is nonetheless possible. A Simapro-compatible csv file with AWARE CFs at the country level can be downloaded from the WULCA website, and OpenLCA is working on the applicability of regionalized impact assessment with AWARE. Furthermore, while inventory databases do not yet provide completely regionalized data, referring to a “global” region when no geographic information is specified, ecoinvent already focused on introducing the possibility of regionalization of water use flows into version 3 (Pfister et al. 2016).

Conclusions

After 8 years of development, and 2 years of consensus building, AWARE is the new recommended method for assessing impacts from water consumption because of the following: i—it assesses both human and ecosystems users potential deprivation, at the midpoint level; ii—it is based on consensus from LCA and hydrology experts and is recommended by the Life Cycle Initiative, and iii—it is compliant with the LCA-based water footprint standard ISO 14046 to perform a water scarcity footprint (to be complemented with water quality indicators for a comprehensive water footprint). Since not only the nature and model hypothesis are different in AWARE than in previous methods but also the meaning of this method is specifically developed to answer the LCA-oriented question “What is the potential to deprive another user when using water in this region?”, uptake and application of the method by users may reveal different conclusions in future case studies. Although the group reached consensus on this recommendation, it is recommended to use a conceptually different method in parallel for sensitivity studies to test and improve the robustness of the conclusion. There is still a need for further testing on a wider range of case studies.