Skip to main content
SpringerLink
Log in

Toward a solution of allocation in life cycle inventories: the use of least-squares techniques

  • UNCERTAINTIES IN LCA
  • Published:
The International Journal of Life Cycle Assessment Aims and scope Submit manuscript

Abstract

Purpose

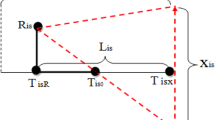
The matrix method for the solution of the so-called inventory problem in LCA generally determines the inventory vector related to a specific system of processes by solving a system of linear equations. The paper proposes a new approach to deal with systems characterized by a rectangular (and thus non-invertible) coefficients matrix. The approach, based on the application of regression techniques, allows solving the system without using computational expedients such as the allocation procedure.

Methods

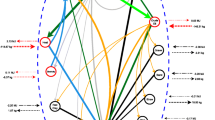
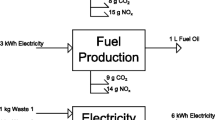
The regression techniques used in the paper are (besides the ordinary least squares, OLS) total least squares (TLS) and data least squares (DLS). In this paper, the authors present the application of TLS and DLS to a case study related to the production of bricks, showing the differences between the results accomplished by the traditional matrix approach and those obtained with these techniques. The system boundaries were chosen such that the resulting technology matrix was not too big and thus easy to display, but at the same time complex enough to provide a valid demonstrative example for analyzing the results of the application of the above-described techniques.

Results and discussion

The results obtained for the case study taken into consideration showed an obvious but not overwhelming difference between the inventory vectors obtained by using the least-squares techniques and those obtained with the solutions based upon allocation. The inventory vectors obtained with the DLS and TLS techniques are closer to those obtained with the physical rather than with the economic allocation. However, this finding most probably cannot be generalized to every inventory problem.

Conclusions

Since the solution of the inventory problem in life cycle inventory (LCI) is not a standard forecasting problem because the real solution (the real inventory vector related to the investigated functional unit) is unknown, we are not able to compute a proper performance indicator for the implemented algorithms. However, considering that the obtained least squares solutions are unique and their differences from the traditional solutions are not overwhelming, this methodology is worthy of further investigation.

Recommendations

In order to make TLS and DLS techniques a valuable alternative to the traditional allocation procedures, there is a need to optimize them for the very particular systems that commonly occur in LCI, i.e., systems with sparse coefficients matrices and a vector of constants whose entries are almost always all null but one. This optimization is crucial for their applicability in the LCI context.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  • Ardente F, Beccali M, Cellura M (2004) F.A.L.C.A.D.E.: a fuzzy software for the energy and environmental balances of products. Ecol Model 176(3–4):359–379

    Article  Google Scholar 

  • Azapagic A, Clift R (1999) Allocation of environmental burdens in multiple-function systems. J of Clean Prod 7:101–119

    Article  Google Scholar 

  • Beghelli S, Guidorzi RP, Soverini U (1987) Structural identification of multivariable systems by the eigenvector method. Int J Control 46:671–678

    Article  Google Scholar 

  • Blunier B, Pucci M, Cirrincione G, Cirrincione M, Miraoui A (2008) A scroll compressor with a high-performance sensorless induction motor drive for the air management of a PEMFC system for automotive applications. IEEE Trans Veh Technol 57(6):3413–3427

    Article  Google Scholar 

  • Cirrincione M, Pucci M, Cirrincione G, Capolino GA (2003) A new experimental application of least-squares techniques for the estimation of the induction motor parameters. IEEE Trans Ind Appl 39(5):1247–1256

    Article  Google Scholar 

  • Cirrincione M, Pucci M, Cirrincione G, Capolino GA (2006) An adaptive speed observer based on a new total least-squares neuron for induction machine drives. IEEE Trans Ind Appl 42(1):89–104

    Article  Google Scholar 

  • Cirrincione M, Pucci M, Cirrincione G, Capolino GA (2007) Sensorless control of induction machines by a new neural algorithm: The TLS EXIN neuron. IEEE Trans Ind Electron 54(1):127–149

    Article  Google Scholar 

  • De Moor B (1990) Total least squares with inequality constraints. ESAT-SISTA Report 1990-02, Department of Electrical Engrg., Katholieke Universiteit Leuven, Leuven, Belgium

  • DeGroat RD, Dowling EM (1993) The data least squares problem and channel equalization. IEEE Trans Signal Process 41(1):407–411

    Article  Google Scholar 

  • Dobson AJ (1983) Introduction to statistical modelling. Chapman and Hall, London

    Google Scholar 

  • Dunne BE, Williamson GA (2003) QR-based TLS and mixed LS–TLS algorithms with applications to adaptive IIR filtering. IEEE Trans Signal Process 51(2):386–394

    Article  Google Scholar 

  • Ekvall T (1994) Principles for allocation at multi-output processes and cascade recycling. In: Huppes G, Schneider F (eds) Proc. of the European Workshop on Allocation in LCA, Leiden, February 1994. SETAC-Europe, Brussels, pp 91–101

  • Fisher GW (1989) Matrix analysis of metamorphic mineral assemblages and reactions. Contrib Mineralogy Petrol 102:69–77

    Article  CAS  Google Scholar 

  • Golub GH, Van Loan CF (1980) An analysis of the total least squares problem. SIAM J Numer Anal 17:883–893

    Article  Google Scholar 

  • Golub GH, van Loan CF (1989) Matrix computations. John Hopkins University Press, 2nd ed., 1989

  • Guinée JB, Heijungs R, Huppes G (2004) Economic allocation: examples and derived decision tree. Int J Life Cycle Assess 9(1):23–33

    Article  Google Scholar 

  • Hall HR, Bernhard RJ (1989) Total least squares solutions to acoustic boundary element models, In Proc. Internat. Symposium on Numerical Techniques in Acoustic Radiation, ASME Winter Annual Meeting, San Francisco, CA,1989, R.J. Bernhard and R.F. Keltie (eds.), American Society of Mechanical Engineers, New York, 1989, NCA (6):145-152

  • Harville DA (1997) Matrix algebra from a statistician’s perspective. Springer, New York

    Google Scholar 

  • Heijungs R (1994) The problem of allocation: some more complications. In: Huppes G, Schneider F (eds) Allocation in LCA. SETAC-Europe, Brussels, pp 8–12

    Google Scholar 

  • Heijungs R, Frischknecht R (1998) A special view on the nature of the allocation problem. Int J Life Cycle Assess 3(5):321–332

    Article  Google Scholar 

  • Heijungs R, Suh S (2002) The computational structure of life cycle assessment. Kluwer Academic Publishers, Dordrecht. Series: Eco-Efficiency in Industry and Science, vol. 11

  • Heintz B, Baisnee PF (1992) System boundaries. In: Life cycle assessment, SETAC-Europe, Brussels, pp 35–52

  • International Standard ISO 14044 (2006) Environmental management—life cycle assessment—requirements and guidelines

  • Jakubek S, Hametner C, Keuth N (2008) Total least squares in fuzzy system identification: an application to an industrial engine. Eng Appl Artif Intell 21:1277–1288

    Article  Google Scholar 

  • Justice JH, Vassiliou AA (1990) Diffraction termography for geophysical monitoring of hydrocarbon reservoirs. Proc IEEE 78:711–722

    Article  CAS  Google Scholar 

  • Klöpffer W, Rebitzer G (2000) A report on LCA activities at the SETAC—Third World Congress, 21–25 May 2000 in Brighton UK. Int J Life Cycle Assess 5:249

    Article  Google Scholar 

  • Levin MJ (1964) Estimation of a system pulse transfer function in the presence of noise. IEEE Trans Autom Control 9:229–235

    Article  Google Scholar 

  • Li C, Yu J (2008) Volterra-TLS method for chaotic time series prediction. In: International Conference on Communications, Circuits and Systems. Fujian, China, 25-27 May, pp 48-51

  • Lim JS (2008) Recursive DLS solution for extreme learning machine-based channel equalizer. Neurocomputing 71:592–599

    Article  Google Scholar 

  • Marković D, Jukić D (2010) On nonlinear weighted total least squares parameter estimation problem for the three-parameter Weibull density. Appl Math Model 34:1839–1848

    Article  Google Scholar 

  • Markovsky I, Van Huffel S (2007) Overview of total least squares methods. Signal Process 87(10):2283–2302

    Article  Google Scholar 

  • Mendel JM (1987) Lessons in digital estimation theory. Prentice-Hall, Englewood Cliffs, USA

    Google Scholar 

  • Moonen M, Vandewalle J (1990) A QSVD approach to on- and off-line state-space identification. Int J Control 51:1133–1146

    Article  Google Scholar 

  • Moonen M, De Moor B, Vanderberghe L, Vandewalle J (1989) On- and off-line identification of linear state-space models. Int J Control 49:219–232

    Google Scholar 

  • Paige CC, Strakos Z (2002) Unifying least squares, total least squares and data least squares. In: Van Huffel S, Lemmerling P (eds) Total least squares and errors-in-variables modeling. Kluwer Academic Publishers, Dordrecht, pp 25–34

    Google Scholar 

  • Penrose R (1956) On best approximate solution of linear matrix equations. Proc Camb Philos Soc 52:17–19

    Article  Google Scholar 

  • Rahman MA, Yu KB (1987) Total least squares approach for frequency estimation using linear prediction. IEEE Trans Acoust Speech Signal Process 35:1440–1454, ASSP

    Article  Google Scholar 

  • Ramos JA (2007) Applications of TLS and related methods in the environmental sciences. Comput Stat Data Anal 52:1234–1267

    Article  Google Scholar 

  • Rao BD (1997) Unified treatment of LS, TLS and truncated SVD methods using a weighted TLS framework. In: Van Huffel S (ed) Recent advances in total least squares techniques and errors-in-variables modelling. SIAM Publications, Philadelphia, pp 11–20

    Google Scholar 

  • Rost RW, Leuridan J (1985) A Comparison of least squares and total least squares for multiple input estimation of frequency response functions, ASME Paper Number 85-DET-105, presented at the ASME Design Engineering Division Conference and Exhibit on Mechanical Vibration and Noise, Cincinnati, OH

  • Roy R, Kailath T (1987) Total least-squares ESPRIT, Proc. 21st Ann. Asilomar Conf. On Signals, Systems and Computers, Pacific Grove, CA, pp 297-301

  • Roy R, Kailath T (1989) ESPRIT—estimation of signal parameters via rotational invariance techniques. IEEE Trans Speech Signal Process 37(7):984–995

    Article  Google Scholar 

  • Silvia MT, Tacker EC (1982) Regularization of Marchenko's integral equation by total least squares. J Acoust Soc Am 72:1202–1207

    Article  Google Scholar 

  • Stewart GW, Sun J (1990) Matrix perturbation theory. Academic Press, Inc., Boston

    Google Scholar 

  • Stoian A, Stoica P, Van Huffel S (1990) Comparative performance study of least-squares and total least squares Yule-Walker estimates of autoregressive parameters. Scientific Bulletin, Electrical Eng Series, Polytechnic Institute of Bucharest 52(2):81–89

    Google Scholar 

  • Swindlehurst AL, Ottersten B, Roy R, Kailath T (1992) Multiple invariant ESPRIT. IEEE Trans Signal Process 40(4):867–881

    Article  Google Scholar 

  • Tillman AM, Ekvall T, Baumann H, Rydberg T (1994) Choice of system boundaries in life cycle assessment. J Clean Prod 2(1):21–29

    Article  Google Scholar 

  • Van Huffel S (1987) Analysis of the total least squares problem and its use in parameter estimation. Doctoral dissertation, Dept. of Electr. Eng., Katholieke Universiteit Leuven

  • Van Huffel S, Vandewalle J (1988) Analysis and solution of the nongeneric total least squares problem. SIAM J Matrix Anal Appl 9:360–372

    Article  Google Scholar 

  • Van Huffel S, Vandewalle J (1989) Algebraic connections between the least squares and total least squares problems. Numer Math 55:431–449

    Article  Google Scholar 

  • Van Huffel S, Vandewalle J (1991) The total least squares problems: computational aspects and analysis. Frontiers in Applied Mathematics, SIAM Philadelphia

    Google Scholar 

  • Van Huffel S, Vandewalle J, De Roo MC, Willems JL (1987) Reliable and efficient deconvolution technique based on total linear least squares for calculating the renal retention function. Med Biol Eng Comput 25:23–33

    Article  Google Scholar 

  • Zoltowski MD (1987) Signal processing applications of the method of total least squares with applications to array processing, In Proc. 21st Asilomar Conf. On Signals, Systems and Computers, Pacific Grove, CA, pp 290-296

  • Zoltowski MD (1988) Generalized minimum norm and constrained total least squares with applications to array processing, In Proc. SPIE, Advanced Algorithms and Architectures for Signal Processing, III, San Diego, CA 975:78-85

  • Zoltowski MD, Stavrinides D (1989) Sensor array signal processing via a Procrustes rotations based eigenanalysis of the ESPRIT data pencil. IEEE Trans Acoustic Speech Signal Process 37:832–861, ASSP

    Article  Google Scholar 

Download references

Acknowledgment

This work has been carried out with support from (1) the GENIUS LOCI project titled “The role of the building sector on climate change”, funded by the Italian Ministries of Economy; Education; University and Research, Environment and Territory protection, Agricultural and Forestry policies; (2) the Teaching Staff mobility funds in the framework of the LLP/Erasmus program, under the Erasmus Bilateral Agreement in force between the University of Palermo and the University of Leiden.

Author information

Authors and Affiliations

  1. Cork Constraint Computation Centre (4C), University College Cork, Western Gateway Building, Cork, Ireland

    Antonino Marvuglia

  2. Dipartimento di Ricerche Energetiche ed Ambientali (DREAM), Università degli Studi di Palermo, Viale delle Scienze, 90128, Palermo, Italy

    Maurizio Cellura

  3. Institute of Environmental Sciences, Leiden University, P.O. Box 9518, 2300, RA, Leiden, The Netherlands

    Reinout Heijungs

Authors
  1. Antonino Marvuglia
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Maurizio Cellura
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Reinout Heijungs
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Antonino Marvuglia.

Additional information

Responsible editor: Andreas Ciroth

Electronic supplementary materials

Below is the link to the electronic supplementary material.

Appendix

(PDF 67 kb)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Marvuglia, A., Cellura, M. & Heijungs, R. Toward a solution of allocation in life cycle inventories: the use of least-squares techniques. Int J Life Cycle Assess 15, 1020–1040 (2010). https://doi.org/10.1007/s11367-010-0214-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11367-010-0214-1

Keywords

Search

Navigation